
흔히 하는 착각
간혹 모델의 하이퍼파라미터를 튜닝하다 보면 모델의 Accuracy가 높아졌는데 Loss가 커지는 경우, 또는 Accuracy가 낮아졌는데 Loss는 작아지는 경우가 더러 발생한다.
보통 정확도가 높으면 오차도 작을 것이라고 생각할 수 있지만 꼭 그렇지만은 않다.
예시
아래의 표를 보자.
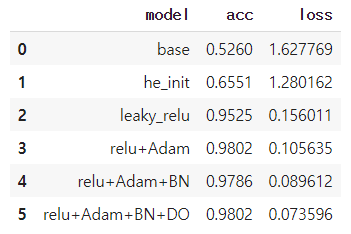
표는 임의의 모델의 성능을 높이기 위해 여러 하이퍼파라미터들을 튜닝하며 각각의 모델의 테스트 정확도와 테스트 오차를 나타낸 것이다. 위에서부터 점점 모델의 성능이 발전하는 것을 알 수 있다.
표의 0번째 행의 base 모델은 성능 상관없이 간편하게 만들었다. 그 다음 모델은 he initialization 가중치 초기화 전략을 적용한 것이고, 그 다음 모델은 활성화 함수를 LeakyReLU로 수정, 그 다음은 활성화 함수는 relu로 하고 optimizer를 Adam으로 수정, 그 다음은 BatchNormalization 추가, 마지막은 Dropout 추가한 것이다.
Base model에서 시작해서 점점 추가해 나간 것이고 모델의 성능도 점진적으로 거의 증가한다.
그럼 본론으로 다시 돌아가서 (꼭 그런 것은 아니지만) 보통 모델의 성능을 평가할 때 Accuracy와 Loss 값을 확인한다. 그런데 3번째 행의 모델과 4번째 행의 모델을 보면 테스트 정확도는 0.9802에서 0.9786으로 떨어졌지만 오차(또는 손실)는 0.105646에서 0.089612로 줄었다. 이것을 보고 바로 정확도와 오차 값의 상관관계는 그다지 크지 않다는 것을 눈치채야 한다.
결론
결론을 말하자면 Loss와 Accuracy는 서로 관련이 없다.
정확도(Accuracy)는 전체 데이터에 대한 예측 오류의 수로 볼 수 있다. 쉽게 말해, 전체 데이터 중에서 몇 개를 맞췄는가이다. 100개 중 97개를 맞췄다면 accuracy는 97%이다.
손실(Loss)은 실제 정답과 모델이 예측 한 값 사이의 차이(거리 또는 오차)이다. 즉, 손실이 클수록 데이터에 대한 오류도 커진다. 쉽게 말해, 틀리게 예측한 경우 얼마나 오류를 범했는가로 볼 수 있다. 따라서 2개의 모델이 100개 중 97개를 똑같이 맞춰도 둘의 오차는 다를 수 있다.
위의 4번째 모델(정확도: 0.9786, 손실: 0.089612)과 비교해서 3번째 모델은(정확도: 0.9802, 손실: 0.105635) 정확도가 높지만(더 많이 맞췄지만) 몇 개의 데이터에서 큰 오류를 범했다고 볼 수 있다.
반대로 3번째 모델과 비교해서 4번째 모델은 정확도가 낮지만 손실이 적다. 즉, 많은 데이터에서 오류가 거의 발생하지 않음을 의미한다.