Bias and Variance Trade-Off

Bias and Variance Trade-Off에 대해 설명하기 전에, Bias와 Variance에 대한 것을 먼저 알아야 합니다.

Bias (편향): 예측 값의 평균 - 실제 값

Variance (분산): 평균에서 얼마나 멀리 분포하는지에 대한 지표

Regression에서의 손실함수 MSE에서 위의 관계를 살펴볼 수 있음.

• MSE: $\frac{1}{n}\sum_{i=1}^n (\hat{\theta}-\theta)^2$

  ->정리하게 되면

MSE: $\frac{1}{n}\sum_{i=1}^n (\hat{\theta}-\theta)^2$

= $E_{\theta}((\hat{\theta}-\theta)^2)$

= $E((\hat{\theta} - E(\hat{\theta}))^2) + (E(\hat{\theta})-\theta)^2$가 된 다.

이때 $E((\hat{\theta} - E(\hat{\theta}))^2) = Var(\hat{\theta})$

그리고 $(E(\hat{\theta})-\theta)^2 = Bias(\hat{\theta}, \theta)^2$이다.

-> 따라서 Bias 값이 낮으면 Var 값이 높고, Bias 값이 높으면 Var 값이 낮다.

Complexity와 Bias, Variance, MSE

• 복잡도가 낮을수록 y 값을 표현하는 변수의 자유도가 낮으므로 bias는 높고, 이에 따라 값의 분포가 모여있게 된다. 따라서 variance는 낮아지게 된다.
• 반대로 복잡도가 높을 수록, 데이터를 더욱 자세하게 표현할 수 있으므로 실제 예측값과 예측값의 평균의 차이가 얼마 나지 않으므로 Bias는 낮아지고, 이에 따라 값의 분포가 커지게 되므로 Variance 값은 커지게 된다.
• 이를 Bias and Variance Trade-Off 라고 한다.

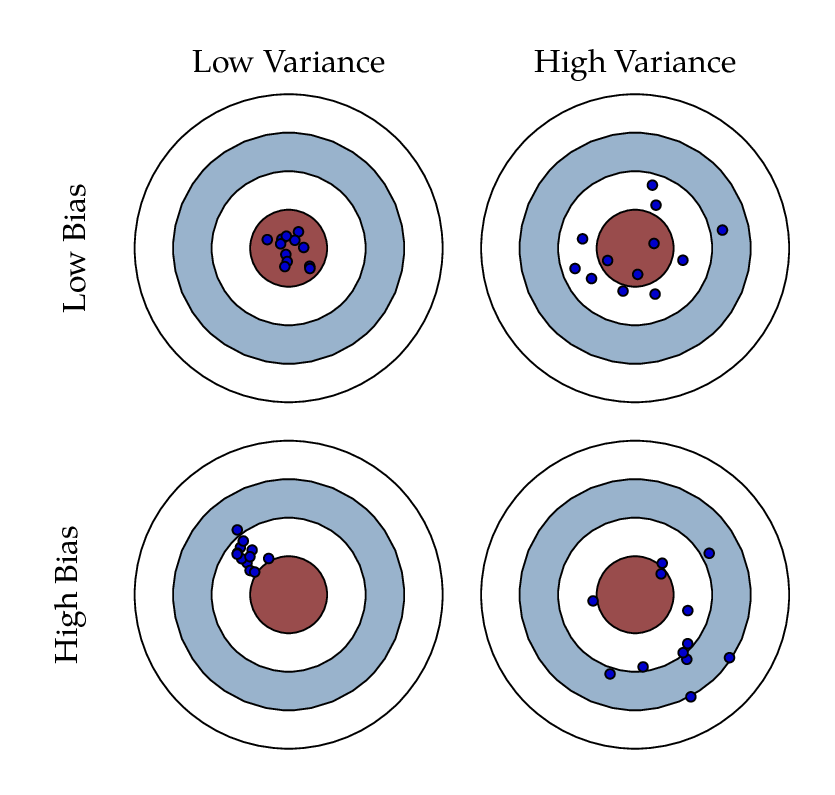
• 위 그림에서 Bias가 작을 땐 실제 예측 값 (가운데 빨간 원)과의 차이가 얼마 안 난다.
• 반대로 Bias가 클 땐 실제 예측 값과의 차이가 있다.
• Variance의 값이 작으면 데이터의 분포 자체가 모여있다.
• Variance의 값이 크면 데이터가 퍼져있다.

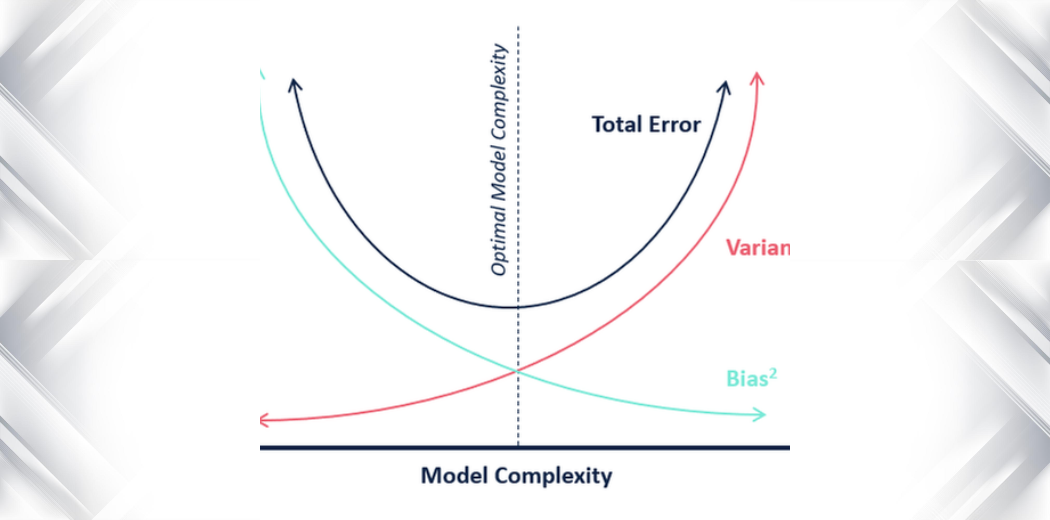
• 모델의 복잡도가 낮아질 땐 데이터에 대한 정확한 표현이 제한되므로 실제 예측값과의 차이가 크기 때문에 Bias는 커지고, 이에 따라 값이 모여있으므로 Variance는 작아지게 된다.
• 반대로 복잡도가 커지면 데이터에 대한 정확한 표현이 가능해지므로 실제 예측값과의 차이가 줄어들기 때문에 Bias는 작아지고, 이에 따라 실제 분포대로 값이 퍼져나가게 되므로 Variance는 커지게 된다.