AI 대학원 면접 준비

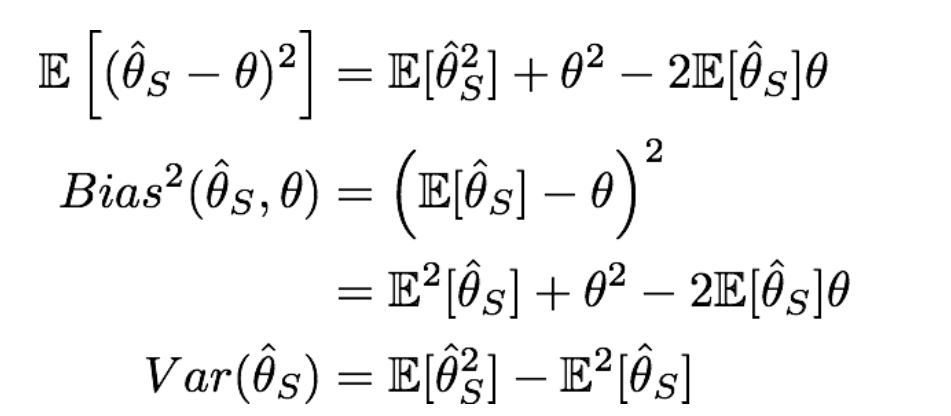
이 질문들의 출처는 https://jrc-park.tistory.com/259 입니다!🧐 Central Limit Theorem 이란 무엇인가?🧐 Central Limit Theorem은 어디에 쓸 수 있는가?🧐 큰수의 법칙이란?🧐 확률이랑 통계랑 다른

중심 극한 정리를 알기 전에, 표본분포에 관련된 내용을 알아야 합니다.모집단에서 일정한 크기로 뽑을 수 있는 표본을 모두 뽑았을 때, 그 모든 표본의 통계량의 확률 분포표본평균$$X_1,..., X_n$$이 모평균(샘플 전체의 평균) $$\\mu$$, 모표준편차 (샘플

확률 변수 X의 값이 0 혹은 1인 분포$$P(x=1): \\mu$$$$P(x=0): 1-\\mu$$ $$P(x | \\mu) = \\mu^x (1-\\mu)^{1-x}$$$$E(x) = \\mu$$$$Var(x) = \\mu(1-\\mu)$$\-> 평균과 분산의 경우

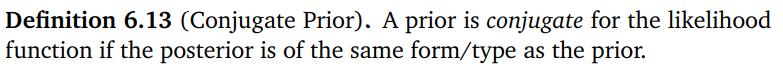
Conjugate Prior는 베이즈 정리를 통해 얻은 poterior, likelihood, prior의 관계를 표현할 때 사용하는 정의이다.$$P(x|y) = \\frac{P(y|x)P(x)}{P(y)}$$ 일때$$P(x|y)$$: posterior$$P(y|x)$

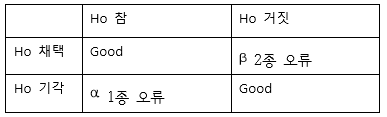
설정한 가설이 옳을 때 표본에서의 통계량과 통계량의 분포에서 이론적으로 얻는 특정 값을 비교하여 가설의 기각/채택 여부를 판정하는 방법.확률적 오차 범위를 넘어서면 가설을 기각한다.유의수준 ($$\\alpha$$): 기각/채택 여부의 판단 기준1) 귀무가설(H0)대립가

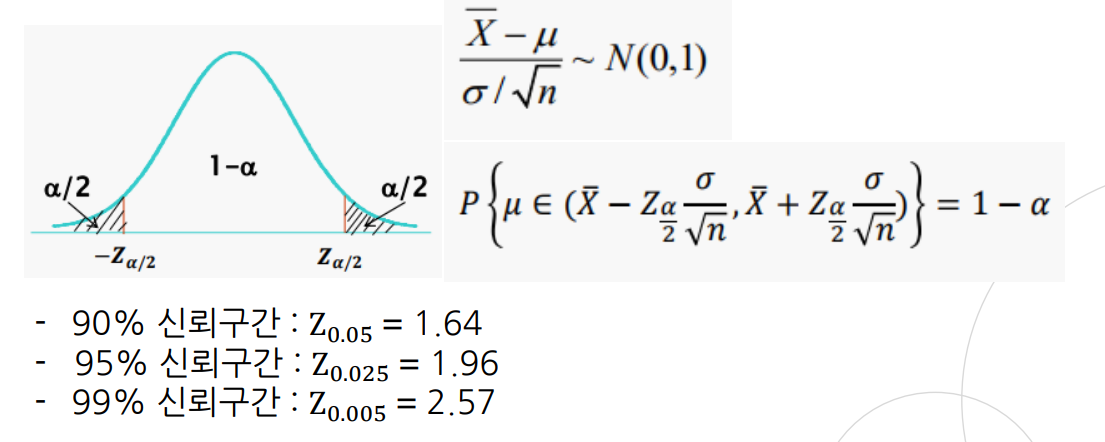
모집단의 모수를 표본으로부터 추정하는 과정점추정 및 구간 추정이 있다.모수를 단일한 값으로 추측하는 방식신뢰도를 나타낼 수 없음모수를 포함한다고 추정되는 구간을 구하는 방식신뢰도를 나타낼 수 있음신뢰구간(Confidence Interval): 모수가 속할 것으로 기대되

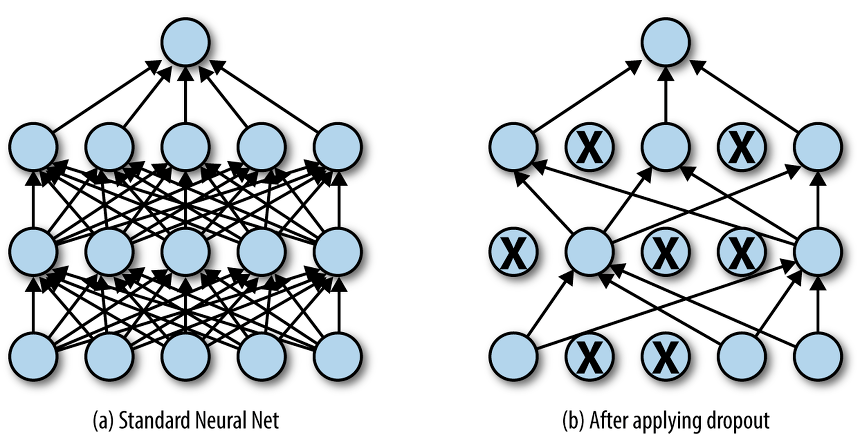
Activation Function (활성 함수): transfer function에서 전달받은 값을 non-linear하게 변화시켜주는 함수.이를 통해 더욱 깊게 Neural Net을 쌓을 수 있게 된다.Linear하게 네트워크가 형성되면 a(a(ax+b)+b)+b

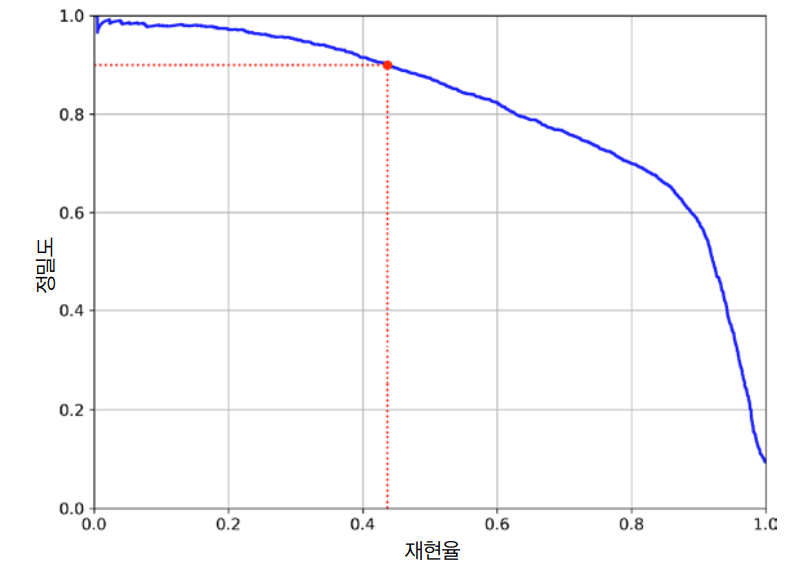
: "아 그 분류기가 맛있다고 추천한 음식중에서 진짜 내가 좋아하는 음식의 비율을 알아보고 싶은데... Precision 지표를 보면 되겠구나": "저 분류기가 내가 좋아하는 것에다가는 True 값을 반환했고, 내가 싫어하는 것은 False 라고 했네?? 저 중에서 내

Receiver Operating Characteristic Curve (ROC Curve) : x축이 FPR, y축이 TPR인 곡선 FPR(False Positive Rate): $$\frac{FP}{FP+TN}$$ = 1-TNR = $$1-\frac{TN}{FP+

: 발생 빈도가 낮은 사건의 단위 당 발생수에 대한 확률 모델$$\\text {subject to } x=0,1,2,...\\text{ and } 0<\\lambda<\\infin$$$$\\lambda=$$ 단위 시간당 평균 발생 횟수기대값: $$

감마 분포를 알기 전에, 감마함수에 대해 알아야 합니다. > ### Gamma Function (감마함수) : 팩토리얼의 일반 버전 $$\Gamma(t+1) = \int_0^\infin x^{t+1}e^{-x} dx$$ $$\Gamma(t+1) = t\Gamma(t)

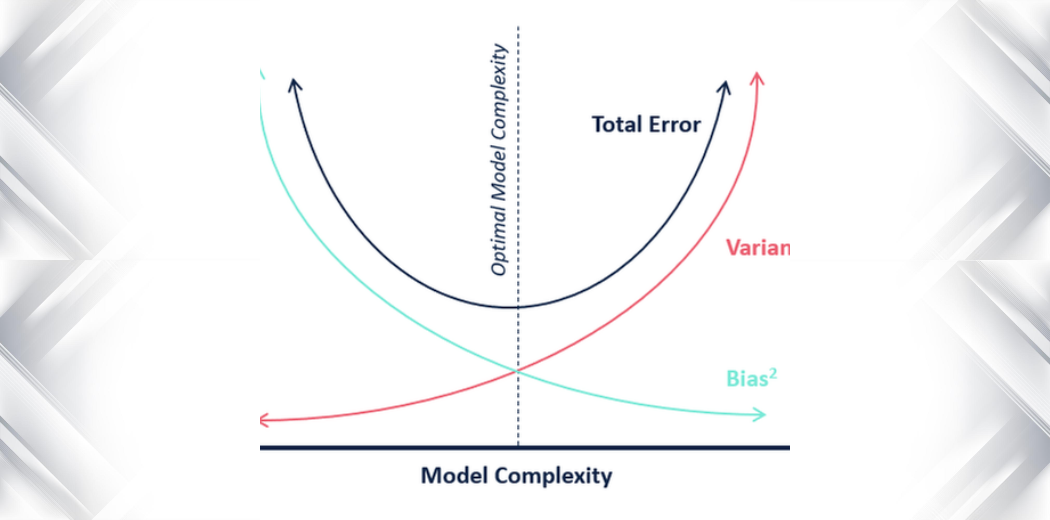
Bias and Variance Trade-Off에 대해 설명하기 전에, Bias와 Variance에 대한 것을 먼저 알아야 합니다. \->정리하게 되면 복잡도가 낮을수록 y 값을 표현하는 변수의 자유도가 낮으므로 bias는 높고, 이에 따라 값의 분포가 모여있게 된다

Linearly Independent란? Vector의 집합 $$V$$ = { $$v1, v2, ..., vn$$}에 대하여 $$c1v1 + c2v2+...+cnvn = 0$$을 만족하는 경우가 $$c1 = c2 = ... = cn = 0$$ 일 때를 의미한다. 즉 집합 $$V$$에 속하는 벡터들의 일차결합 (linear combination)으로는 집합 ...

즉, 표본 평균($$\\bar{X}$$)의 평균은 모집단의 평균인 모평균과 같다.이때 $$Xi -\\bar{X}$$는 편차 (Bias)라 불리고, 편차의 합은 0이된다. $$\\sum{i=1}^N(X_i-\\bar{X}) = 0$$또한 표본 분산의 기대값 $$E(S^2

Bagging Bagging: Bootstrap aggregating의 줄임말 Bootstraping: 복원 추출로 데이터셋을 샘플링하는 방법. Pasting 비복원 추출로 데이터셋을 샘플링하여, 중복되지 않은 데이터로 학습. 사실 Bagging, Pasting은

Sample point (x,y)에 대하여 $$\\hat{y}$$는 $$y$$의 prediction 값이고, $$\\bar{y}$$는 $$y$$의 평균이라 한다.$$\\hat{y}$$ = Prediction of $$y$$$$\\bar{y}$$ = Mean of $$y