Gamma Distribution (감마 분포)

감마 분포를 알기 전에, 감마함수에 대해 알아야 합니다.

Gamma Function (감마함수)

: 팩토리얼의 일반 버전

• $\Gamma(t+1) = \int_0^\infin x^{t+1}e^{-x} dx$
• $\Gamma(t+1) = t\Gamma(t)$

Gamma Distribution (감마 분포)

: $\alpha$번째 사건이 일어날 때까지 걸리는 시간에 대한 분포 ($\beta$: 사건 사이의 평균 소요시간)

$P(x |\alpha, \beta) = \frac{1}{\beta^\alpha\Gamma(\alpha)}x^{\alpha-1}e^{-\frac{x}{\beta}}$, when $x > 0$
$P(x |\alpha, \beta) = 0$, when $x<=0$
$E(X) = \alpha\beta$
$Var(X) = \alpha\beta^2$

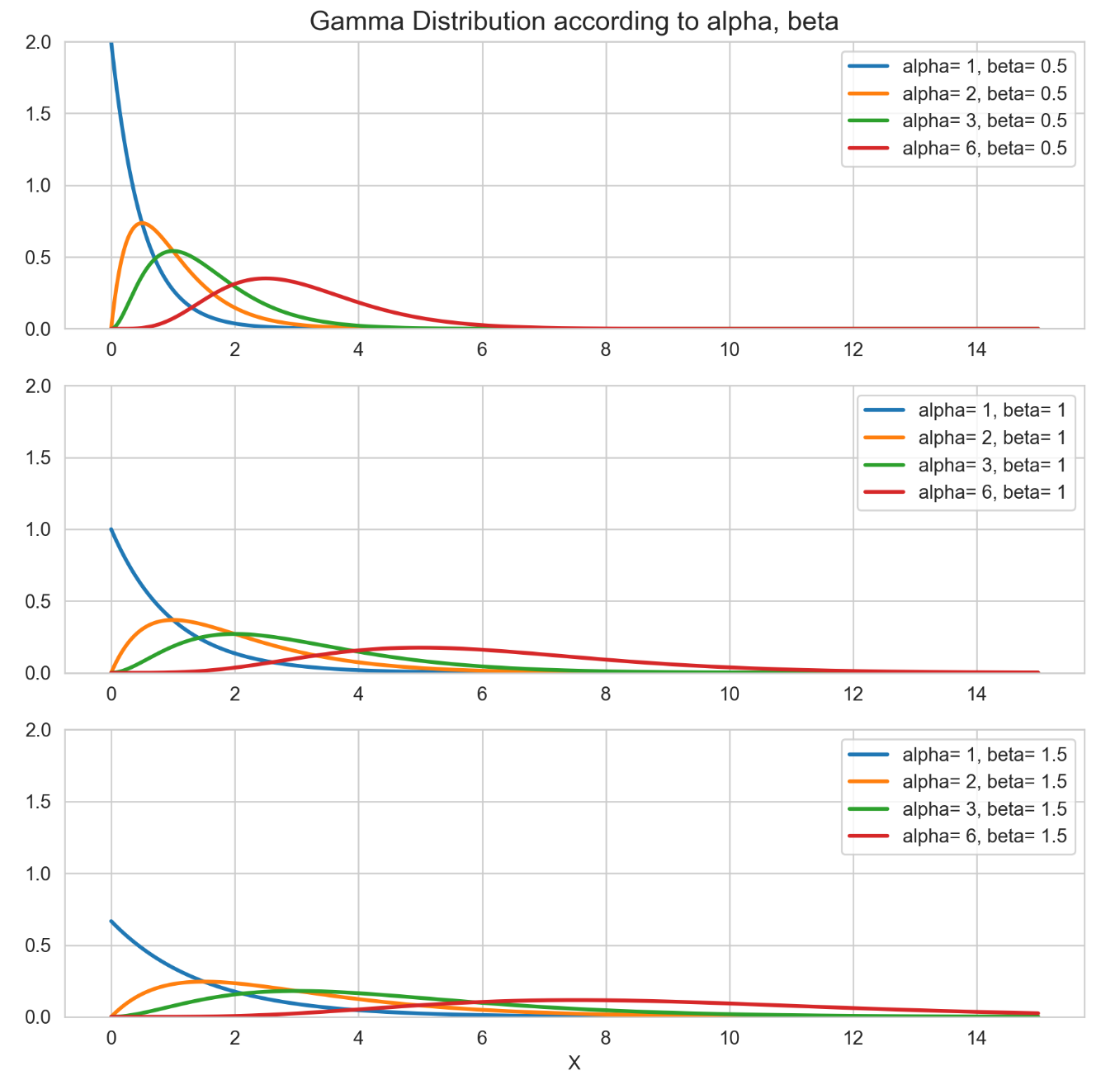
아래는 $\alpha, \beta$값에 따른 분포도입니다.

• $β$ 가 고정되어 있는 상태에서 $α$가 증가할수록 평균과 분산이 커지면서 점점 오른쪽으로 퍼지는 형태라는 것을 알 수 있습니다.
• 이 때, $β$를 증가하면 증가할수록 이 경향은 심해집니다. $β$가 증가할수록 분산이 훨씬 커지게 되어 더욱 퍼지는 형태가 된다는 것을 확인할 수 있습니다.
• 직관적으로도 기다릴 사건 개수($α$)가 많아질수록, 사건 사이 평균 소요시간($β$)이 커질수록 전체 대기 시간이 길어질 것입니다.
  

참고: https://soohee410.github.io/gamma_dist