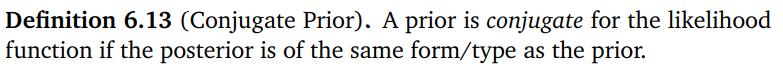
Conjugate Prior는 베이즈 정리를 통해 얻은 posterior, likelihood, prior의 관계를 표현할 때 사용하는 정의이다.

$P(x|y) = \frac{P(y|x)P(x)}{P(y)}$ 일때

• $P(x|y)$: posterior
• $P(y|x)$: likelihood
• $P(x)$: prior

수식에 의해 Posterior는 likelihood와 proir의 곱에 비례한다.

• 이때 likelihood에 대하여 prior와 posterior가 같은 form/type일 때 해당 prior를 conjugate prior라고 한다.
• 즉 사전 확률 (prior)과 사후 확률 (posterior)이 동일한 유형/형태일 경우 사전확률은 우도함수에 대해 쌍을 이룬다라고 표현할 수 있습니다.

-------------------예시-------------------

Beta-Binomial Conjugacy

• 위 관계에서 beta 확률 분포와 binomial 확률 분포는 서로 동일한 형태의 모양을 갖기 때문에 conjugacy입니다.

Beta-Bernoulli Conjugacy

• 위 관계에서 beta 확률 분포와 bernoulli 확률 분포는 서로 동일한 형태의 모양을 갖기 때문에 conjugacy입니다.

참고

Beta Distribution (베타 분포)

• $\alpha, \beta$ 값이 주어지고, 연속 확률 변수 $\mu\in[0,1]$일 때,
• $P(\mu|\alpha,\beta) = \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\mu^{\alpha-1}(1-\mu)^{\beta-1}$의 분포를 갖게되는 것.
• 이때 감마함수는 $\Gamma(t+1)=\int_0^{\infin}x^{t}e^{-x}dx$ 로 정의됨.