[CrashCourse CS] #3 Boolean Logic & Logic Gates

Binary

• Information can be represented just with two states of electricity - we call this representaion "Binary", meaning "of two states"
  • on - electricity flowing - true
  • off - no electricity flowing - false

• Some early electronic computers were ternary(3 states), and even quinary(5 states)
  • Problem: the more intermediate states there are, the harder it is to keep them all seperate.
  • Placing two signals as far apart as possible ("on" and "off") gives the most distinct signal to minimize these issues.
• Another reason that computers use binary - Boolean Algebra already existed in mathmatics.

George Boole

• a self-taught English mathematician in the 1800s.

• He was interested in representing logical statements that went "under, over, and beyond" Aristotles approach to logic.
• Boole's approach allowed truth to be systematically and fomally proven through logic equations.
• Boolean Algebra - values of variables are true and false, and the operations are logical.
• 3 fundamental operations in Boolean Algebra : NOT, AND, OR
  
  

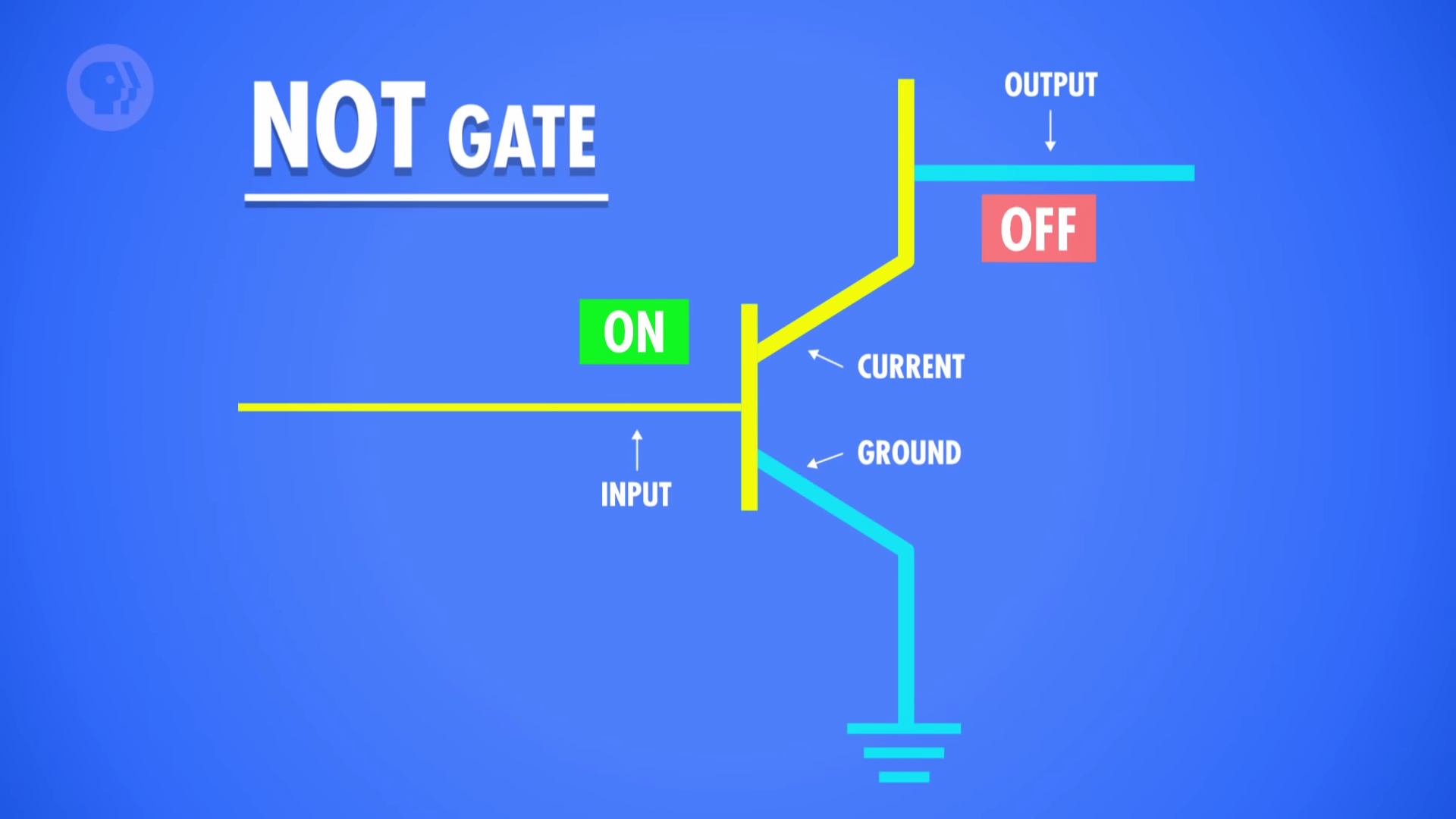
NOT

• Flips true to false, false to true.

Input	Output
TRUE	FALSE
FALSE	TRUE

• NOT gate circuit
  
  
  

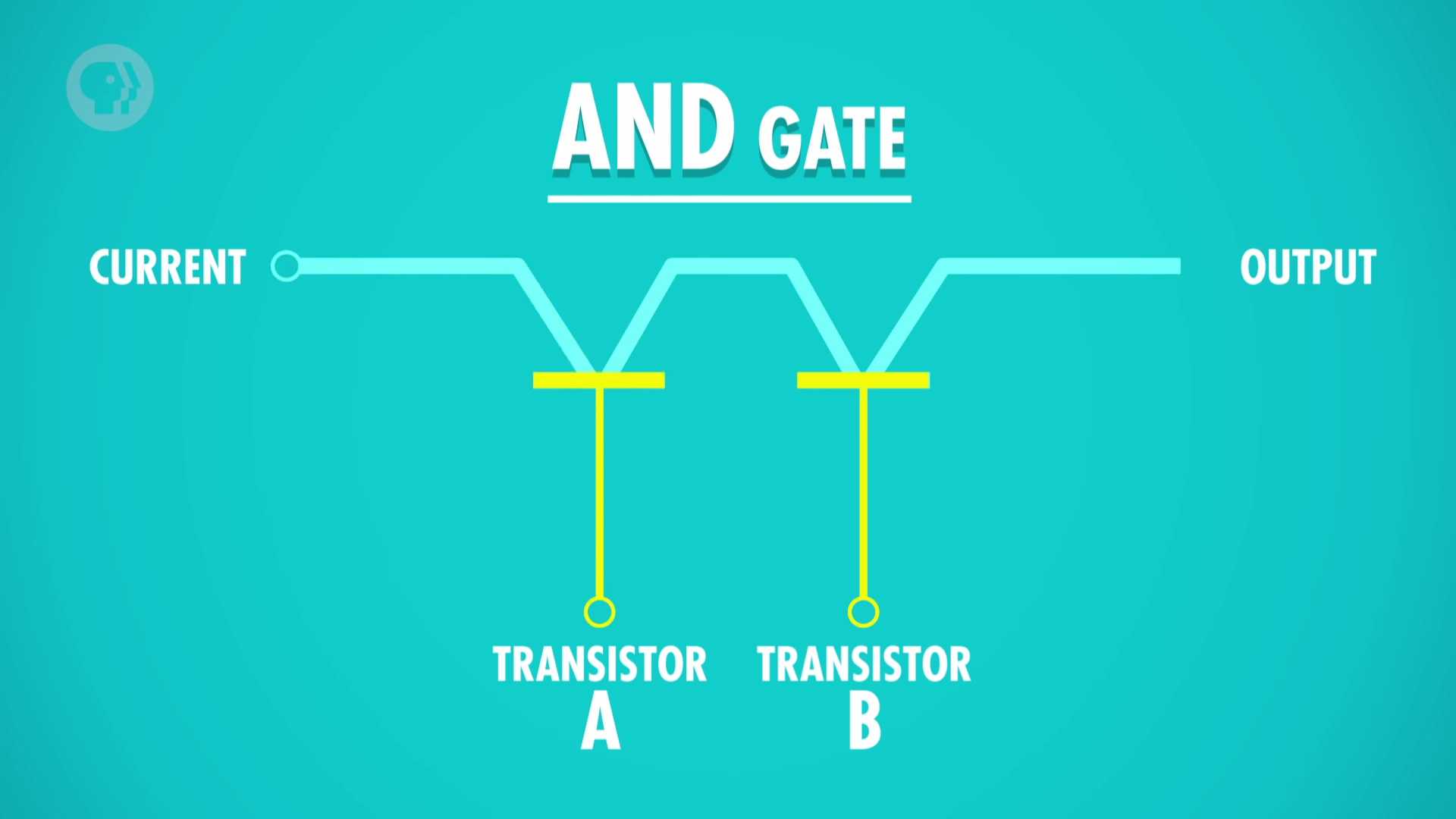
AND

• 2 inputs, 1 output. Ouput is only true if both inputs are true.

Input A	Input B	Output
TRUE	TRUE	TRUE
TRUE	FALSE	FALSE
FALSE	TRUE	FALSE
FALSE	FALSE	FALSE

• AND gate circuit
  
  
  

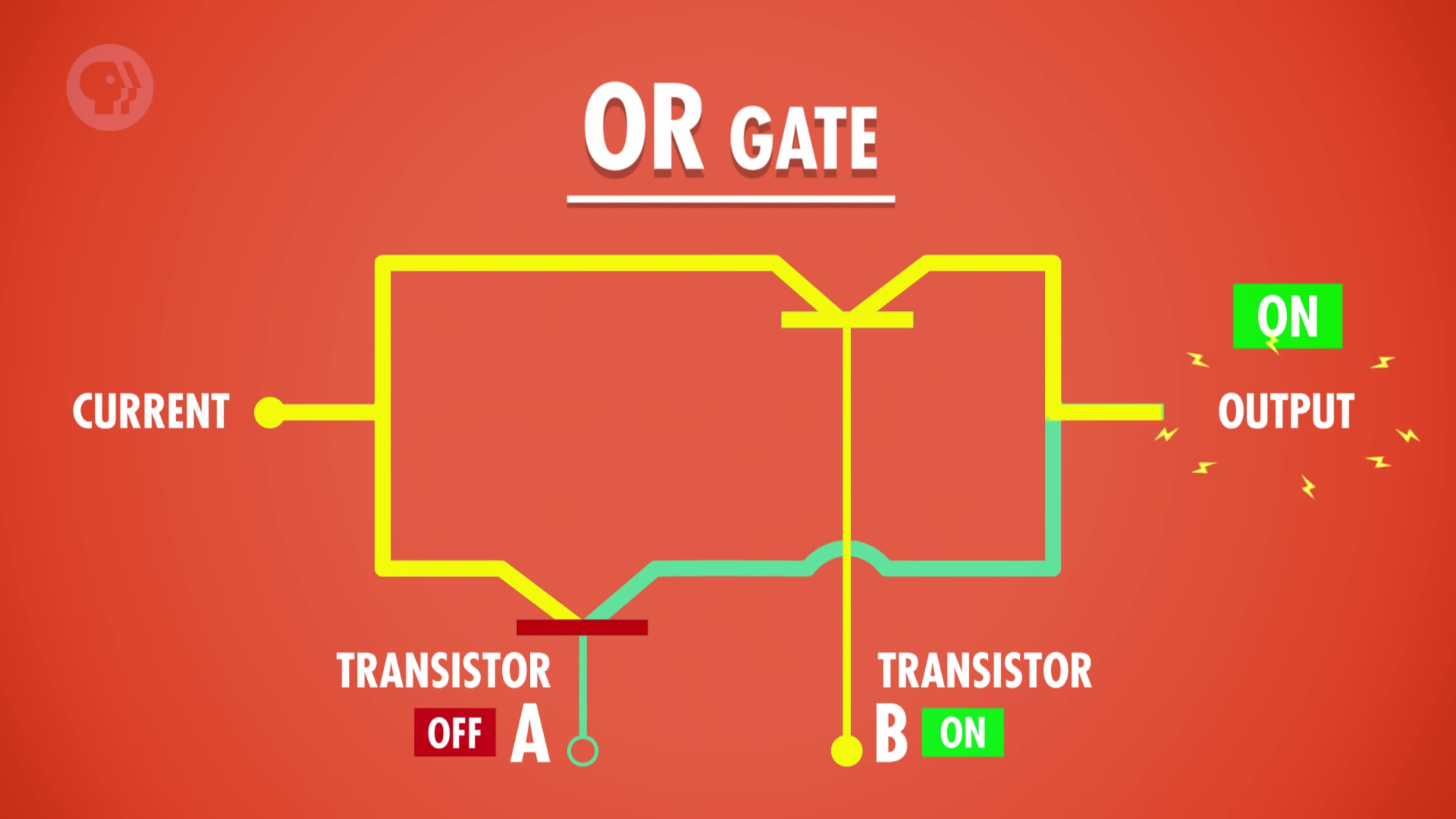
OR

• Only one input has to be true for the output to be true.

Input A	InputB	Output
TRUE	TRUE	TRUE
TRUE	FALSE	TRUE
FALSE	TRUE	TRUE
FALSE	FALSE	FALSE

• OR gate circuit
  
  
  

XOR (Exclusive OR)

• Just like OR, except when both inputs are true, output is false.
• Inputs same : false, inputs different : true.

Input A	Input B	Output
TRUE	TRUE	FALSE
TRUE	FALSE	TRUE
FALSE	TRUE	TRUE
FALSE	FALSE	FALSE

• XOR gate circuit
  
  
  

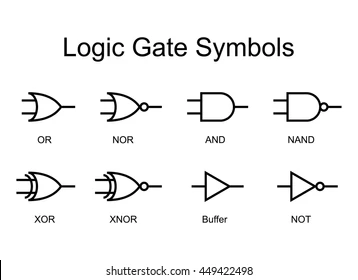
Logic Gate Symbols

Thoughts

프로그래밍을 배울 때 항상 코딩을 가능케 하는 컴퓨터의 근본 원리가 궁금했는데 pbs cs 를 들으면서 그 갈증이 너무나도 시원하게 해소되는 느낌이다. Abstract 계층을 작동시키는 physical 계층에 대해 배웠다. 바닥부터 하나하나 연결되는 느낌이다.