[day-18] 선형회귀

Joohyung Park·2024년 1월 23일

[모두연] 오름캠프

목록 보기

19/95

타겟이 연속형인 경우에 회귀를 적용한다

선형 회귀는 가장 기본적인 모델로 현실적으로는 잘 사용하지 않는다. 그렇지만 금융권이나 고객에게 무언가 설명하는 모델에 한해 회귀(로지스틱)모델을 사용한다고 한다. 이번에는 캘리포니아 집값 분석을 해보았다.

데이터 불러오기

import pandas as pd
dataset = pd.read_csv('/content/california_housing_train.csv')

데이터 분석

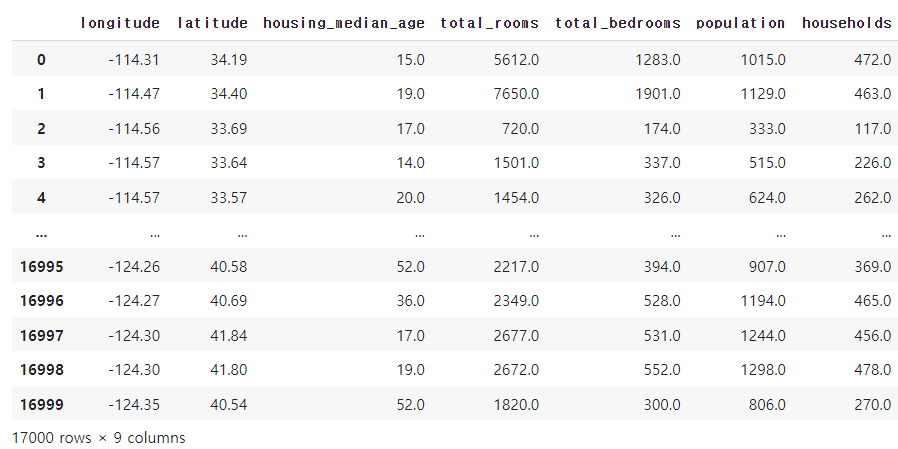
오른쪽을 가독성 때문에 조금 잘랐는데 총 17000개의 행과 9개의 칼럼이 존재한다. info를 찍어보면 결측치가 없는 것을 확인할 수 있다.

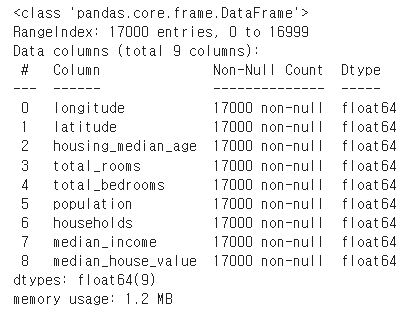
데이터 시각화 및 로그 변환

선형 모델에서는 변수들의 정규성이 중요하기에 비선형 관계나 극단값을 갖는 데이터에 로그 변환을 하여 분포를 안정화시킬 수 있다고 한다.

분포의 대칭성 개선
이상치 감소
비선형 관계 선형화

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

# 로그 변환 수행
df['log_median_income'] = np.log(df['median_income'])

# 원래 데이터와 로그 변환된 데이터의 분포 비교를 위한 시각화
plt.figure(figsize=(12, 6))

# 원래 데이터의 분포 (median_income)
plt.subplot(1, 2, 1)
sns.histplot(df['median_income'], kde=True, bins=30)
plt.title('Original Median Income Distribution')

# 로그 변환된 데이터의 분포 (log_median_income)
plt.subplot(1, 2, 2)
sns.histplot(df['log_median_income'], kde=True, bins=30)
plt.title('Log Transformed Median Income Distribution')

plt.tight_layout()
plt.show()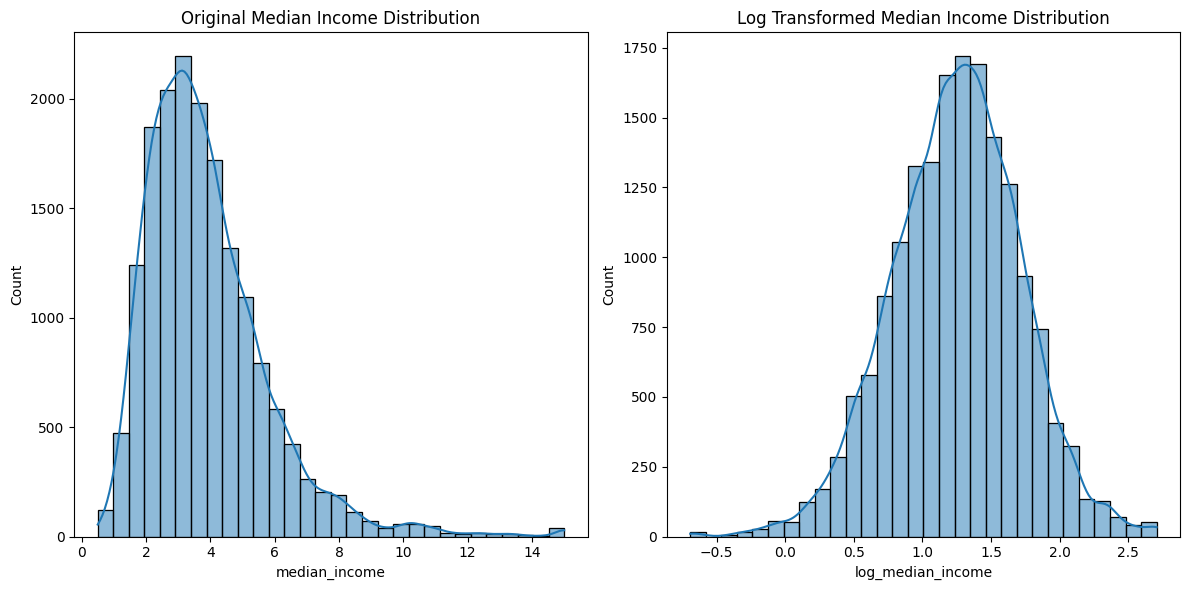

좀더 가운데로 온 모습(정규분포 형태)을 볼 수 있다. 로그변환된 데이터를 찍어보면 다음과 같다.

# 로그 변환된 데이터 확인
df[['median_income', 'log_median_income']].head()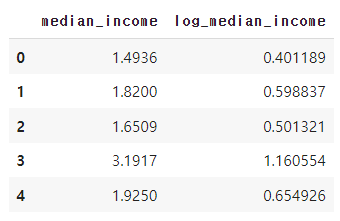

히스토그램과 상관 관계

강한 상관 관계를 가진 변수들은 문제를 일으킬 수 있고, 이는 특히 선형 회귀 모델에서 중요하다고 한다.

# 데이터 분포 확인을 위한 히스토그램
df.hist(bins=20, figsize=(12, 8))
plt.tight_layout()
plt.show()

# 상관 관계 분석을 위한 히트맵
plt.figure(figsize=(10, 8))
sns.heatmap(df.corr(), annot=True, fmt='.2f', cmap='coolwarm')
plt.show()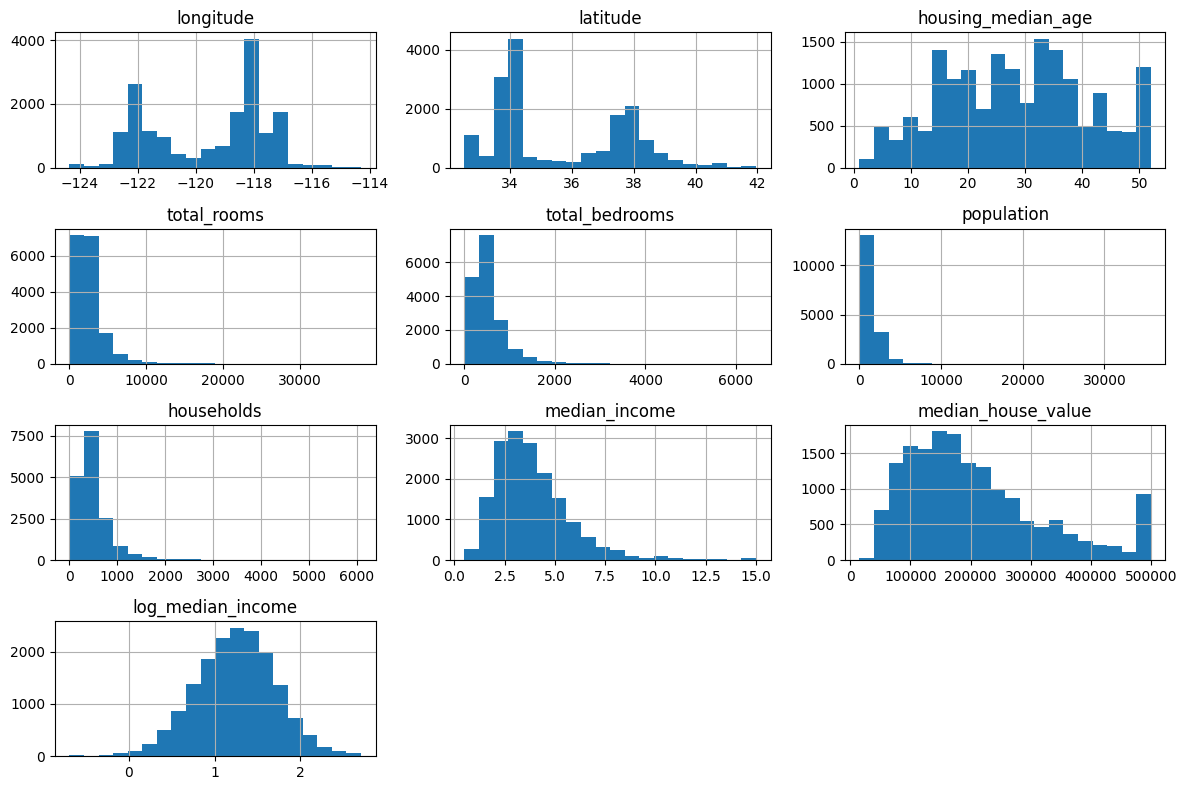

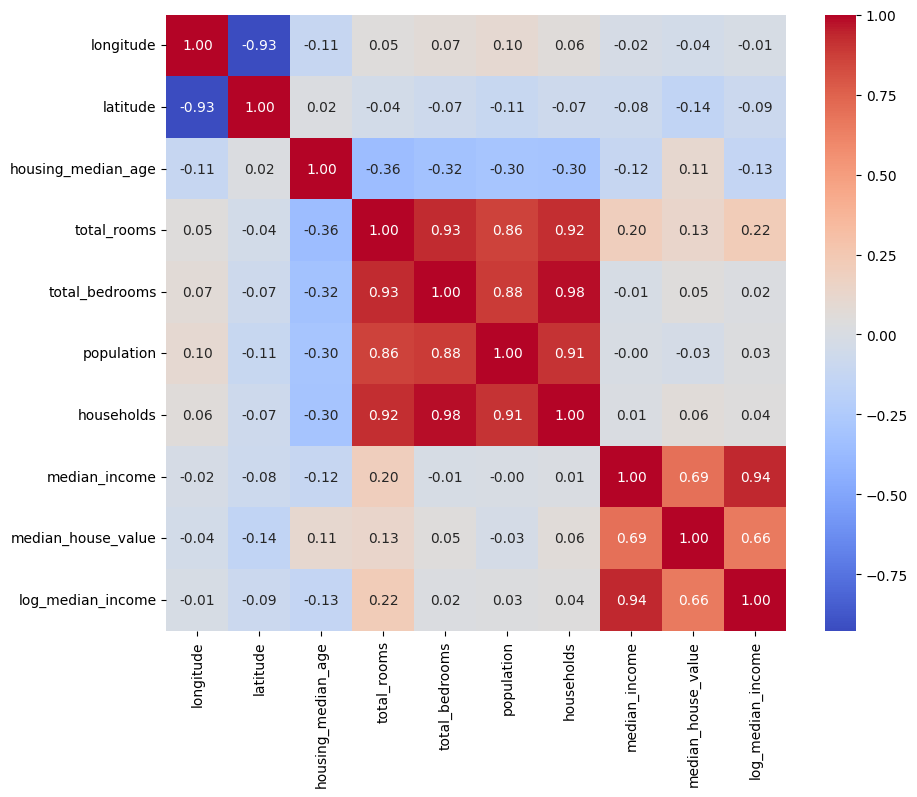
학습

from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score

# 독립변수와 종속변수 분리
X = df.drop('median_house_value', axis=1)
y = df['median_house_value']

# 학습 데이터와 테스트 데이터 분리
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=0)

# 선형 회귀 모델 생성 및 학습
model = LinearRegression()
model.fit(X_train, y_train)

사이킷런이라는 라이브러리를 통해 쉽게 학습 가능하다.

예측 및 평가

# 테스트 데이터에 대한 예측 수행
y_pred = model.predict(X_test)

# 모델 성능 평가
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print('MSE:', mse)
print('R² Score:', r2)

MSE, RMSE, R^2등의 평가 지표로 평가 가능하다.

계수 출력

# 선형 회귀 모델의 계수 출력
coefficients = pd.DataFrame(model.coef_, X.columns, columns=['Coefficient'])
print(coefficients)

# 계수의 중요도 해석
# 예: 'median_income'의 계수가 높고 유의미하다면, 
# 이 변수는 주택 가격에 큰 영향을 미치는 것으로 해석할 수 있다.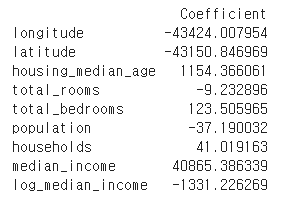

스케일링

from sklearn.preprocessing import StandardScaler

# 표준화를 위한 객체 생성
scaler = StandardScaler()

# 독립변수에 대한 스케일링 수행
X_scaled = scaler.fit_transform(X)

# 스케일링된 데이터로 학습 데이터와 테스트 데이터 분리
X_train_scaled, X_test_scaled, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=0)

# 스케일링된 데이터로 선형 회귀 모델 재학습
model_scaled = LinearRegression()
model_scaled.fit(X_train_scaled, y_train)

# 스케일링 전후 모델 성능 비교
y_pred = model.predict(X_test)
y_pred_scaled = model_scaled.predict(X_test_scaled)

mse_before = mean_squared_error(y_test, y_pred)
mse_after = mean_squared_error(y_test, y_pred_scaled)

print('MSE before scaling:', mse_before)
print('MSE after scaling:', mse_after)