[day-58] DFS, BFS, 정렬

저번 글에 이어서 트리 구조로 DFS, BFS를 구현해보도록 하겠습니다.

DFS, BFS

• 트리

class Node:
    def __init__(self, data):
        self.data = data
        # self.child = [] 2진 트리가 아닌 경우 child를 사용할 수 있습니다.
        self.left = None
        self.right = None

class Tree:
    def __init__(self, data):
        init = Node(data)
        self.root = init
        self.count = 0

    def __len__(self):
        return self.count

    def insert(self, data):
        new_node = Node(data)
        current_node = self.root

        while current_node:
            if data == current_node.data:
                return
            elif data < current_node.data:
                if not current_node.left:
                    current_node.left = new_node
                    self.count += 1
                    return
                current_node = current_node.left
            elif data > current_node.data:
                if not current_node.right:
                    current_node.right = new_node
                    self.count += 1
                    return
                current_node = current_node.right

• DFS(깊이 우선 탐색, 스택)
  

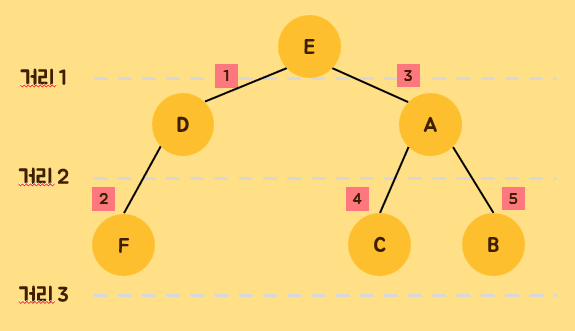
그림에서 알 수 있듯이, 한 방향으로 가면서 막힐 때까지 검사한다. 막히면 포기하고 마지막에 따라온 간선으로 되돌아 간다. 왼쪽부터 시작할 수도 있고, 오른쪽부터 시작할 수도 있다.

모든 노드를 방문하고자 하는 경우에 선택하는 알고리즘이다.

    def DFS(self):
        # 깊이우선탐색, DFS(Depth First Search)
        # Stack 이용!
        result = []
        stack = [self.root]

        while stack:
            current = stack.pop()
            if current.left:
                stack.append(current.left)
            if current.right:
                stack.append(current.right)
            result.append(current.data)

        return result

• BFS(넓이 우선 탐색, 큐)

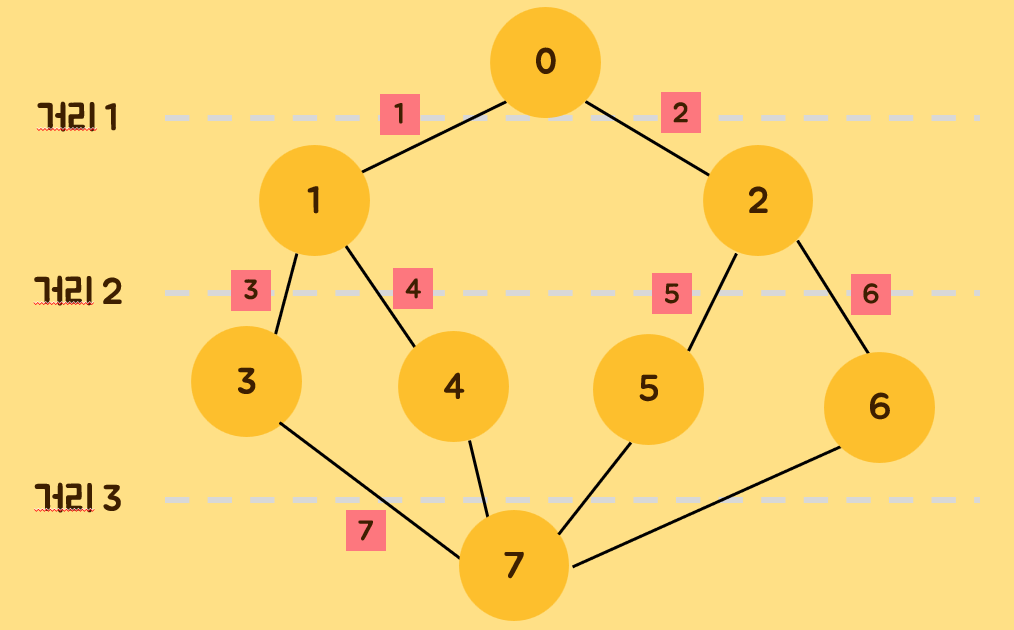
가까운 정점을 먼저 방문하고, 먼 정점은 나중에 방문하는 알고리즘이다. 마찬가지로 오른쪽부터 시작하거나 왼쪽부터 시작할 수 있다.

# 깊스너큐(깊이 우선 탐색은 스택, 너비 우선 탐색은 큐)
    def BFS(self):
        # 너비우선탐색, BFS(Breadth First Search)
        # Queue 이용
        result = []
        queue = [self.root]

        while queue:
            current = queue.pop(0)
            if current.right:
                queue.append(current.right)
            if current.left:
                queue.append(current.left)
            result.append(current.data)

        return result

BFS는 현재 노드를 맨 앞에서 꺼내고, DFS는 맨 뒤에서 꺼내는 것이 차이점이다.

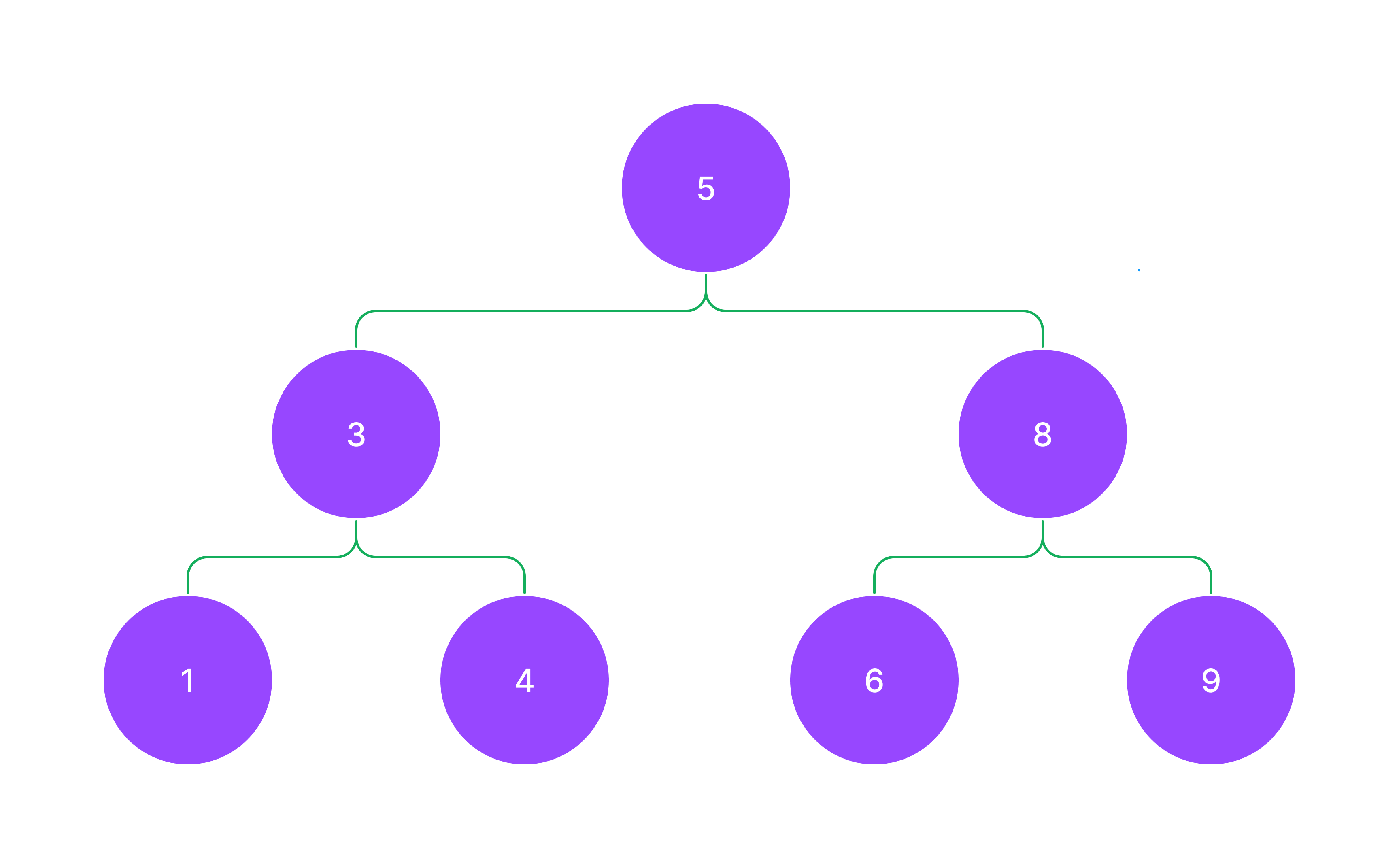
tree = Tree(5)
tree.insert(3)
tree.insert(8)
tree.insert(1)
tree.insert(4)
tree.insert(6)
tree.insert(9)

tree.BFS() # [5, 8, 3, 9, 6, 4, 1]
tree.DFS() # [5, 8, 9, 6, 3, 4, 1]

스택에는 나중에 방문할 노드를 먼저 넣기에 왼쪽 먼저 넣었으니 오른쪽부터 탐색하는 그림이 그려진다.

큐는 오른쪽부터 넣으면 그대로 오른쪽부터 탐색한다.

정렬

여러 정렬이 있지만 현재는 Timsort로 굳어지고 있다.
예전보다 중요도는 떨어졌지만 알아두면 쓰인다고 한다.

선택정렬

1. 먼저 전체 배열에서 최소값을 찾는다.
2. 최소값을 배열의 첫 번째 위치와 교환한다.
3. 두 번째 위치부터 나머지 배열에서 최소값을 찾아 두 번째 위치와 교환한다.
4. 과정 반복

def 최솟값_인덱스_리턴_함수 (리스트):
    최솟값인덱스 = 0
    for 증가값 in range(0, len(리스트)):
        if 리스트[증가값] < 리스트[최솟값인덱스]:
            최솟값인덱스 = 증가값
    return 최솟값인덱스

def 선택정렬(리스트):
    최종결과값 = []
    while 리스트:
        최솟값_인덱스_저장 = 최솟값_인덱스_리턴_함수(리스트)
        최솟값 = 리스트.pop(최솟값_인덱스_저장)
        최종결과값.append(최솟값)
    return 최종결과값

주어진리스트 = [199, 22, 33, 12, 32, 64, 72, 222, 233]

print(선택정렬(주어진리스트)) # [12, 22, 32, 33, 64, 72, 199, 222, 233]

삽입정렬

1. 배열의 두 번째 위치부터 시작한다.
2. 해당 위치의 요소를 이미 정렬된 부분과 비교하여 적절한 위치를 찾는다.
3. 해당 위치에 요소를 삽입하기 위해 그 앞까지의 요소들을 한 칸씩 뒤로 이동시킨다. (끼어들기 느낌)
4. 다음 위치로 이동하여 2-3 과정을 반복한다.

전 = [199, 22, 33, 12, 32, 64, 72, 222, 233]
후 = []

전 = [22, 33, 12, 32, 64, 72, 222, 233]
후 = [199]

전 = [33, 12, 32, 64, 72, 222, 233]
후 = [22, 199]

전 = [12, 32, 64, 72, 222, 233]
후 = [22, 33, 199]

전 = [32, 64, 72, 222, 233]
후 = [12, 22, 33, 199]

전 = [64, 72, 222, 233]
후 = [12, 22, 32, 33, 199]

전 = [72, 222, 233]
후 = [12, 22, 32, 33, 64, 199]

def 삽입값이들어갈_인덱스 (결과값, 삽입값):
    for 증가값 in range(0, len(결과값)):
        if 삽입값 < 결과값[증가값]:
            return 증가값
    return len(결과값)

def 삽입정렬(입력_리스트_하나):
    결과값 = []
    while 입력_리스트_하나:
        삽입값 = 입력_리스트_하나.pop(0)
        삽입값_인덱스 = 삽입값이들어갈_인덱스(결과값, 삽입값)
        결과값.insert(삽입값_인덱스, 삽입값)
    return 결과값

주어진리스트 = [199, 22, 33, 12, 32, 64, 72, 222, 233]

print(삽입정렬(주어진리스트))

병합정렬(분할 정복)

1. 분할 : 입력 배열을 같은 크기의 두 개의 배열로 자른다. 재귀적으로 진행되며, 하나의 배열 원소만 남을때까지 진행한다.
2. 정복 : 분할된 작은 배열들을 정렬한다. 길이가 1인 배열은 정렬된 상태이다.
3. 병합 : 두 개의 정렬된 배열을 하나의 정렬된 배열로 합친다. 두 배열에서 값을 비교하여 작은 값부터 새로운 배열에 담는다.

입력값 = [5, 10, 66, 77, 54, 32, 11, 15]
정렬된배열 = []

# 분할(이해를 돕기 위해 8개로 조정)
[5, 10, 66, 77, 54, 32, 11, 15]
[5, 10, 66, 77], [54, 32, 11, 15]
[5, 10], [66, 77], [54, 32], [11, 15]
[5], [10], [66], [77], [54], [32], [11], [15]

# 정복(0번째끼리 비교!)
[5, 10], [66, 77], [32, 54], [11, 15]
[5, 10], [66, 77], [32, 54], [11, 15]
[5, 10, 66, 77], [11, 15, 32, 54]
[5, 10, 11, 15, 32, 54, 66, 77]

def 병합정렬(입력리스트):
    # print(입력리스트)
    입력리스트길이 = len(입력리스트)
    if 입력리스트길이 <= 1:
        return 입력리스트
    중간값 = 입력리스트길이 // 2
    그룹_하나 = 병합정렬(입력리스트[:중간값])
    그룹_둘 = 병합정렬(입력리스트[중간값:])

    결과값 = []

    while 그룹_하나 and 그룹_둘:
        if 그룹_하나[0] < 그룹_둘[0]:
            결과값.append(그룹_하나.pop(0))
        else:
            결과값.append(그룹_둘.pop(0))
    if 그룹_하나:
        결과값.extend(그룹_하나)
        그룹_하나.clear()
    if 그룹_둘:
        결과값.extend(그룹_둘)
        그룹_둘.clear()
    return 결과값

주어진리스트 = [199, 22, 33, 12, 32, 64, 72, 222, 233]

print(병합정렬(주어진리스트))

페이지 교체 알고리즘

FIFO 알고리즘

오래된 원소가 가장 빨리 나간다.

# 순서 : 0, 4, 6, 5, 4, 7, 8
[]
[0]
[0, 4]
[0, 4, 6]
[4, 6, 5]
[4, 6, 5] # 4가 hit
[6, 5, 7]
[5, 7, 8]

LRU 알고리즘

오랫동안 사용되지 않은 원소가 삭제된다.

# 순서 : 0, 4, 6, 5, 4, 7, 8
[]
[0]
[0, 4]
[0, 4, 6]
[4, 6, 5]
[6, 5, 4] # 4가 hit
[5, 4, 7]
[4, 7, 8]

실행 시간을 구하는 문제에 주로 사용된다.

예시

• hit - 1초
• miss - 5초
• 캐시(큐 길이) - 3

["바나나", "체리", "한라봉", "자몽", "수박", "수박", "체리"]
[바나나] # 5
[바나나, 체리] # 5
[바나나, 체리, 한라봉] # 5
[체리, 한라봉, 자몽] # 5
[한라봉, 자몽, 수박] # 5
[한라봉, 자몽, 수박] # 1 - hit
[자몽, 수박, 체리] # 5

큐의 길이가 제한되어 있으며 최대 길이를 넘으면 일반적으로 오래된 원소가 삭제된다.

만약, 현재 큐에 있는 원소가 추가된다고 하면 해당 원소는 꺼내진 후 맨 뒤에 append 된다. 이 과정을 hit 이라고 한다. 위 예제에서는 1초이다.

슬라이딩 윈도우, 투 포인트

슬라이딩 윈도우

연속된 2개의 합이 10인 모든 수를 찾는 것과 같은 문제의 알고리즘이다. 구간의 넓이는 고정되어 있다.

def find_pairs_sum(nums, target_sum):
    result = []
    window_sum = nums[0] + nums[1]
    left = 0
    right = 1

    while right < len(nums):
        if window_sum == target_sum:
            result.append((nums[left], nums[right]))
            window_sum -= nums[left]
            left += 1
            window_sum += nums[right + 1]
            right += 1
        elif window_sum < target_sum:
            right += 1
            if right < len(nums):
                window_sum += nums[right]
        else:
            window_sum -= nums[left]
            left += 1

    return result

nums = [1, 5, 4, 6, 4, 6, 7, 6, 4, 3, 1, 2]
target_sum = 10
print(find_pairs_sum(nums, target_sum))

투 포인트

연속된 배열의 합이 10인 배열의 인덱스를 모두 찾아라..와 같은 문제이다. 구간의 넓이가 조건에 따라 유동적으로 변하는 알고리즘이다.

def solution(data, require_value):
    start_pointer = 0
    end_pointer = 0
    temp_sum = 0

    data_len = len(data)
    result = []

    for start_pointer in range(data_len):
        while temp_sum < require_value and end_pointer < data_len:
            temp_sum += data[end_pointer]
            end_pointer += 1
        if temp_sum == require_value:
            result.append([start_pointer, end_pointer-1])
        temp_sum -= data[start_pointer]
    return result

solution([1, 5, 4, 6, 4, 6, 7, 6, 4, 3, 1, 2], 10) 
# [[0, 2], [2, 3], [3, 4], [4, 5], [7, 8], [8, 11]]

1. 현재까지의 합이 목표보다 작고 엔드 포인터가 리스트의 끝값이 아니라면, 엔드 포인터 인덱스의 값을 더하고 엔드포인터를 한칸 증가시킨다.
2. 만약 현재까지의 합이 목표와 같다면, 결과 배열에 현재 쌍을 추가한다.
3. 다음 부분의 합을 계산하기 위해 이전 부분 배열에 포함시켰던 값을 빼준다. 중복 계산 방지를 위함이다.

참고

위니브 이호준 강사님의 ppt자료를 받아 작성하였습니다.