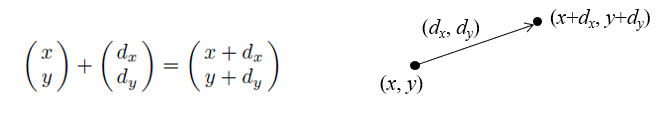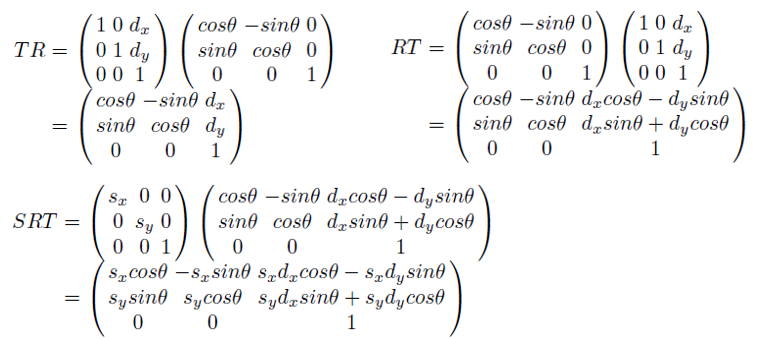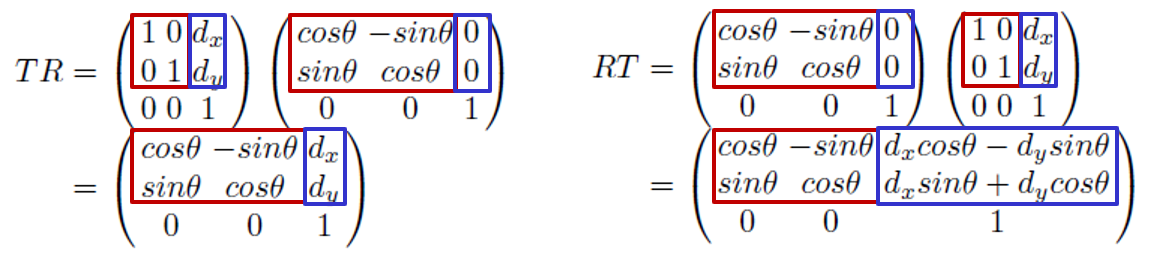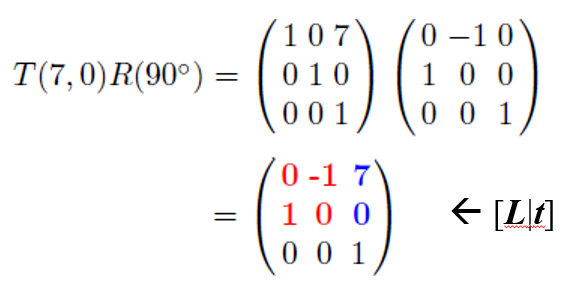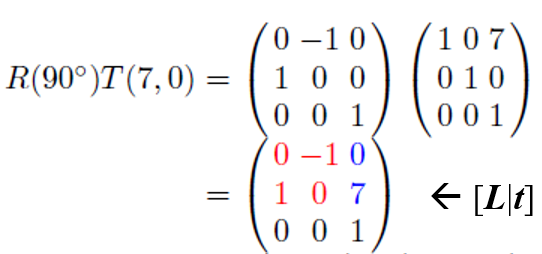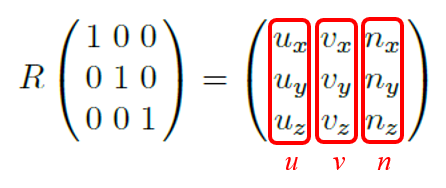[CG/개념] Introduction to Computer Graphics with OpenGL ES CH04: Spaces and Transforms

Jinn Aha·2025년 1월 21일

Intro to Computer Graphics

목록 보기

2/2

이 시리즈에서는 고려대학교 한정현 교수님의 Computer Graphics 강의에서 공부한 내용을 정리해보고자 한다. 강의는 교수님의 저서 Introduction to Computer Graphics with OpenGL ES 를 바탕으로 진행되었다.

CH04: Spaces and Transforms

Key Points

2D, 3D 공간의 오브젝트의 Scaling, Rotation, Translation

세 Transform의 composition과 Affine Transform

World Space - Object Space의 관계와 표현

Rotation, Scaling and Translation

Rotation(회전), Scaling(확대/축소), Translation(이동) 은 그래픽스에서 객체의 Transform(변환) 을 표현하기 위해 사용된다.

선형 변환인 Rotation, Scaling과 Translation은 행렬을 통해 나타낼 수 있다. 이 때 삼차원 공간의 정점 $(x,y,z)$ 의 Rotation, Scaling은 3X3 행렬로, Translation은 4X4 행렬로 나타낸다.

Scaling

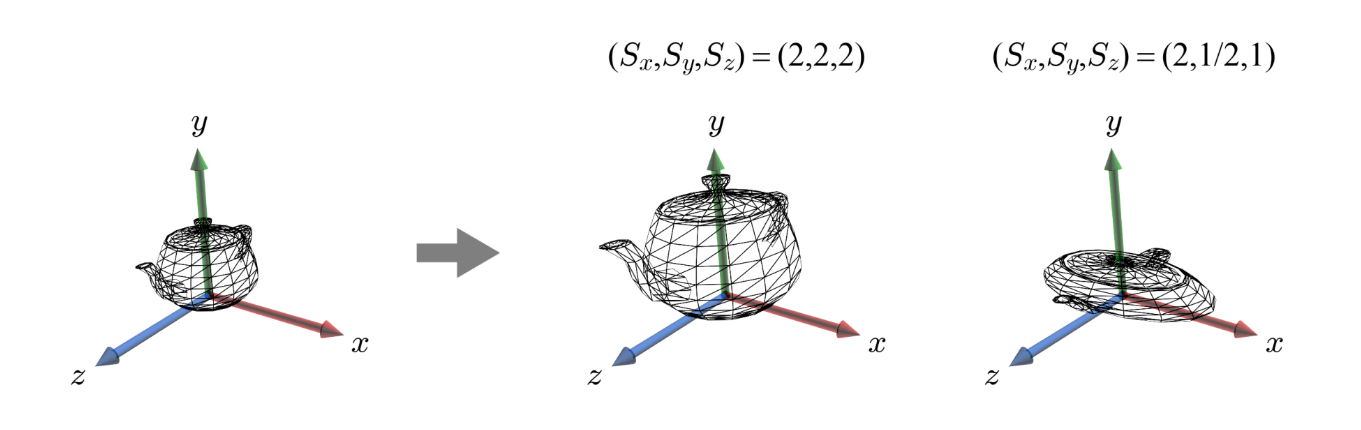
물체의 Scaling은 다음과 같이 정사각 대각 행렬로 나타낸다:

S= \left(\begin{array}{ccc} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{l} s_x x \\ s_y y \\ s_z z \end{array}\right)

그림과 같이 특정 방향만으로도 확대/축소가 가능하다.

Rotation

Rotation은 $(x,y,z)$ 처럼 직교좌표계로 표현된 좌표를 극좌표계로 변환하는 과정을 안다면 쉽게 표현할 수 있다.

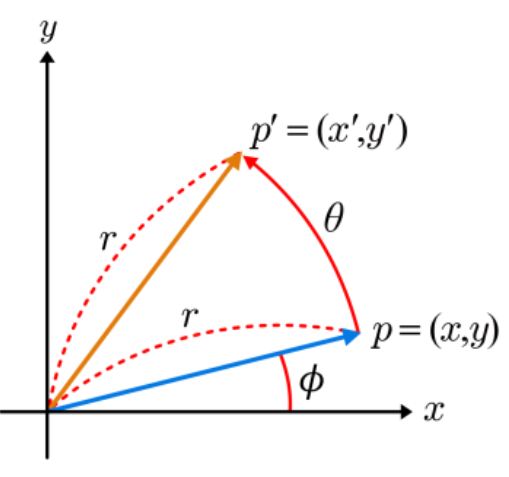
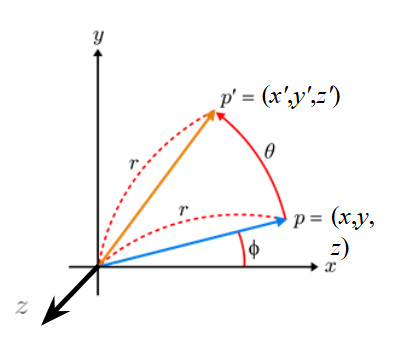
먼저 2차원 공간에서 벡터 $(x,y)$ 를 원점을 기준으로 $\theta$ 만큼 회전시킨 $(x',y')$ 를 구하는 과정에서 회전행렬 $R$ 을 유도할 수 있다. 그 과정은 다음과 같다:

\begin{aligned} x& =r \cos \phi \\ y& =r \sin \phi \\\\ x^{\prime}& =r \cos (\phi+\theta) \\ & =r \cos \phi \cos \theta-r \sin \phi \sin \theta \\ & =x \cos \theta-y \sin \theta \\ y^{\prime}& =r \sin (\phi+\theta) \\ & =r \cos \phi \sin \theta+r \sin \phi \cos \theta \\ & =x \sin \theta+y \cos \theta \end{aligned}

결과적으로 Rotation은 2차원에서 다음과 같이 나타낸다:

R=\left(\begin{array}{cc} \cos \theta &-\sin \theta \\ \sin \theta & \cos \theta \end{array}\right)

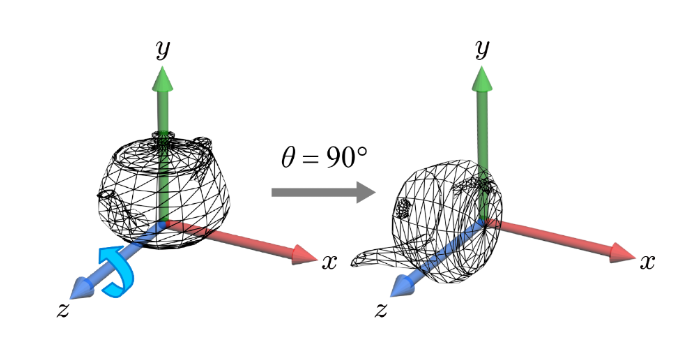
3차원으로 확장될 때는 어떨까? 점을 중심으로 회전이 이뤄지는 2차원과 달리 3차원에서는 축을 중심으로 회전이 일어난다.

그러나 생각해보면, 한 축 $z$ 를 기준으로 회전이 발생할 때, 각 정점의 회전 후의 $z$ 좌표 $z'$ 은 변하지 않는다. 이는 회전축이 되는 방향에서는 좌표 변화가 없고, 다른 두 방향에서만 좌표의 변화가 일어난다는 것을 의미한다.

각 회전축을 중심으로 하는 회전을 각각 $R_x, R_y, Rz$ 라 하자. 하나의 회전에 대한 표현을 구하면, 나머지 두 회전은 각 회전이 반시계 방향(CCW)으로 이루어진다는 점과 축의 상대적인 위치 변화를 바탕으로 유도할 수 있다.

구체적으로, $z$ 축을 기준으로 90° 회전이 이루어질 경우, $x$ 축은 $y$ 축의 위치로 회전한다. 이와 같은 방식으로, $x$ 축을 기준으로 90° 회전할 경우 $y$ 축이 $z$ 축 위치로 이동한다. 마찬가지로, $y$ 축을 기준으로 90° 회전하면 $z$ 축이 $x$ 축 위치로 회전한다. 이러한 관계를 이용하면 $R_x$ , $R_y$ , $R_z$ 회전 행렬을 모두 유도할 수 있다.

이렇게 구해진 $R_x, R_y, Rz$ 는 다음과 같다:

R_x=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \theta & -\sin \theta\\ 0 & \sin \theta & \cos \theta \end{array}\right)\ R_y=\left(\begin{array}{ccc} \cos \theta & 0 & \sin \theta\\ 0 & 1 & 0 \\ -\sin \theta & 0 & \cos \theta \end{array}\right)\ R_z=\left(\begin{array}{ccc} \cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{array}\right)

Translation & Homogeneous Coordinates

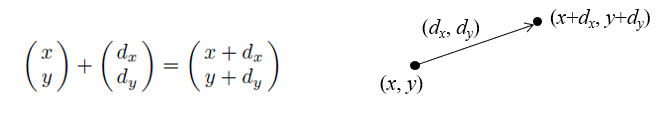
Translation은 물체의 이동을 나타내고, vector addition으로 간단히 표현된다. 그러나 그래픽스에서 물체는 세 가지 transform 중 한가지 변환만을 거치지 않는다. 따라서 transform을 rotation, scaling과의 일관성을 유지하기 위해 matrix multiplication으로 표현해야 한다. 이를 위해서 homogeneous coordinates가 요구된다.

Homogeneous Coordinates

Homogeneous Coordinates(동차 좌표계)는 $N$ 차원의 벡터 혹은 정점을 표현할 때 $N+1$ 차원의 표현을 사용하는 방식으로, 컴퓨터그래픽스나 컴퓨터 비전에서 흔히 사용된다. 예를 들어, $(x,y)$ 를 표현할 때 $(x,y,1)$ 처럼 마지막 요소로 1을 추가해 줄 수 있다.

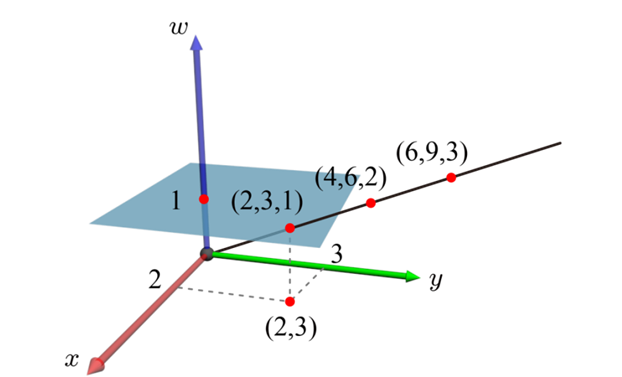
그러나 마지막 요소가 항상 1이어야 하는 것은 아니다. 1을 $w$ 로 바꾸어주면, 하나의 cartesian 좌표는 0과 이 좌표를 이어 $(wx, wy, w)$ 로 표현되는 직선과 $w=1$ 의 교점으로 볼 수 있다. 그리고 0이 아닌 weight $w$ 에 의해 하나의 cartesian 좌표로 무한하게 많은 동차 좌표계의 정점을 만들 수 있다.

Homogeneous Coodinates를 이용하면 vector addition으로 표현된 translation을 다음과 같이 matrix multiplication으로 표현할 수 있다:

2차원의 경우
$T=\left(\begin{array}{cccc}1 & 0 & d_x \\ 0 & 1 & d_y \\ 0 & 0 & 1 \end{array}\right)\left(\begin{array}{c}x \\ y \\ 1\end{array}\right)=\left(\begin{array}{c}x+d_x \\ y+d_y \\ 1\end{array}\right)$
3차원의 경우
$T=\left(\begin{array}{cccc}1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1\end{array}\right)\left(\begin{array}{c}x \\ y \\ z \\ 1\end{array}\right)=\left(\begin{array}{c}x+d_x \\ y+d_y \\ z+d_z \\ 1\end{array}\right)$

이제 $S$ , $R$ 행렬도 마찬가지로 일관성있게 표현해주면 translation, scaling, rotation은 최종적으로 다음과 같이 표현된다:

T=\left(\begin{array}{cccc}1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1\end{array}\right)\ S= \left(\begin{array}{cccc} s_x & 0 & 0 & 0\\ 0 & s_y & 0 & 0\\ 0 & 0 & s_z & 0\\ 0 & 0 & 0 & 1 \end{array}\right)

R_x=\left(\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & \cos \theta & -\sin \theta & 0\\ 0 & \sin \theta & \cos \theta & 0\\ 0 & 0 & 0 & 1 \end{array}\right)\ R_y=\left(\begin{array}{cccc} \cos \theta & 0 & \sin \theta & 0\\ 0 & 1 & 0 & 0\\ -\sin \theta & 0 & \cos \theta & 0\\ 0 & 0 & 0 & 1 \end{array}\right)\ R_z=\left(\begin{array}{cccc} \cos \theta & -\sin \theta & 0 & 0\\ \sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right)

Transform Composition and Affine Transform

Affine Transform은 쉽게 말해 선형 변환 + Translation이다. Translation은 선형 변환이기 위한 조건인 1) closed under addition 2) closed under matrix multiplication 두 조건을 모두 만족하지 못한다. 따라서 하나의 transform으로 $S, R, T$ 를 모두 묶어주기 위해서는 Affine 공간에서의 연산이 필요해진다.

앞에서 언급된 Homogeneous Coordinate를 다시 생각해보자. 이를 사용하는 이유가 무엇일까? 우리가 다루는 transform이 벡터공간이 아닌 Affine 공간에서 일어나는 transform이기 때문이다.

벡터는 크기와 방향을 가지지만, 위치정보를 가지지 않는다. 그러나 '이동'을 표현하기 위해서는 우선 위치에 대한 정보가 필요하다. 이 때 위치를 표현하기 위한 '정점'이 포함된 공간인 Affine Space이며 이 공간에서의 transform이 Affine Transform으로 정의된다.

앞서 $S, R, T$ 행렬의 차원을 맞추어 준 이유는 세 transform 사이의 concat을 용이하게 만들어 연속적인 물체의 변환을 표현하기 위함이었다. 그러나 여전히 반복되는 transform의 계산은 쉬운 편이 아니다. 다음 이미지는 RT, TR, SRT의 concat 결과를 보여준다.

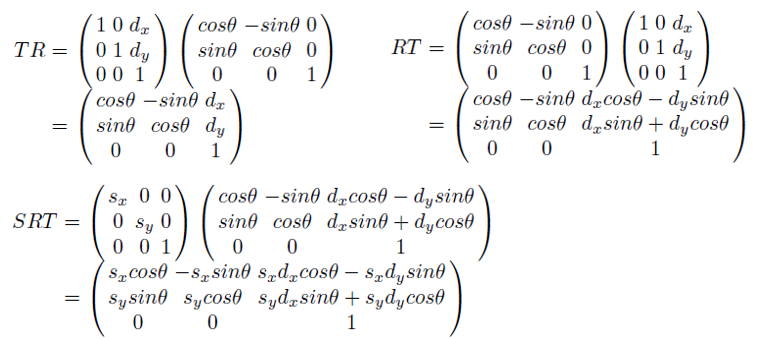
직관적으로 알 수 있는 것 두가지는, 첫째, 계산하기 귀찮아보인다는 것. 둘째, TR과 RT의 결과가 다르다는 것 (이것은 당연하게도, matrix multiplication에서 교환법칙이 성립하지 않기 때문이다). 두 번째 특징은 직관적으로 아래 이미지와 같이 먼저 회전하고 이동하는 것과 먼저 이동하고 회전하는 것이 다르다는 것으로 이해할 수도 있다.

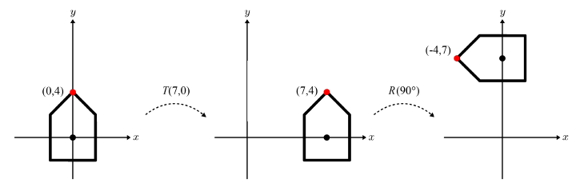
그리고 우리가 더 주의깊게 살펴보아야 할 두가지 특성은 다음과 같다:

얼마나 많은 transform이 concat 되던지 항상 마지막 행은 (0 0 $\cdots$ 0 1)로 끝난다. 따라서 이 행을 제외하고 계산을 간단하게 만들 수 있다.
마지막 열을 제외하면 앞 행들은 오로지 선형변환의 combination으로만 이루어져 있다. 즉, 입력되는 translation의 term을 포함하지 않는다.

이 두 특성을 활용해 Affine Transform 계산을 간소화할 수 있다. 계속해서 2차원의 경우로 생각해 보자. 항상 동일한 3행을 제외한 $2\times3$ 요소를 $[L|t]$ 로 표현할 수 있다.

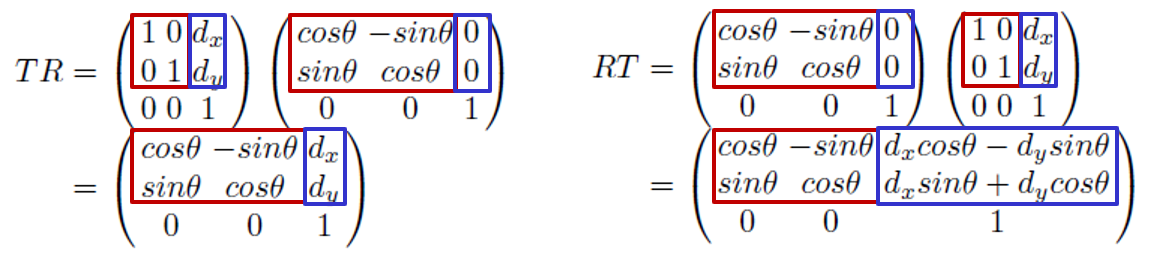
수식에서 빨갛게 표시한 부분이 $L$ , 파랗게 표시한 부분이 $t$ 로, 각각

$L$ : 선형변환으로만 이뤄진 $2\times2$ combined linear transfrom
$t$ : translation과 선형변환의 combination으로 이루어진 combined translation

이다.

이렇게 표현했을 때의 장점은, $L$ 과 $t$ 를 분리하여 transform의 concat 순서와 관계없이 "L 먼저, t 나중에" 계산하는 일관적인 규칙을 따를 수 있다는 것이다. 어짜피 $L$ 부분은 translation과 섞이지 않으므로 linear transform끼리 먼저 계산하고, $t$ 부분은 '선형변환된 객체의 이동'이라는 관점에서 계산해준다.

위의 이미지로 예를 들자면,

$RT$ : Rotation + rotation된 Translation
$TR$ : Rotation + Translation

으로 나누어 생각한다면 회전이 먼저이든 이동이 먼저이든 일관적 순서로 계산할 수 있다.
(7,0) 이동과 90° 회전이라는 구체적인 상황을 예로 들면 다음과 같다.

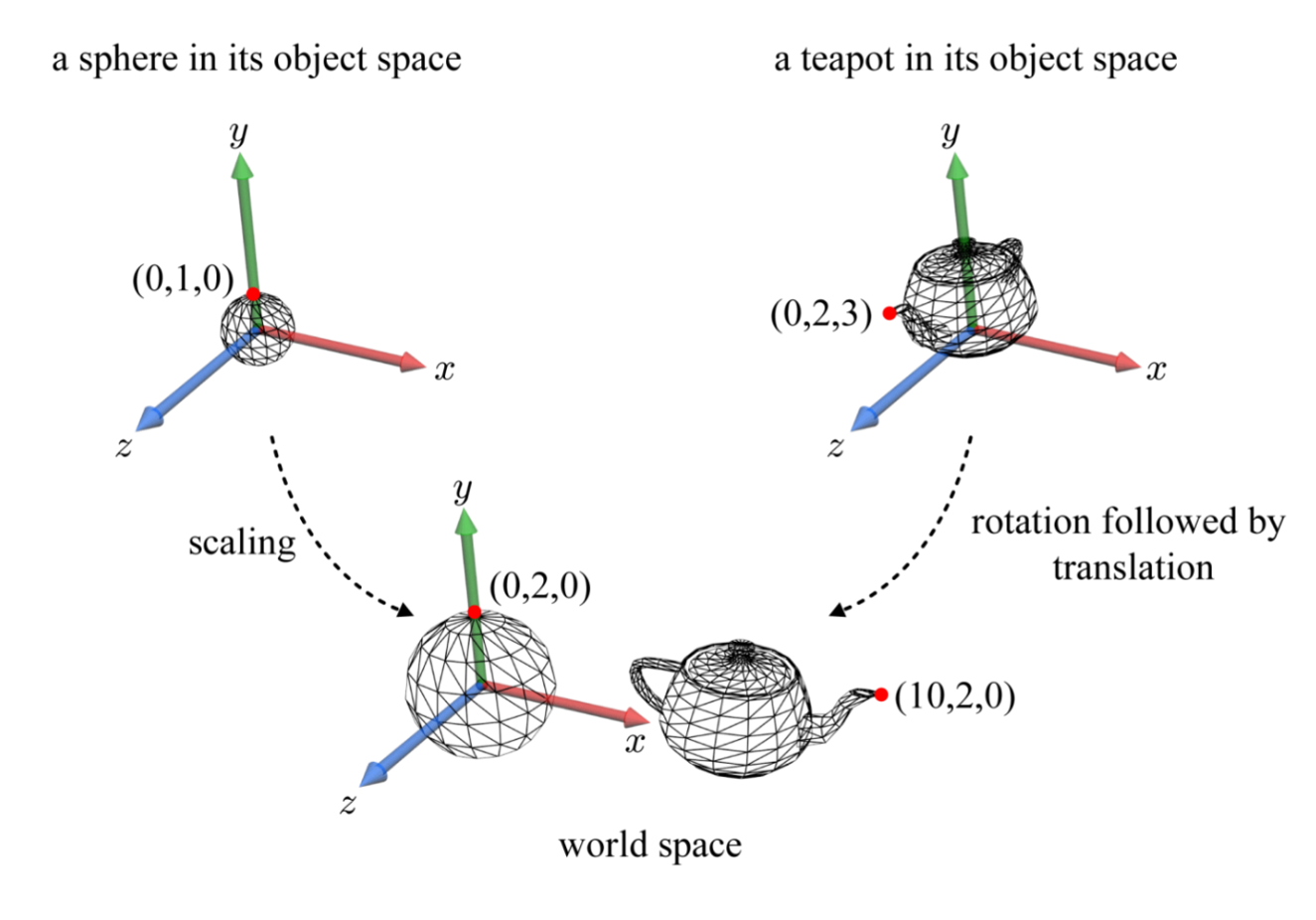
World Space and Object Space

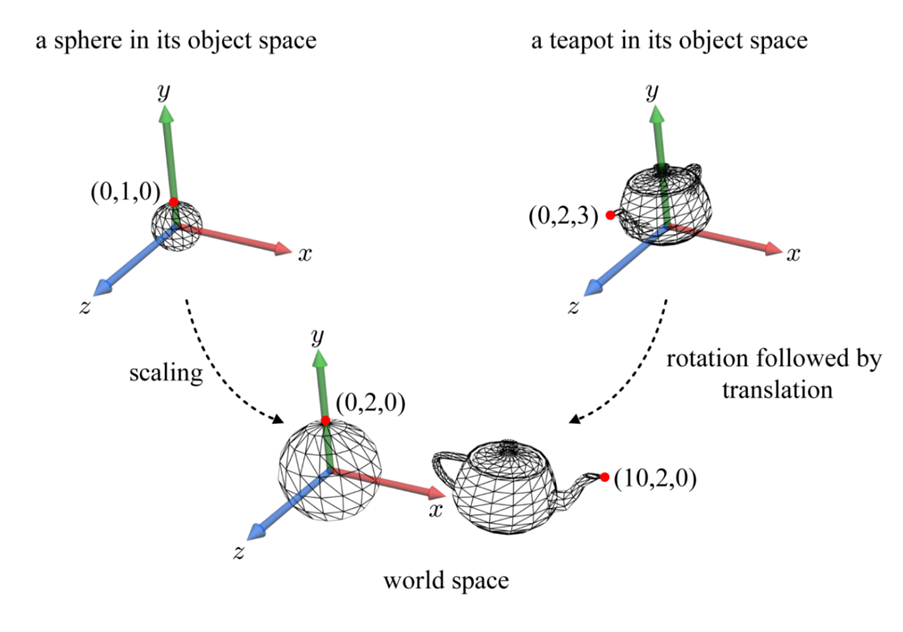
물체가 정의될 때 물체 각각에 대한 좌표계는 Object Space라고 불린다. Object Space와 물체의 관계는 서로 묶여있다고 생각하면 쉽다. 즉, 물체를 움직이는 것이 곧 Object Space를 움직이는 것이다. 그래픽스에서 삼차원 공간의 물체들은 각각의 독립적인 Object Space를 가진다. 그렇기 때문에 하나의 scene에 여러 물체를 위치시키고 변환시키기 위해서는 하나의 통일된 좌표계가 필요하다. 이것이 World Space이다. 물체들은 각자의 world transform을 거쳐 World Space라는 공간상에서 변형된다.

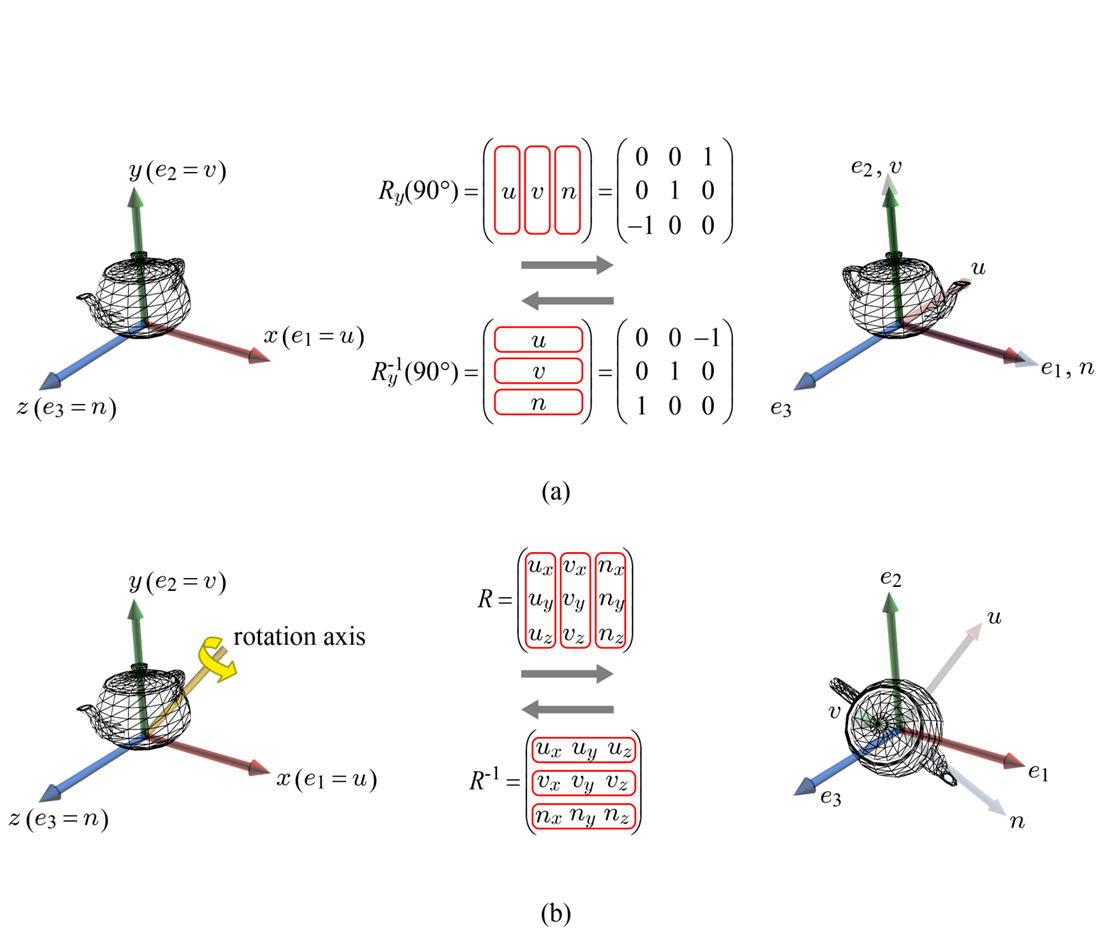
처음 물체가 생성될 때, object space는 world space와 동일한 기저를 가진다. Object Space의 기저를 ${u, v, n}$ 이라 하고, World Space의 기저를 ${e_1, e_2, e_3}$ 이라 할 때, 다음 그림처럼 물체를 회전시키면 World Space에 대해 Object Space의 기저는 회전한다.

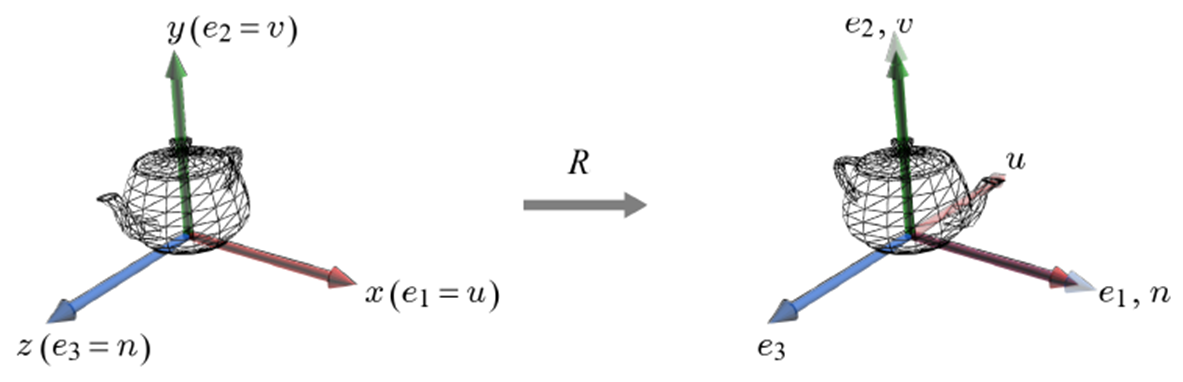
그렇다면 Object Space 기저를 회전시키는 회전 변환 $R$ 은 어떻게 찾을까? 재미있는 지점은, 결론적으로 $R = (\bold{u}\ \bold{v}\ \bold{n})$ 이라는 점이다. World Space의 기저를 표준기저 ${e_1, e_2, e_3}$ 로 설정했기 때문에,

R\left(\begin{array}{l} 1 \\ 0 \\ 0 \end{array}\right)=\left(\begin{array}{l} u_x \\ u_y \\ u_z \end{array}\right), \quad R\left(\begin{array}{l} 0 \\ 1 \\ 0 \end{array}\right)=\left(\begin{array}{c} v_x \\ v_y \\ v_z \end{array}\right), \quad R\left(\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right)=\left(\begin{array}{l} n_x \\ n_y \\ n_z \end{array}\right)

이고, 따라서

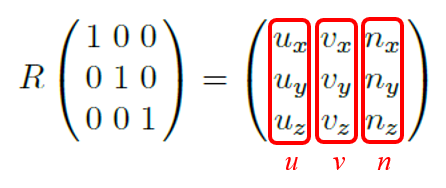
이 된다.

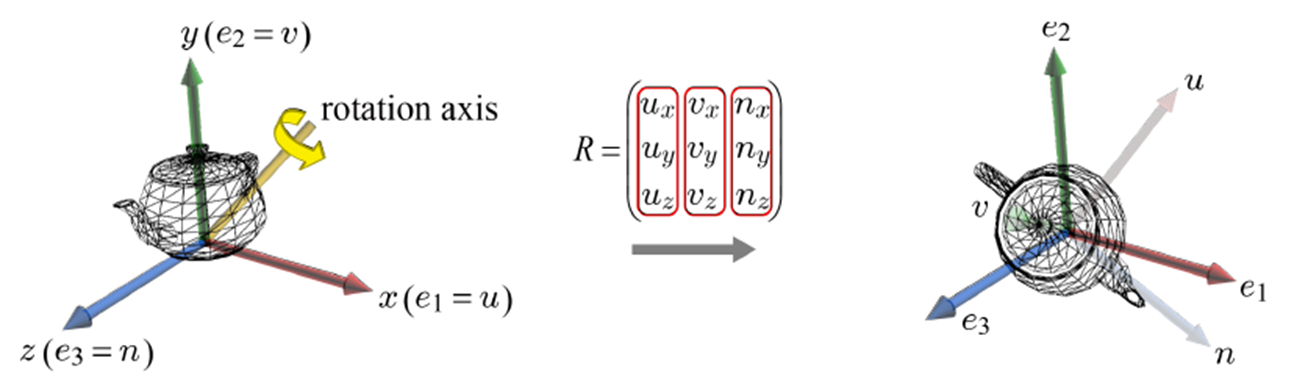
이는 회전 축이 기저와 일치하지 않는 상황에서도 동일하게 적용된다.

Inverse Transform

수행한 변환에 역행렬을 곱해주면 다시 원래 상태로 변환하는 것이 가능하다. 역행렬은 간단하게 다음과 같이 구한다.

Scaling

S^{-1}= \left(\begin{array}{cccc} \frac{1}{s_x} & 0 & 0 \\ 0 & \frac{1}{s_y} & 0 \\ 0 & 0 & \frac{1}{s_z} \end{array}\right) \Leftrightarrow\left(\begin{array}{cccc} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{array}\right)

Translation

Inverse translation $T^{-1}= \left(\begin{array}{llll} 1 & 0 & 0 & -d_x \\ 0 & 1 & 0 & -d_y \\ 0 & 0 & 1 & -d_z \\ 0 & 0 & 0 & 1 \end{array}\right) \Leftrightarrow\left(\begin{array}{llll} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{array}\right)$