
이진 검색
정의
오름차순 또는 내림차순으로 정리된 배열에서 검색 범위를 줄여나가며 검색 값을 찾는 알고리즘
오름차순으로 정렬된 배열의 중간값을 기준으로 하여, 찾고자 하는 값이 중간값보다 작으면 중간값의 왼쪽 배열을, 크면 중간값의 오른쪽 배열을 검색하고 이 방식을 끊임없이 진행하는 개념이다.
설명
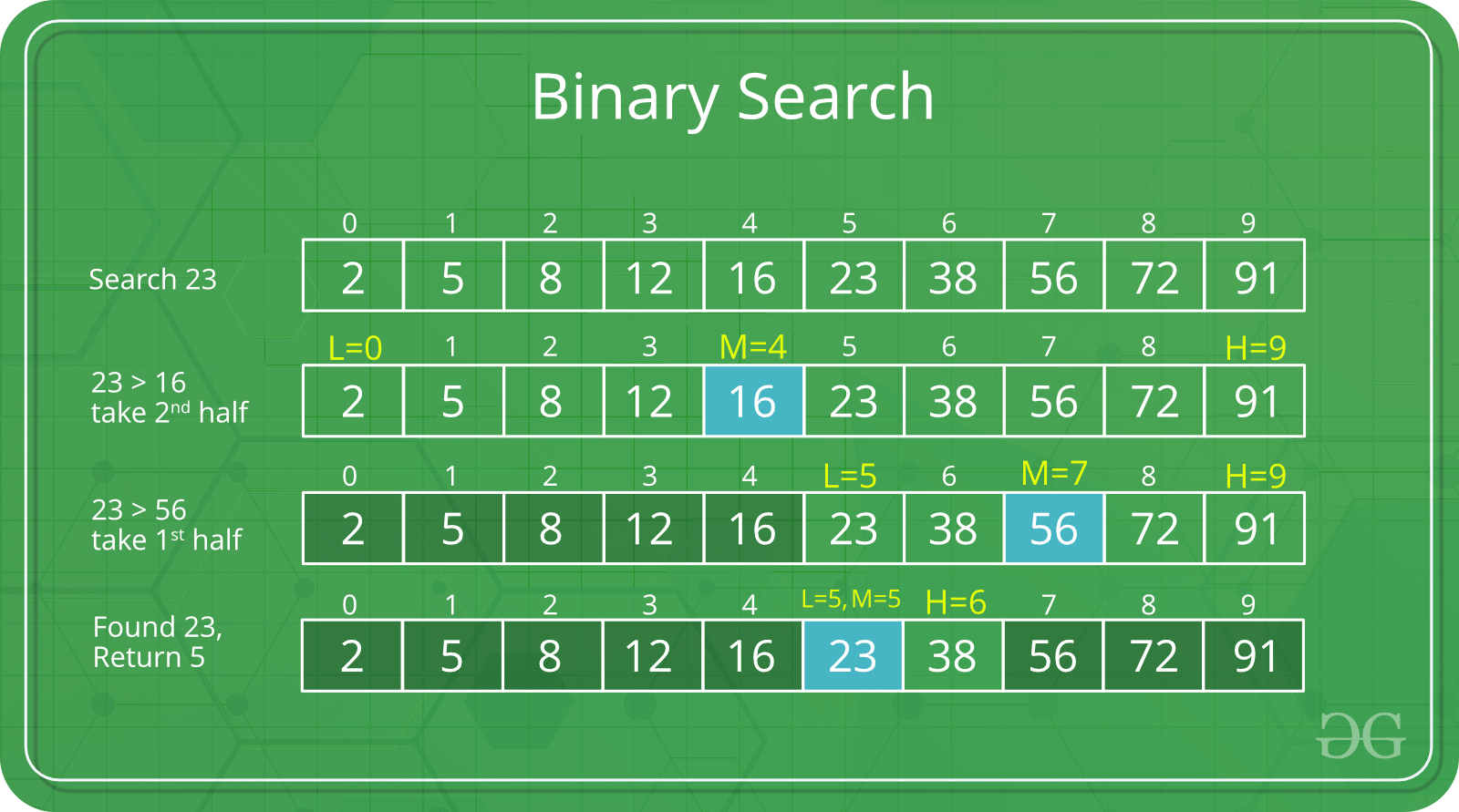
- 오름차순으로 정렬된 배열
[2, 5, 8, 12, 16, 23, 38, 56, 72, 91]에서23을 검색하고자 할 때
- 배열의 중간값(
(left+right)//2)을 기준으로 대소 비교
23은16보다 크므로 왼쪽 배열은 고려하지 않고 오른쪽 배열을 검색
- 해당 배열의 중간값
56을 기준으로 23과 대소 비교
23은56보다 작으므로 오른쪽 배열은 고려하지 않고 왼쪽 배열을 검색
- 최종적으로
23검색 완성
이진 검색 종료 조건
이진 검색이 종료되기 위해서는 아래 두가지 조건 중 하나가 충족되어야 한다는 것을 알 수 있다.
1. 중간값이 키값과 일치하는 경우 - 검색 성공
2. 검색 범위가 더이상 존재하지 않는 경우 (left > right일 때) - 검색 실패
코드
검색 종료 조건을 모두 반영한 이진 검색을 파이썬으로 구현해보자면 아래와 같다.
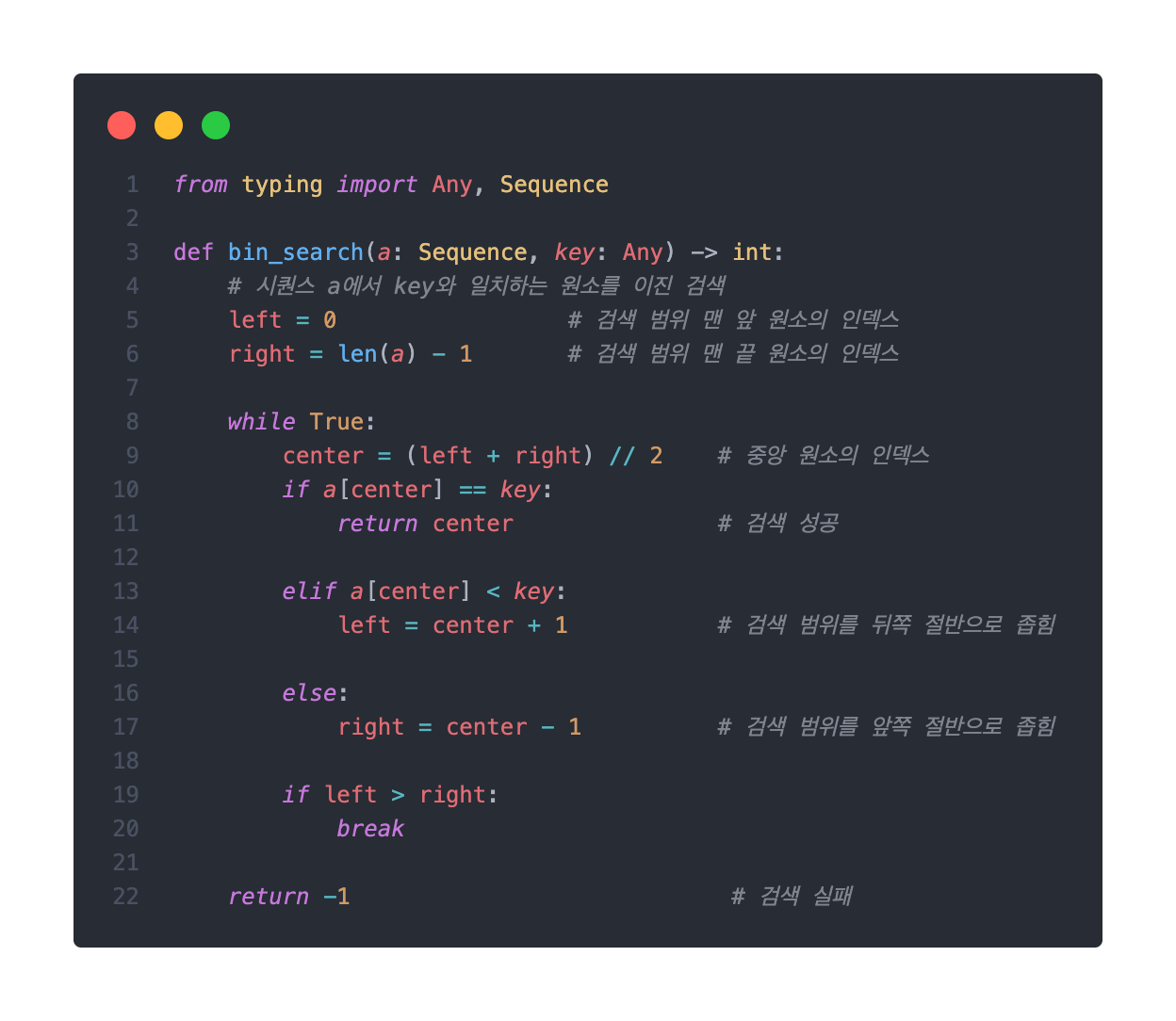
- 중간값이 키값과 일치할 경우(
a[center] == key) 해당 중간값의 인덱스를 리턴 - 검색 범위가 더이상 존재하지 않을 때(
left > right) -1 리턴
선형 검색과 비교
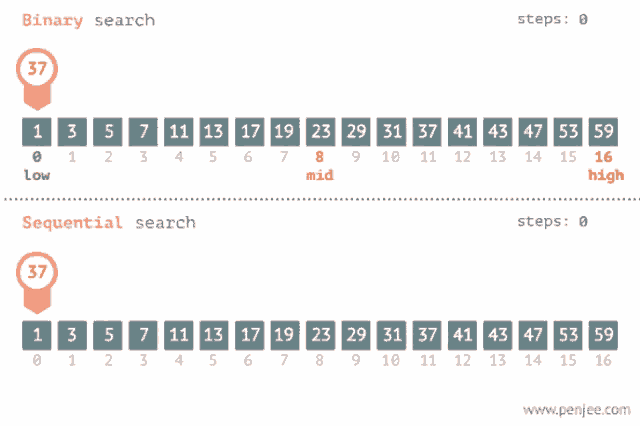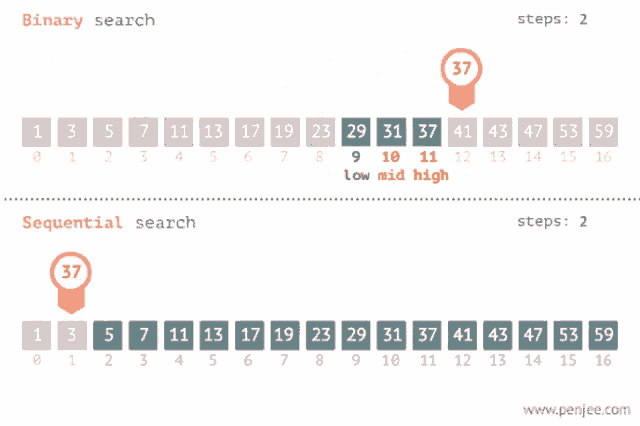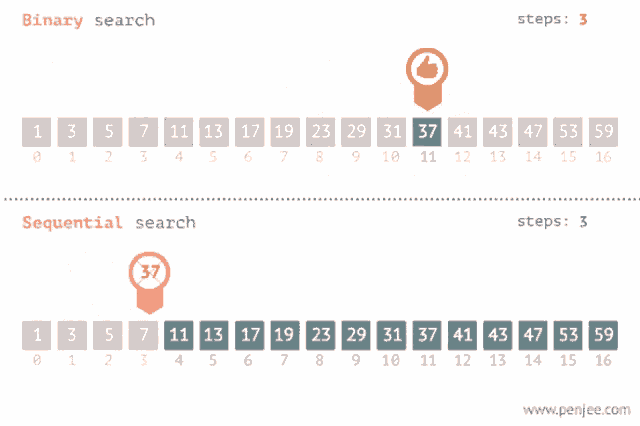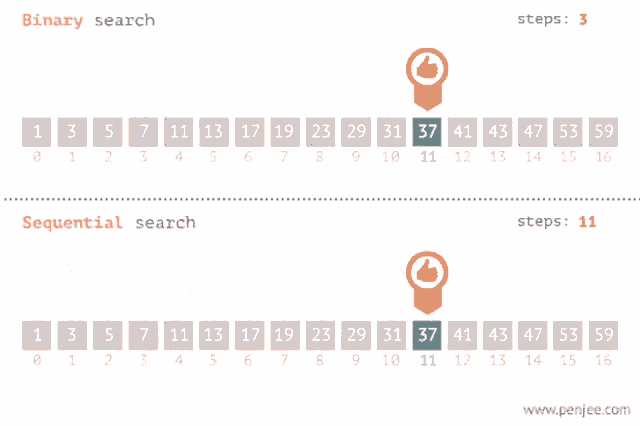
시간 복잡도
- 선형 검색
- 최악의 경우 마지막까지 탐색을 하기 때문에 시간 복잡도는
O(N)
- 최악의 경우 마지막까지 탐색을 하기 때문에 시간 복잡도는
- 이진 검색
- 배열의 크기를 N이라고 할 때, 첫 시행후엔 절반이 남으므로 N/2
- 두번째 시행 후에는 4/N
- N번째 시행 후에는 (1/2)k * N
- 최악의 경우에는 배열의 사이즈가 1이 될때까지 반으로 쪼개는 것이므로 (1/2)k * N = 1
- 이 때 양변에 log를 취하면 log2N
- 시간 복잡도는
O(logN)
정리
이진 검색의 경우 선형 검색보다 빠르지만, 배열이 정렬되어있어야 사용이 가능하다는 단점이 있다.
Take Away
시간 복잡도 비교
선형 탐색과 이진 탐색,
대표적인 두 탐색법을 알아봤고, 여기서 시간 복잡도라는 개념에 대해 진지하게 접하게 되었다.
시간 복잡도가 더 적을지라도 해당 방법이 어떤 특징과 장단을 알고 있는지 제대로 알고 넘어가야 추후 적용을 할 때 실수하지 않고 적재적소에 넣을 수 있을 것 같다.
어렵다 자료구조!
참고
https://www.geeksforgeeks.org/binary-search/
https://yoongrammer.tistory.com/75
https://steady-coding.tistory.com/229
https://velog.io/@jinatra/Linear-Search
