
트리
정의
데이터 사이의 계층 관계를 표현하는 비선형 계층적 자료구조
계층적인 자료를 표현하는데 이용되는 구조
나무를 거꾸로 해놓은 모양과 비슷해 Tree 구조라고 부른다
설명
그림
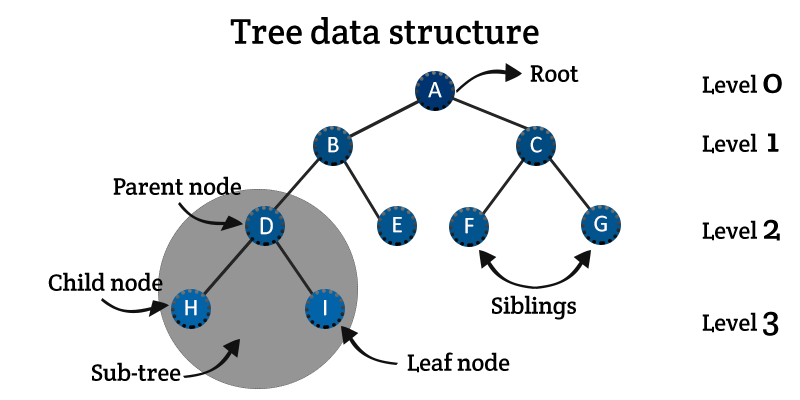
용어
- Node (노드)
- 트리를 구성하고 있는 기본 요소
- Key, Value, 혹은 하위 노드에 대한 포인터를 가지고 있음
- A, B, C, D, E 등..
- Edge (가지)
- 노드와 노드간의 연결선
- Root (루트)
- 트리의 가장 위쪽에 있는 노드
- 트리에 단 하나만 존재
- A
- Leaf (리프)
- 트리의 가장 아래쪽에 있는 노드
- H, I
- Parent Node (부모 노드)
- 어떤 노드와 가지가 연결되었을 때 가장 위쪽에 있는 노드
- 노드의 부모 노드는 하나만 존재
- 루트 노드는 부모 노드를 가지지 않음
- 노드 B, D, E의 부모 노드는 B
- Child Node (자식 노드)
- 어떤 노드와 가지가 연결되었을 때 아래쪽에 있는 노드
- 노드는 여러개의 자식 노드를 가질 수 있음
- 노드 B, D, E의 자식 노드는 D, E
- Sibling Node (형제 노드)
- 부모가 같은 노드
- 노드 B, D, E에서 D,E 노드는 형제 관계
- Level (레벨)
- 루트에서 얼마나 멀리 떨어져 있는지를 나타내는 수치
- 루트 노드는 Level 0
- 루트 노드로부터 가지가 하나씩 뻗어나갈 때마다 +1
- degree (차수)
- 각 노드가 갖는 자식의 수
- 노트 B는 D, E의 자식을 가지므로 차수가 2이다
- Sub tree (서브 트리)
- 어떤 노드를 루트로 하고, 그 자손으로 구성된 트리
- 그림의 검은 원에 포함된 부분은 노드D를 부모로 하는 서브 트리
탐색 방법
깊이 우선 탐색 (Depth First Search)
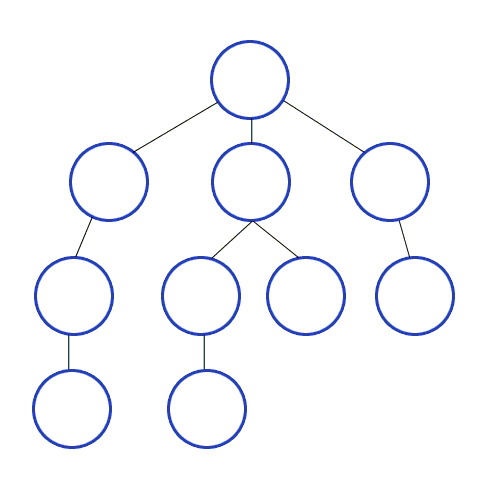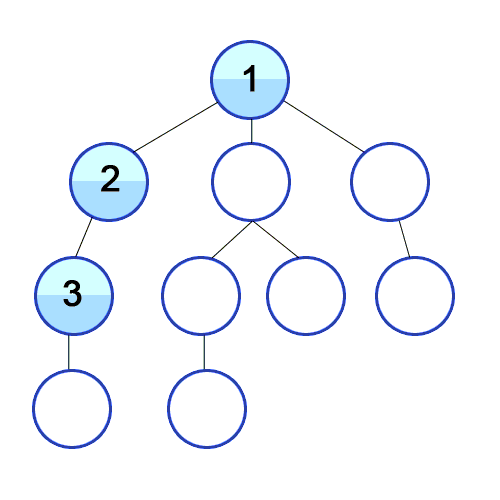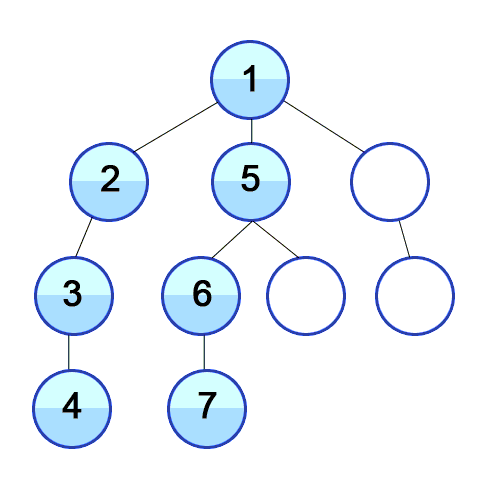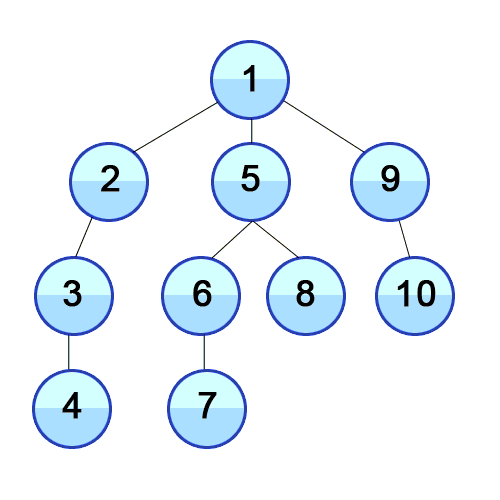
- 리프에 도달할 때까지 아래쪽으로 내려가면서 검색하는 것을 우선시
- 리프에 도달 후 더 이상 검색할 곳이 없으면 부모 노드로 복귀
- 이후 다시 자식 노드로 검색
너비 우선 탐색 (Breadth First Search)
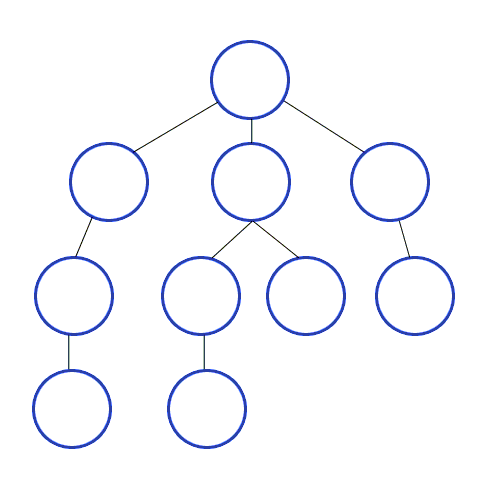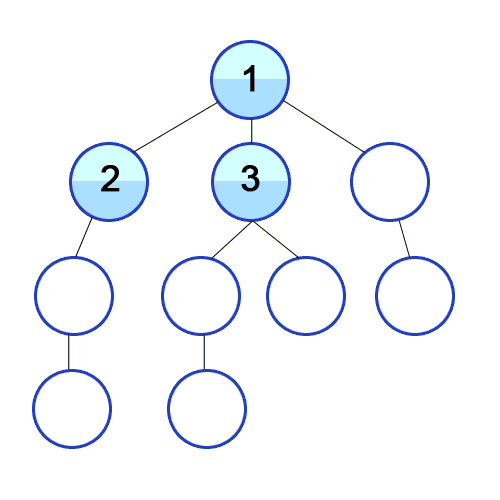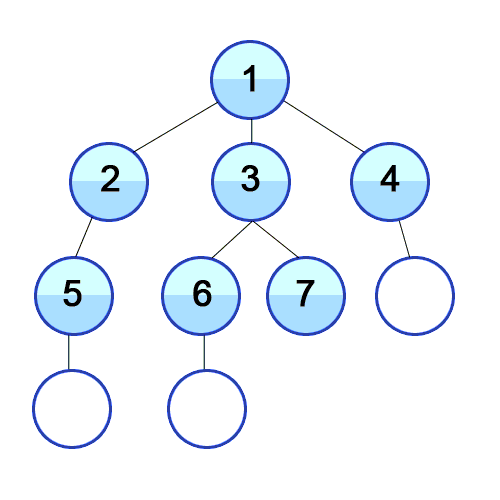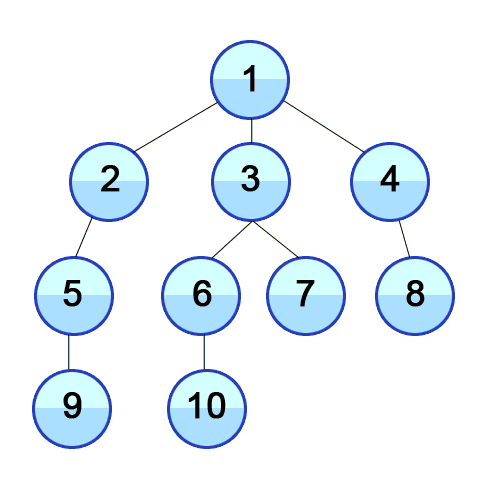
- 낮은 레벨부터 왼쪽에서 오른쪽으로 검색
- 한 레벨에서 검색을 마치면 다음 레벨로 내려가 동일한 방법 반복
비교
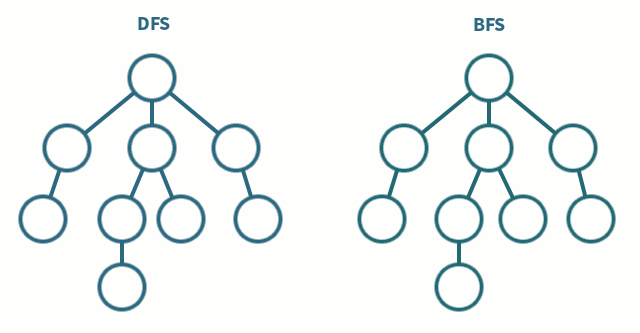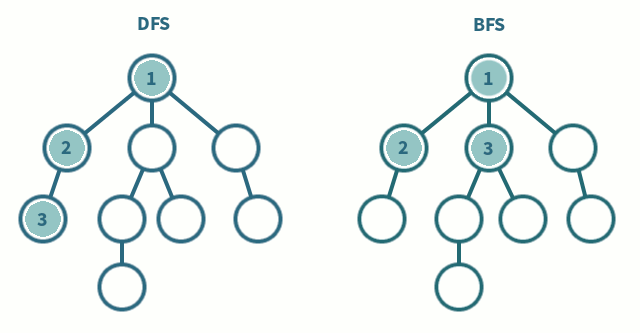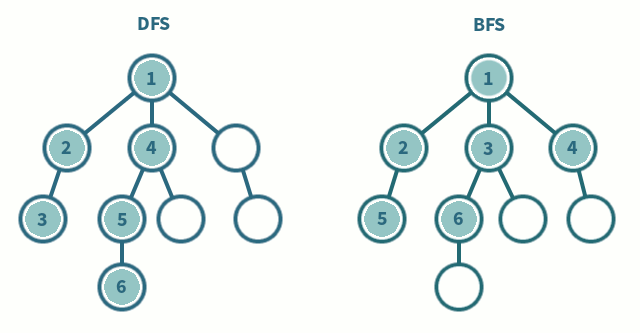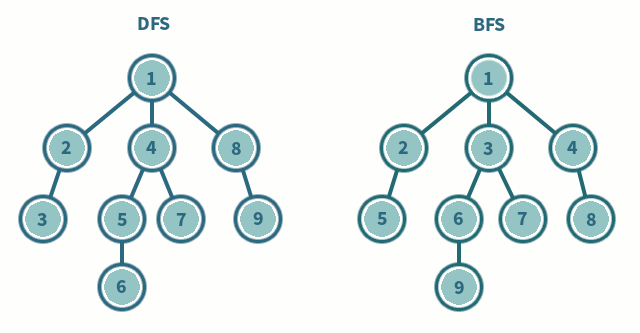
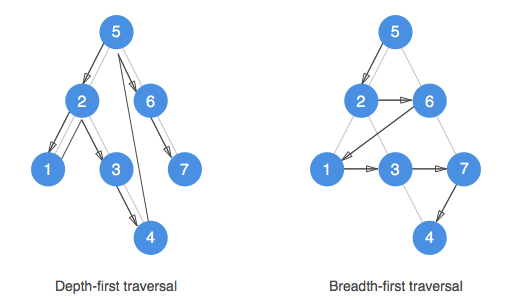
- 깊이 우선 탐색 (DFS)
- 모든 노드를 탐색하고자 할 때 사용
- 너비 우선 탐색 (BFS)보다 간단
- 단순 검색 속도는 너비 우선 탐색(BFS)보다 느림 (모든 노드를 탐색해야 하기에)
- 스택(Stack) 또는 재귀 함수를 이용하여 구현
- 시간 복잡도: O(|V|+|E|)
- V: 노드 개수
- E: 가지 개수
- 너비 우선 탐색 (BFS)
- 두 노드 사이의 최단 경로 또는 임의의 경로를 탐색하고자 할 때 사용
- 재귀적으로 동작 X
- 큐(Que)를 이용하여 구현
- 시간 복잡도: O(|V|^2)
- V: 노드 개수
순회
전위 순회 (preorder traversal)
노드 방문 → 왼쪽 자식 → 오른쪽 자식
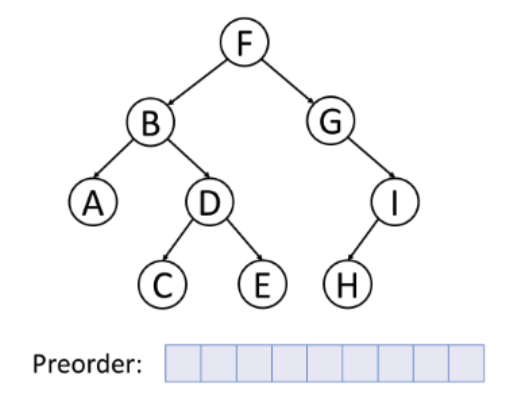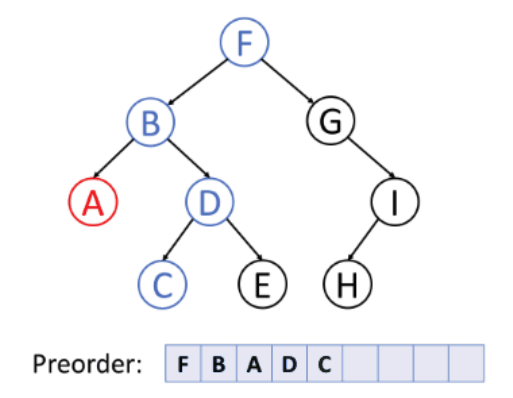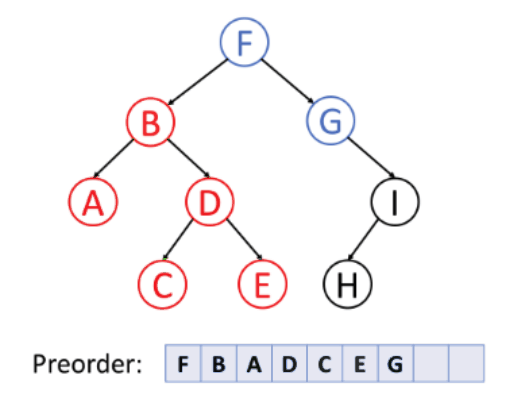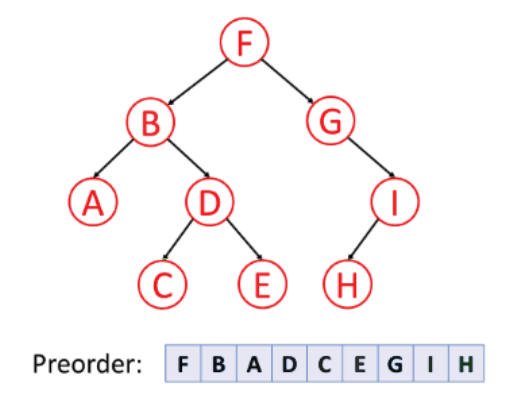
중위 순회 (inorder traversal)
왼쪽 자식 → 노드 방문 → 오른쪽 자식
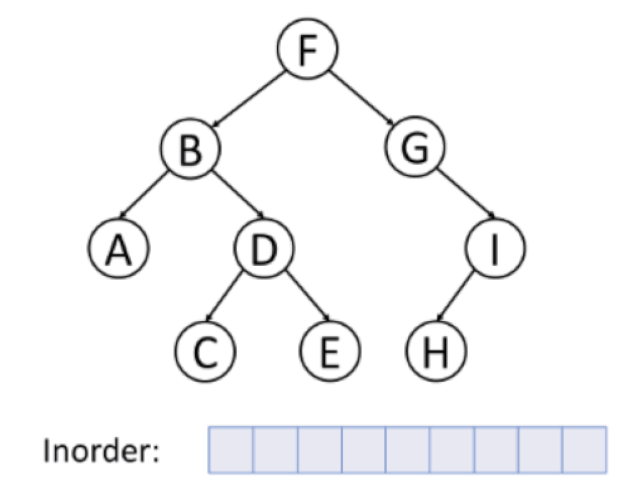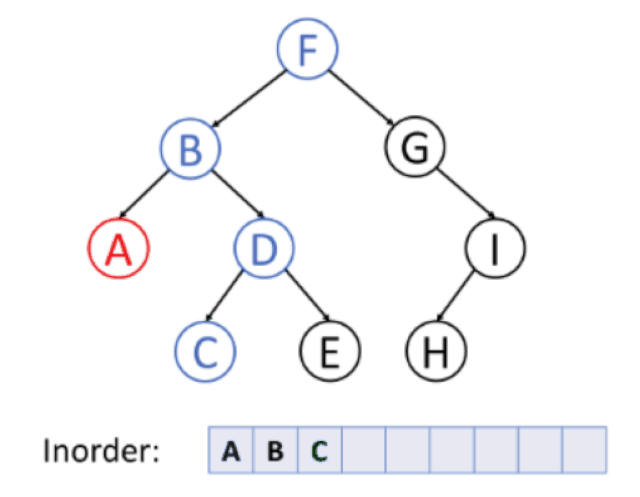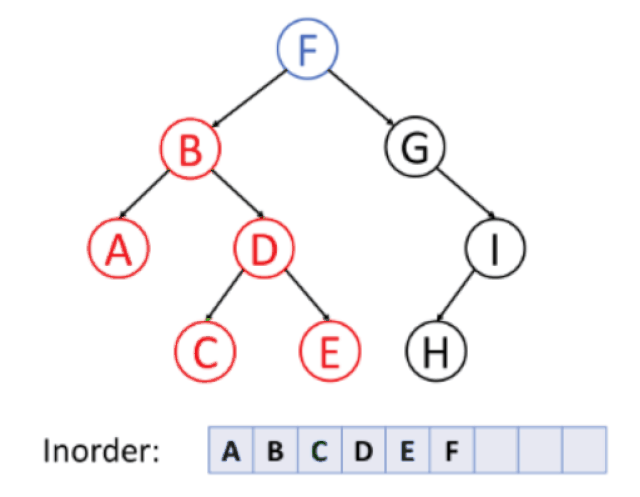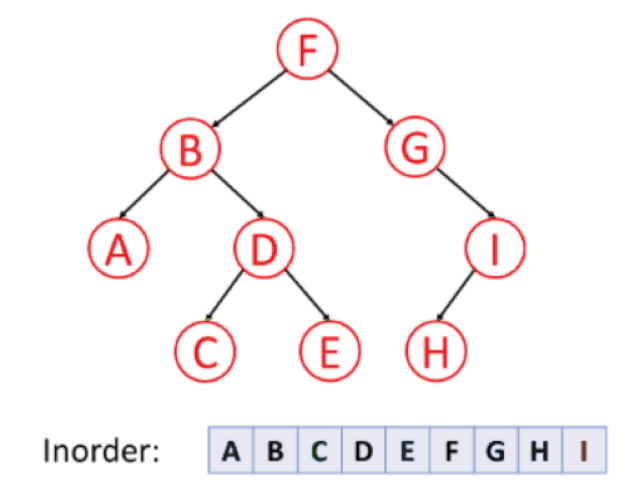
후위 순회 (postorder traversal)
왼쪽 자식 → 오른쪽 자식 → 노드 방문
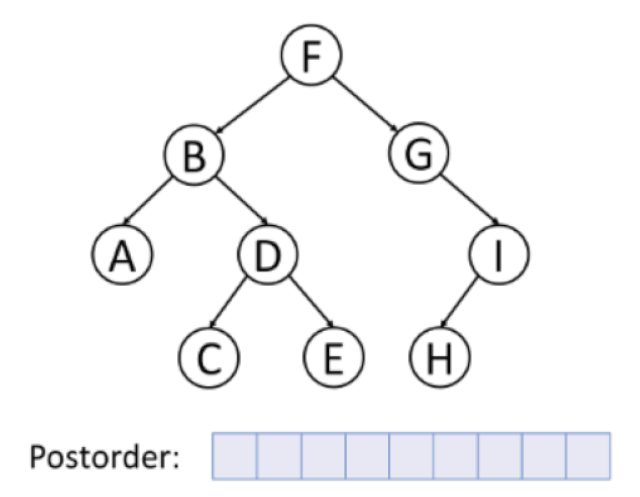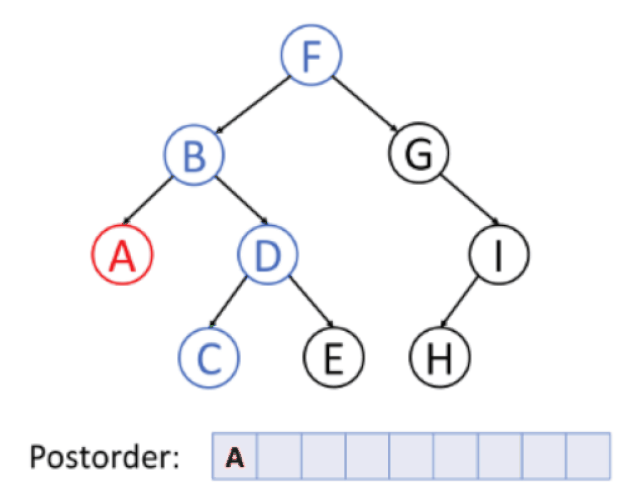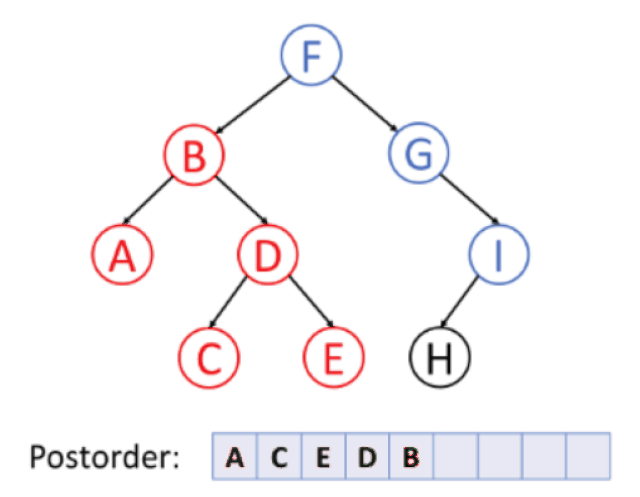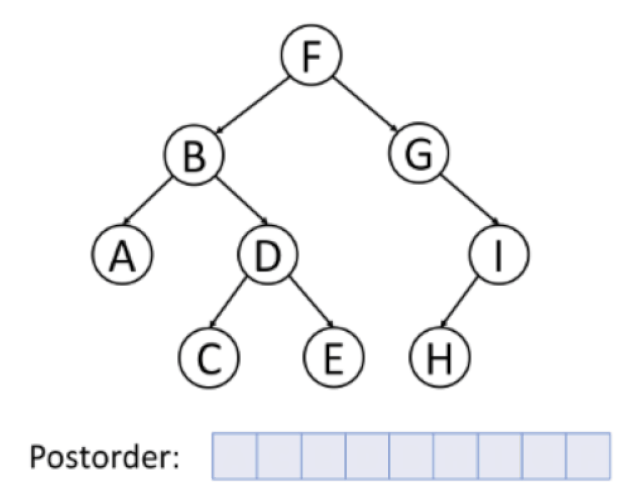
Take Away
DFS vs. BFS
트리 자체는 쉬운 개념이지만, 여기서 나오는
DFS(깊이 우선 탐색) / BFS(너비 우선 탐색)
두 개념을 차이점을 알아두는게 중요할 것 같다.
나중에 탐색 알고리즘을 짜게 된다면 반드시 고려해야할 사항이지 않을까?
참고
https://commons.wikimedia.org/wiki/Main_Page
https://nick.balestrafoster.com/2015/depthFirst-vs-breadthFirst/
https://velog.io/@lucky-korma/DFS-BFS의-설명-차이점
https://yunyoung1819.tistory.com/86
