[위상 정렬] ACM CRAFT(백준) - DFS 시간초과=>메모제이션 추가 / + 위상정렬 풀이법

위상 정렬(Topology sort)

reference: https://m.blog.naver.com/ndb796/221236874984

• 순서가 정해져 있는 작업을 차례로 수행해야할 때 그 순서를 결정해주는 알고리즘
• ex) 선후수 과목 리스트에서 특정 과목 수강신청까지의 경로(수업)
• ex) 스타크래프트 빌드 시나리오에서 특정 건물을 올리기까지의 경로(빌드)

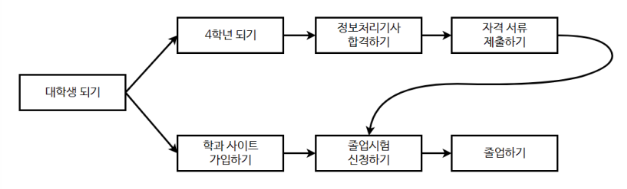
해 1: '대학생 되기' -> '4학년 되기' -> '정보처리기사 합격하기' -> '자격 서류 제출하기' -> '학과 사이트 가입하기' -> '졸업시험 신청하기' -> '졸업하기'

해 2: '대학생 되기' -> '학과 사이트 가입하기' -> '4학년 되기' -> '정보처리기사 합격하기' -> '자격 서류 제출하기' -> '졸업시험 신청하기' -> '졸업하기'

해 3: ...

위상정렬 문제는 여러 개의 답이 존재할 수 있다.

위상 정렬 조건
위상 정렬은 DAG(Directed Acyclic Graph), 즉 '사이클이 발생하지 않는 방향 그래프'에만 적용할 수 있다.

큐를 사용한 위상 정렬 알고리즘 구현

1) 진입차수가 0인 정점을 큐에 삽입 

while(!q.empty()) {

	2) 큐에서 원소를 꺼내 연결된 모든 간선을 제거
	3) 간선 제거 후 진입차수가 0이 된 정점을 큐에 삽입
    
}

// 모든 원소를 방문하였다면 큐에서 꺼낸 순서가 위상 정렬의 결과!

// 진입차수가 0인 정점이 여러 개 있을 때 큐에 넣는 순서에 따라, 간선을 제거하는 순서에 따라 여러 답이 존재할 수 있다. 

---

예제 문제: ACM Craft_백준

source: https://www.acmicpc.net/problem/1005

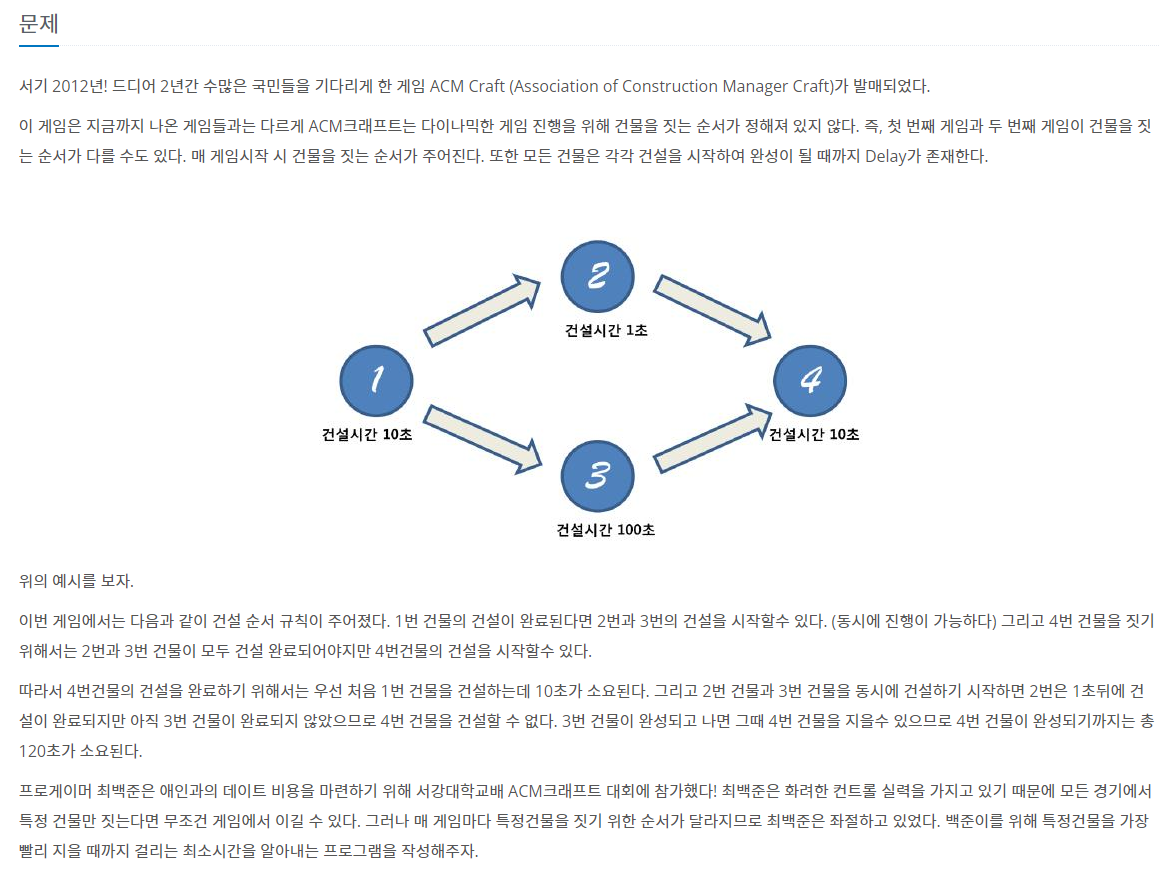
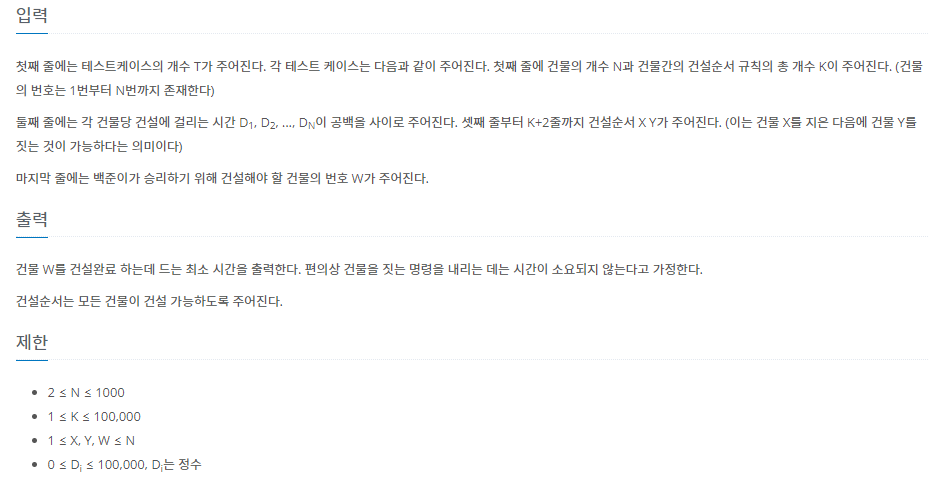
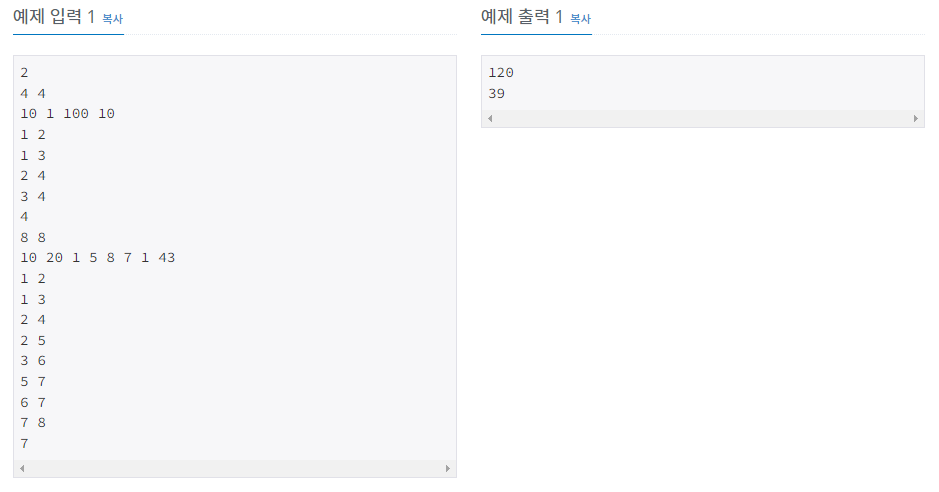
DFS + 메모제이션 풀이법

#include <bits/stdc++.h>
using namespace std;

int t, n, k, w;
int nArr[1000+1];
vector<int> pArr[1000+1];
int totalCount;
vector<long long> totalResult;
long long dp[1000+1];


long long dfs(int nodeName){
    // memozation 활용		<= 메모제이션을 안한다면 시간초과뜸. 
    if(dp[nodeName] != -1){
        return dp[nodeName];
    }

    // 종료 조건
    if(pArr[nodeName].size() == 0){
        return nArr[nodeName];
    }

    long long _max = dfs(pArr[nodeName][0]);
    for(int i=1; i<pArr[nodeName].size(); i++){     
        _max = max(_max, dfs(pArr[nodeName][i]));
    }

    // 메모제이션
    dp[nodeName] = nArr[nodeName] + _max;
    return dp[nodeName];
}

int main(){
    cin >> t;
    for(int tt=0; tt<t; tt++){    

        cin >> n >> k;

        for(int i=1; i<=n; i++){    // O(n*clear시간복잡도) // clear 시간 복잡도: O(1)?
            pArr[i].clear();
        }
        //dp 초기화
        for(int i=0; i<=n; i++){    // O(n)
            dp[i] = -1;             // -1로 초기화하는 이유는 시간이 0인 경우도 있기에
        }			    // 처음에 이를 고려하지 못했음. 따라서 당연히 실패 

        for(int i=1; i<=n; i++){
            int x;
            cin >> x;
            nArr[i] = x; 
        }
        for(int i=0; i<k; i++){
            int x, y;
            cin >> x >> y;
            pArr[y].push_back(x);   // x => y로 연결
                                    // pArr은 y로 오기 이전의 경로들의 집합(벡터로 묶음)
        }

        cin >> w;

       long long result = dfs(w);
        totalResult.push_back(result);
    }

    for(int i=0; i<totalResult.size(); i++){
        cout << totalResult[i] << '\n';
    }
}

위상정렬 풀이법

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

// 위상정렬
int topicalSort(vector<int>& originBuildTime, vector<int>& buildTime, vector<vector<int>>& nextBuild, vector<int>& indegree, int n, int w) {

	// 노드 진입차수가 0인 노드들을 큐에 담는다.
	queue<int> readyQueue;
	for (int i = 1; i <= n; i++) {
		if (indegree[i] == 0)
			readyQueue.push(i);
	}

	while (!readyQueue.empty()) {
		// 진입차수가 0인 것들을 하나씩 꺼내가며 건물을 만들어간다. 
		int nowNode = readyQueue.front(); readyQueue.pop();
        
		// 목표 건물이라면,
		if (nowNode == w) {
			return buildTime[w];
		}

		// 현재 노드의 다음 빌드를 탐색
		int len = nextBuild[nowNode].size();
		for (int i = 0; i < len; i++) {
			int nextNode = nextBuild[nowNode][i];
			indegree[nextNode]--;

			if (indegree[nextNode] == 0)
				readyQueue.push(nextNode);

			// 건설 시간 합
            // 큰 값을 선택해야 한다. 
			buildTime[nextNode] = max(buildTime[nextNode], originBuildTime[nextNode] + buildTime[nowNode]);
		}
	}

	// 목표 건축물을 짓지 못함
	return -1;
}

int main() {
	int testCase;
	cin >> testCase;

	vector<int> results;
	for (int t = 0; t < testCase; t++) {
		int n, k;	// n: 건물의 갯수, k: 규칙의 갯수
		cin >> n >> k;
		
		// 건물 건축 기간
		vector<int> buildTime(n + 1);
		vector<int> originBuildTime(n + 1);
		for (int i = 1; i <= n; i++) {
			int x;
			cin >> x;
			buildTime[i] = x;
			originBuildTime[i] = x;
		}

		// 후수 조건
		vector<vector<int>> nextBuild(n + 1);
		// 노드 진입차수
		vector<int> indegree(n + 1, 0);

		for (int i = 0; i < k; i++) {
			int a, b;	// a->b
			cin >> a >> b;
			nextBuild[a].push_back(b);
			indegree[b]++;
		}

		// 목적 건물 w
		int w;
		cin >> w;

		// 위상정렬 함수
		// int topicalSort(vector<int>& originBuildTime, vector<int>& buildTime, vector<vector<int>>& nextBuild, vector<int>& indegree, int n, int w) 
		int result = topicalSort(originBuildTime, buildTime, nextBuild, indegree, n, w);

		//cout << result << endl;
		results.push_back(result);

	}

	for (int i = 0; i < results.size(); i++) {
		cout << results[i] << endl;
	}

	return 0;
}