[위상 정렬] 개념과 예제 문제: 문제집_백준

위상정렬

위상 정렬(topology sort)은 정렬 알고리즘의 일종.
순서가 정해져 있는 일련의 작업을 차례대로 수행해야 할 때 사용할 수 있는 알고리즘.

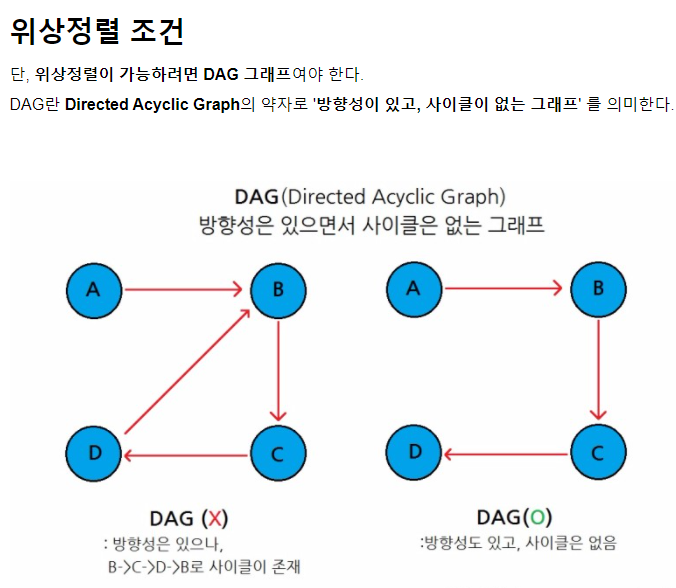
위상 정렬이란 방향 그래프의 모든 노드를 '방향성에 거스르지 않도록 순서대로 나열하는 것

전형적인 예시로는 '선수과목'을 고려한 학습 순서 설정을 들 수 있다.

source: https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html

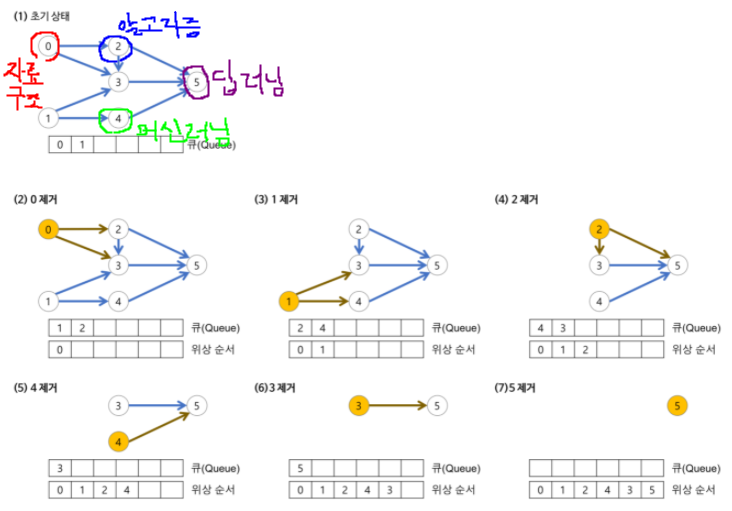
진입차수란? 특정한 노드로 '들어오는' 간선의 갯수
위 그림에서 0번 노드의 진입차수는 0, 3번 노드의 진입차수는 3이다.

위상 정렬 알고리즘의 프로세스는 다음과 같다.
1. 진입차수가 0인 노드를 큐에 넣는다.
2. 큐가 빌 때까지 다음을 반복한다.
1) 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다.
2) 새롭게 진입차수가 0인 된 노드를 큐에 넣는다.

위 프로세스에서 모든 원사를 방문하기 전에 큐가 비어버리면 사이클이 발생한 것이다.

_

source: https://gmlwjd9405.github.io/2018/08/27/algorithm-topological-sort.html

---

위상 정렬 c++ 코드

#include <bits/stdc++.h>
using namespace std;

// 노드의 갯수 v
// 간선의 갯수 e
int v, e;

// 모든 노드에 대한 진입차수는 0으로 초기화
int indegree[100001];

// 각 노드에 연결된 간선 정보를 담기위한 연결 리스트
vector<int> graph[100001];

void topologySort(){
    vector<int> result;
    queue<int> q;

    // 초기화
    // 진입차수가 0인 모든 노드를 큐에 삽입
    for(int i=1; i<=v; i++){
        if(indegree[i] == 0)
            q.push(i);
    }


    //
    while(!q.empty()){
        int now = q.front(); q.pop();

        result.push_back(now);

        // 해당 원소와 연결된 노드의 진입차수 1 빼기
        for(int i=0; i<graph[now].size(); i++){
            int next = graph[now][i];

            // 진입차수 빼기
            indegree[next]--;

            // 만약 해당 노드가 진입차수가 0이라면 큐에 삽입
            if(indegree[next] == 0)
                q.push(next);
        }
    }

    // 사이클 유무 확인
    if(result.size() != v){
        cout << "사이클 생성" << '\n';
        return;
    }
    else{
        cout << "위상 정렬 후" << '\n';
        for(int i=0; i<result.size(); i++){
            cout << result[i] << ' ';
        }
        cout << '\n';
    }

}

int main(){
    cin >> v >> e;

    // 방향 그래프의 모든 간선 정보를 입력 받기
    for(int i=0; i<e; i++){
        int a, b;   // a -> b
        cin >> a >> b;  
        graph[a].push_back(b);  // a -> b

        // 진입 차수를 1 증가
        indegree[b] += 1;
    }    
    

    // 위상 정렬
    topologySort();
}

---

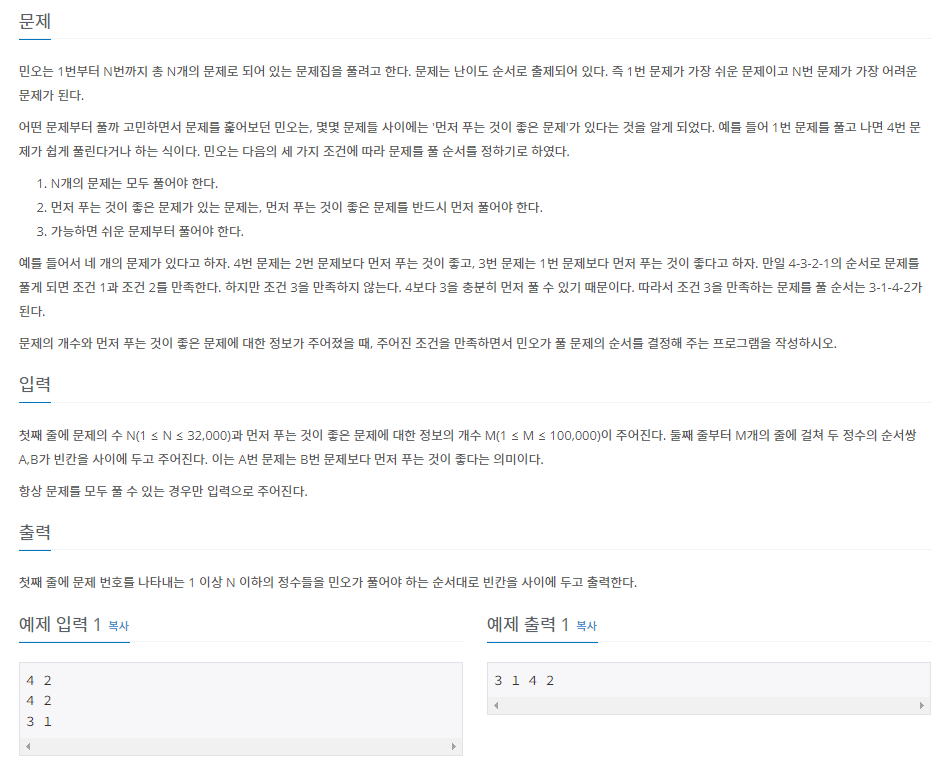
예제 문제: 문제집_백준

source: https://www.acmicpc.net/problem/1766

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

void topologySort(int n, vector<vector<int>> &graph, vector<int> &indegree) {
	
	// 처리해야할 문제에 대한 큐를 만든다. 
	// 처리해야할 조건은 일단 문제번호가 낮은 것부터 풀어야 한다.
	// 우선순위 큐가 적절한 것으로 보인다. 
	priority_queue<int> pq;	// 내림차순 정렬
	vector<int> answer;

	// 진입차수가 0인 것을 기준으로 초기화한다.
	for (int i = 1; i <= n; i++) {
		if (indegree[i] == 0) {
			pq.push(-i);	// 음수로 push해야 작은 것부터 pop 된다.
		}
	}

	while (!pq.empty()) {
				// 주의, 다시 양수로 뽑아야함. 
		int nowNum = -pq.top(); pq.pop();

		answer.push_back(nowNum);
       
		// 연결된 노드 확인
		for (int i = 0; i < graph[nowNum].size(); i++) {
			int nextNum = graph[nowNum][i];
			
			// 연결된 노드의 진입차수 감소
			indegree[nextNum]--;

			// 해당 노드의 진입차수가 0이면 pq에 push
            if(indegree[nextNum] == 0)
			    pq.push(-nextNum);
		}
	}

	for (int i = 0; i < n; i++) {
		cout << answer[i] << ' ';
	}
	cout << '\n';
}


int main() {
	ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);


	int n, m;
	cin >> n >> m;


	// 지역에 큰 배열을 선언하면 메모리 초과?!?!?!?

	// 그래프 정보
	vector<vector<int>> graph(n+1);	// 1~n개의 문제
	// 진입차수 정보
	vector<int> indegree(n + 1, 0);


	// 순서 정보
	for (int i = 0; i < m; i++) {
		int a, b;	// a -> b 순서로 하는 것이 적절
		cin >> a >> b;

		// 그래프 정보 갱신
		graph[a].push_back(b);
		// 진입차수 갱신
		indegree[b]++;
	}

	topologySort(n, graph, indegree);
	
	return 0;
}