[다익스트라] 다익스트라 응용(최적 경로 추적, 특정 간선 제외 경로) 예제 문제: 도로 검문_백준

도로 검문_백준

source: https://www.acmicpc.net/problem/2307

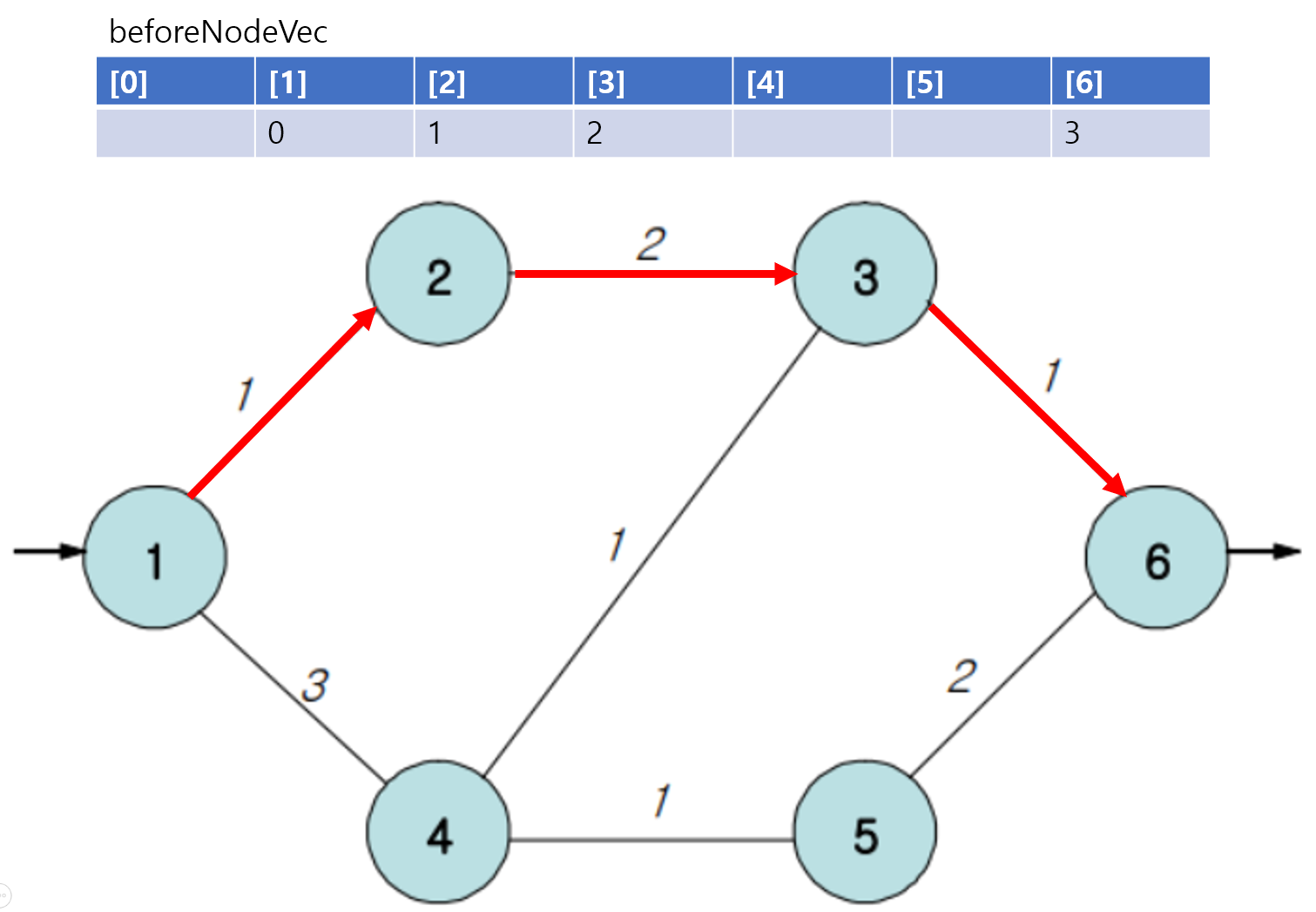
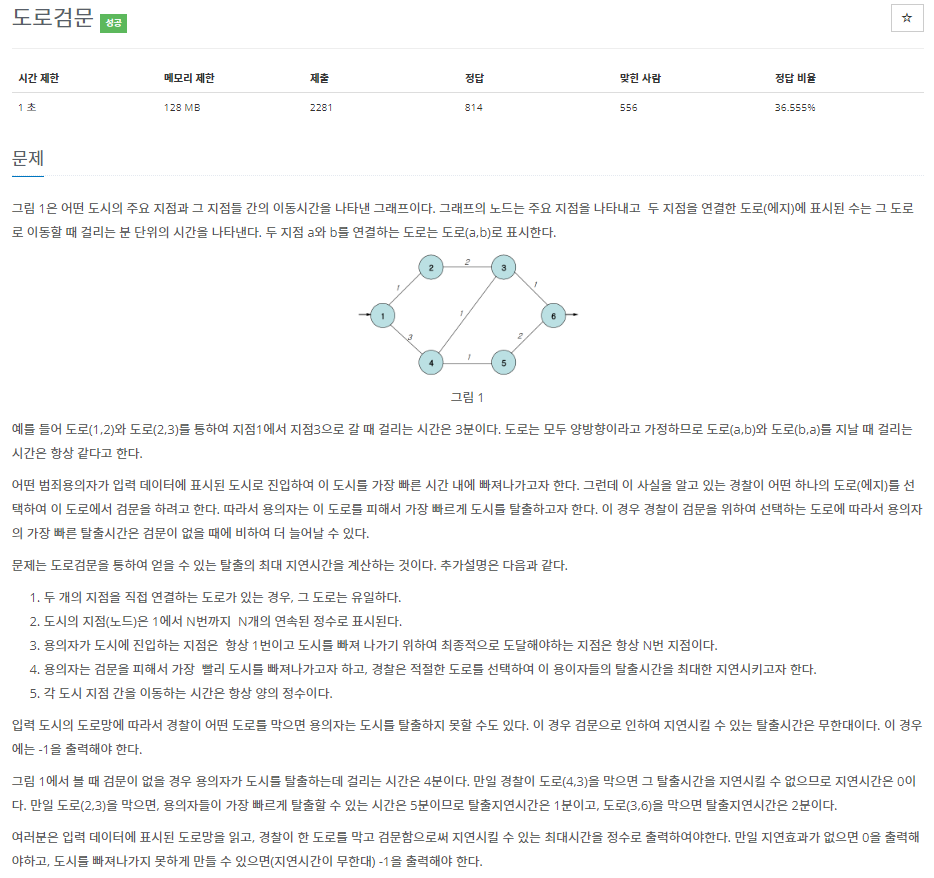
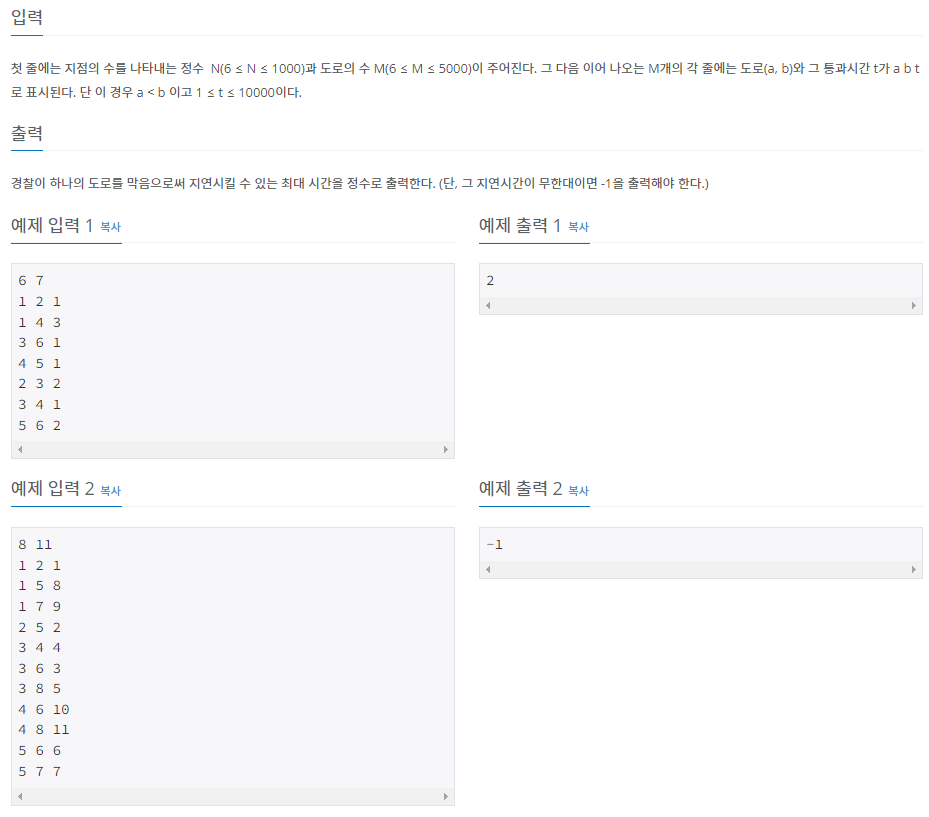
(1) 경찰이 없을 때 도둑의 최적 경로 찾기

(2) 도둑의 경로(도착지->출발지)를 (1) 찾은 후,
해당 경로에서 하나의 간선을 빼가면서 각각 다익스트라로 최단거리 구한다. 그리고 각각 구한 것 중 최대 값이 지연시간이 가장 많이 추가된 경로이다.

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct cmp {
	bool operator() (const pair<pair<int, int>, int>& p1, const pair<pair<int, int>, int>& p2){
		return p1.first.second > p2.first.second;
	}

	bool operator() (const pair<int, int>& p1, const pair<int, int>& p2) {
		return p1.second > p2.second;
	}
};

int N, M;	// 도시의 수, 도로의 수
vector<vector<pair<int, int>>> graph(1000 + 1);

bool checkPoint(int nowNode, int nextNode, int checkLoc1, int checkLoc2) {
	if (nowNode == checkLoc1 && nextNode == checkLoc2)
		return true;
	else if (nowNode == checkLoc2 && nextNode == checkLoc1)
		return true;
	else
		return false;
}

int solution() {
	// (1) 검문이 없을 때 도둑의 최적 경로 찾기
	// O( M*logN )

	// 경로 추적을 위한 벡터
	vector<int> beforeNodeVec(N + 1, 0);	// beforeNode[after] = before;
	// 최단거리 테이브
	vector<int> minDist(N + 1, 1e9);

	// pair<pair<int, int>, int> : <<다음 노드, 비용>, 이전 노드>
	priority_queue<pair<pair<int, int>, int>, vector<pair<pair<int, int>, int>>, cmp> pq;
	// 시작 노드(1)의 주변 노드 넣기
	for (int i = 0; i < graph[1].size(); i++) {
		pq.push({ graph[1][i], 1 });
		minDist[graph[1][i].first] = graph[1][i].second;
	}
	while (!pq.empty()) {
		pair<pair<int, int>, int> p = pq.top(); pq.pop();
		int nowNode = p.first.first;
		int nowCost = p.first.second;
		int beforeNode = p.second;

		if (minDist[nowNode] < nowCost)
			continue;

		// 경로 추적 벡터 추가
		beforeNodeVec[nowNode] = beforeNode;

		// nowNode의 주변 노드 새로 담기
		for (int i = 0; i < graph[nowNode].size(); i++) {
			int nextNode = graph[nowNode][i].first;
			int nextCost = graph[nowNode][i].second + nowCost;

			if (minDist[nextNode] > nextCost) {
				pq.push({ { nextNode, nextCost }, nowNode });
				minDist[nextNode] = nextCost;
			}
		}
	}
	// 검문이 없을 때의 소모 시간
	int minTime_withoutCheckPoint = minDist[N];



	// (2) 도둑의 경로 (도착지 -> 출발지)를 (1)에서 찾은 후 
	// 해당 경로에서 하나의 간선을 빼가면서 각각 다익스트라로 최단거리 구하기
	// 각각 구한 것 중 최대 값이 지연시간이 가장 많이 추가된 경로이다. 
	int maxTime_withCheckPoint = 0;
	int nowLoc = N;
	while (true) {
		//cout << "now: " << nowLoc << ", " << "before: " << beforeNodeVec[nowLoc] << endl;
		int beforeLoc = beforeNodeVec[nowLoc];
	
		// nowLoc <-> beforeLoc 을 거쳐가는 경로가 없도록 한다.
		// 해당 경로를 제외했을 떄 가장 지연도가 큰 값을 구한다. 
		// 최단거리 테이브
		vector<int> minDist(N + 1, 1e9);

		// pair<pair<int, int>, int> : <<다음 노드, 비용>, 이전 노드>
		priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pq;
		// 시작 노드(1)의 주변 노드 넣기
		for (int i = 0; i < graph[1].size(); i++) {
			if (checkPoint(nowLoc, beforeLoc, 1, graph[1][i].first))
				continue;
			pq.push(graph[1][i]);
			minDist[graph[1][i].first] = graph[1][i].second;
		}
		while (!pq.empty()) {
			pair<int, int> p = pq.top(); pq.pop();
			int nowNode = p.first;
			int nowCost = p.second;

			if (minDist[nowNode] < nowCost)
				continue;


			// nowNode의 주변 노드 새로 담기
			for (int i = 0; i < graph[nowNode].size(); i++) {
				int nextNode = graph[nowNode][i].first;
				int nextCost = graph[nowNode][i].second + nowCost;

				if (checkPoint(nowLoc, beforeLoc, nowNode, nextNode))
					continue;

				if (minDist[nextNode] > nextCost) {
					pq.push({ nextNode, nextCost });
					minDist[nextNode] = nextCost;
				}
			}
		}



		maxTime_withCheckPoint = max(maxTime_withCheckPoint, minDist[N]);


		if (beforeLoc == 1)
			break;
		else
			nowLoc = beforeNodeVec[nowLoc];
	}
	

	// 도둑의 최적의 경로에서 하나이 경로씩 막아보며 지연시간 최대값 구하기
	// O( M` * M*logN )

	if (maxTime_withCheckPoint == 1e9)
		return -1;

	return maxTime_withCheckPoint - minTime_withoutCheckPoint;
}

int main() {
	cin >> N >> M;

	for (int i = 0; i < M; i++) {
		int a, b, cost;
		cin >> a >> b >> cost;

		graph[a].push_back({ b, cost });
		graph[b].push_back({ a, cost });
	}

	int answer = solution();
	cout << answer << '\n';

	return 0;
}