[다익스트라] 다익스트라 응용 예제 문제: 중량제한_백준, 도로포장_백준

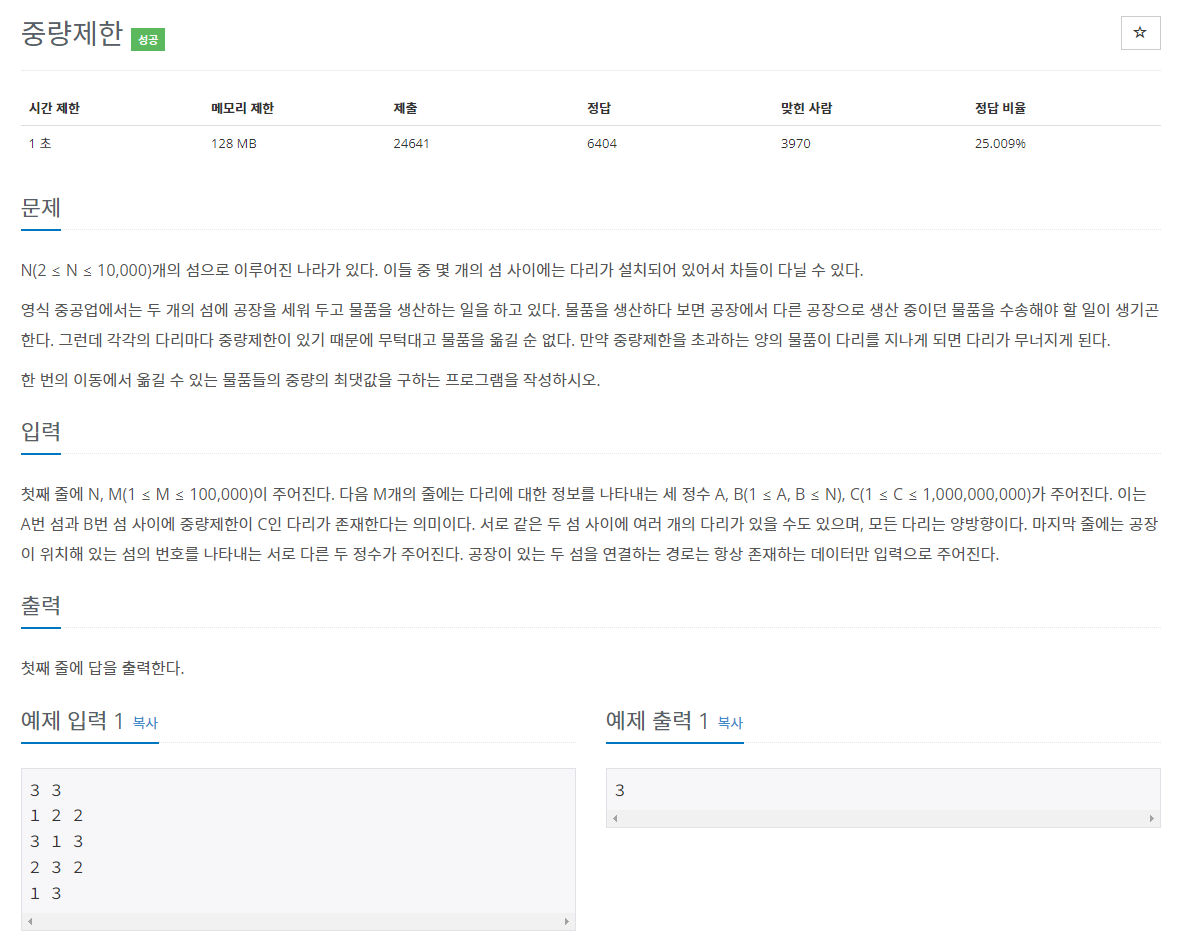
중량제한_백준

source: https://www.acmicpc.net/problem/1939

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct cmp {
	bool operator()(const pair<pair<int, int>, int>& p1, const pair<pair<int, int>, int>& p2) {
		return p1.second < p2.second;	// 비용이 큰 것부터 pop
	}
};

int N, M;
int S, E;
vector<vector<pair<int, int>>> graph(100000 + 1);

int solution() {
	int minWeight = 1e9;

	vector<int> visited(N + 1, 0);

	priority_queue<pair<pair<int, int>, int>, vector<pair<pair<int, int>, int>>, cmp> pq;

	// S번 노드의 이웃노드를 pq에 push
	visited[S] = 0;
	for (int i = 0; i < graph[S].size(); i++) {
		//pq.push({ graph[S][i].first, graph[S][i].second });
		pair<int, int> p = graph[S][i];
		int nextLoc = p.first;
		int nextCost = p.second;
		int minCost = p.second;
		
		//visited[nextLoc] = minCost;
		pq.push({ {nextLoc, nextCost}, minCost });
	}

	while (!pq.empty()) {
		pair<pair<int, int>, int> now = pq.top(); pq.pop();
		int nowLoc = now.first.first;
		int nowCost = now.first.second;
		int minCost = now.second;

		if (nowLoc == E)
			return minCost;

		if (minCost < visited[nowLoc])
			continue;

		// 주변 노드탐색
		for (int i = 0; i < graph[nowLoc].size(); i++) {
			pair<int, int> next = graph[nowLoc][i];
			int nextLoc = next.first;
			int nextCost = next.second;
			
			if (visited[nextLoc] < min(nextCost, minCost)) {
				pq.push({ {nextLoc, nextCost}, min(nextCost, minCost) });
				visited[nextLoc] = min(nextCost, minCost);
			}
		}
	}
}

int main() {
	cin >> N >> M;
	
	for (int i = 0; i < M; i++) {
		int a, b, cost;
		cin >> a >> b >> cost;
		graph[a].push_back({ b, cost });
		graph[b].push_back({ a, cost });
	}

	cin >> S >> E;

	cout << solution() << endl;
	return 0;

}

2022/06/17 풀이

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

struct cmp {
	bool operator()(const pair<int, int>& p1, const pair<int, int>& p2) {
		// 중량 제한이 큰 것을 우선으로 한다.
		return p1.second < p2.second;
	}
};

int N, M;

int solution(const vector<vector<pair<int, int>>>& BRIDGES, int start, int destination) {
	// 다음에 지나갈 다리들을 담을 우선순위 큐
	// 중량제한이 큰 것을 우선으로 한다.
	priority_queue<pair<int, int>, vector<pair<int, int>>, cmp> pq;	// <다리를 통해 도달하는 목적지, 다리의 제한>

	// 특정 노드(섬)까지의 최대 제한 중량을 담는다.
	vector<int> maxLimit(N + 1, 0);

	// 시작 섬(start)에서 연결된 다리들을 먼저 pq에 삽입한다.
	for (int i = 0; i < BRIDGES[start].size(); i++) {
		pair<int, int> p = BRIDGES[start][i];
		pq.push(p);
		maxLimit[p.first] = p.second;
	}

	// 다익스트라
	while (!pq.empty()) {
		pair<int, int> p = pq.top();
		pq.pop();

		int nowNode = p.first;
		int bridgeLimit = p.second;

		if (nowNode == destination) 
			return maxLimit[nowNode];


		if (maxLimit[nowNode] > bridgeLimit)
			continue;

		// nextNode 주변 다리 넣기
		for (int i = 0; i < BRIDGES[nowNode].size(); i++) {
			pair<int, int> nextp = BRIDGES[nowNode][i];
			int nextNode = nextp.first;
			int nextBridgeLimit = nextp.second;
			int minBridgeLimit = min(bridgeLimit, nextBridgeLimit);

			if (maxLimit[nextNode] < minBridgeLimit) {
				pq.push({ nextNode, minBridgeLimit });
				maxLimit[nextNode] = minBridgeLimit;
			}
		}


	}
}

int main() {
	cin >> N >> M;
	
	vector<vector<pair<int, int>>> BRIDGES(N+1);
	for (int i = 0; i < M; i++) {
		int from, to, limit;
		cin >> from >> to >> limit;
		
		BRIDGES[from].push_back({ to, limit });
		BRIDGES[to].push_back({ from, limit });
	}

	int start, destination;
	cin >> start >> destination;

	int answer = solution(BRIDGES, start, destination);
	cout << answer << endl;
}

2022/08/31 풀이(최신)

#include <iostream>
#include <vector>
#include <queue>
#include <map>
using namespace std;

const int MAX_WEIGHT = 1e9;

int N, M;	// 섬(노드)의 갯수, 다리(간선)의 갯수
vector<vector<pair<int, int>>> graph(10000 + 1);
int START, END;

struct LoadInfo {
	int node;
	int BeforeMaxWeight;
};

struct  cmp {
	bool operator()(const LoadInfo& info1, const LoadInfo& info2) {
		// BeforeMaxWeight 내림차순
		return info1.BeforeMaxWeight < info2.BeforeMaxWeight;
	}
};

int solution() {
	// BFS + 우선순위큐 방식으로 최대 코스트의 간선만을 선택하는 방식으로 최적 해를 구한다.
	priority_queue<LoadInfo, vector<LoadInfo>, cmp> pq;
	LoadInfo startInfo = { START, MAX_WEIGHT };
	pq.push(startInfo);

	//vector<bool> visited(N + 1, false);
	//visited[START] = true;
	vector<vector<bool>> visited(N + 1, vector<bool>(N + 1, false));
	// 간선에 대한 visited


	while (!pq.empty()) {
		LoadInfo info = pq.top();
		pq.pop();

		int nowNode = info.node;
		int bMaxWeight = info.BeforeMaxWeight;

		if (nowNode == END)
			return bMaxWeight;

		// 주변 노드 탐색
		for (int i = 0; i < graph[nowNode].size(); i++) {
			int nextNode = graph[nowNode][i].first;
			int edgeWeight = graph[nowNode][i].second;
			//if (visited[nextNode])
			if (visited[nowNode][nextNode])
				continue;

			LoadInfo nextInfo = { nextNode, min(bMaxWeight, edgeWeight) };
			pq.push(nextInfo);
			//visited[nextNode] = true;
			visited[nowNode][nextNode] = true;
		}
	}
}

int main() {
	cin >> N >> M;

	map<pair<int, int>, int> edgeMap;
	for (int i = 0; i < M; i++) {
		int a, b, c;
		cin >> a >> b >> c;
		//graph[a].push_back({ b, c });
		//graph[b].push_back({ a, c });
		
		pair<int, int> p = { min(a, b), max(a, b) };
		if (edgeMap.find(p) == edgeMap.end())
			edgeMap.insert({ p, c });
		else {
			edgeMap[p] = max(edgeMap[p], c);
		}
	}

	for (auto iter = edgeMap.begin(); iter != edgeMap.end(); iter++) {
		int a = (*iter).first.first;
		int b = (*iter).first.second;
		int c = (*iter).second;
		graph[a].push_back({ b, c });
		graph[b].push_back({ a, c });
	}



	cin >> START >> END;

	int answer = solution();
	cout << answer << endl;
}

---

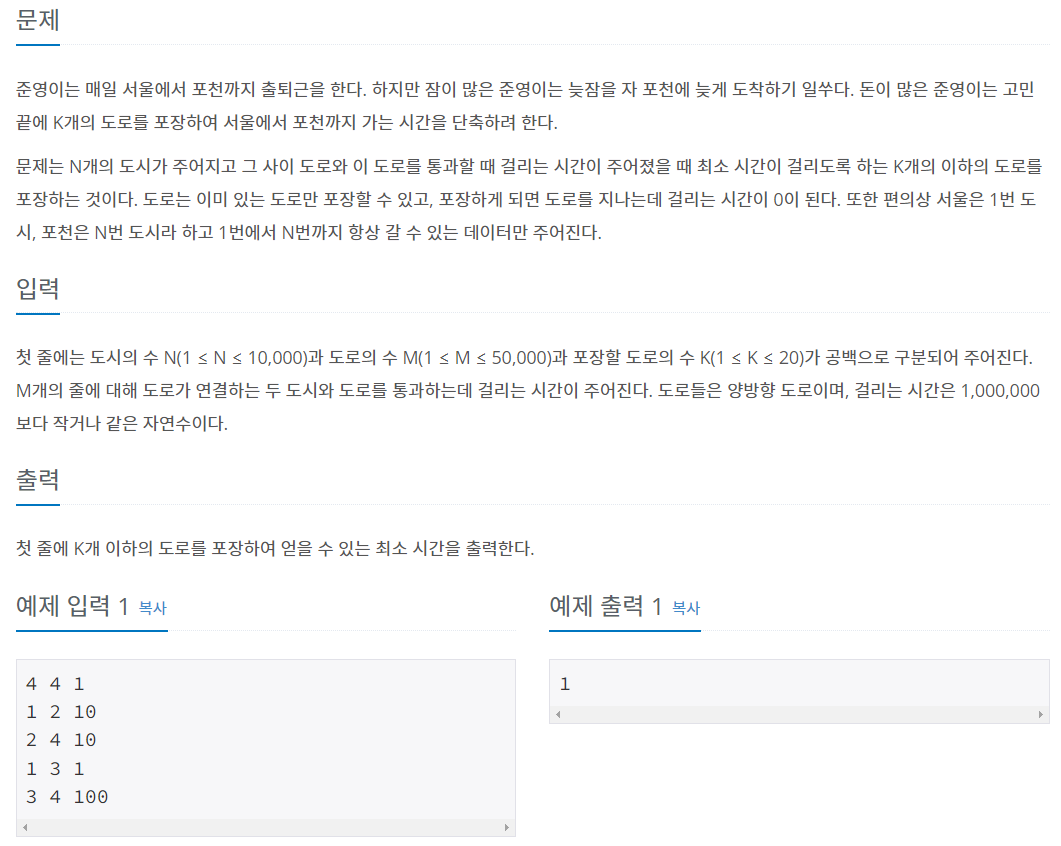
도로포장_백준

source: https://www.acmicpc.net/problem/1162

#include <iostream>
#include <vector>
#include <queue>

using namespace std;

struct cmp {
	bool operator()(const pair<pair<int, int>, long long>& p1, const pair<pair<int, int>, long long>& p2) {
		if (p1.second != p2.second)
			return p1.second > p2.second;
		else if (p1.first.second != p2.first.second)
			return p1.first.second < p2.first.second;
		else
			return p1.first.first < p2.first.first;
	}
};

int N, M, K;
vector<vector<pair<int, int>>> graph(10000 + 1);

long long solution() {
	int Start = 1;
	int End = N;
	// 특이케이스 처리
	if (N == 1)
		return 0;
	
				// <비용, 찬스>
	//vector<pair<long long, int>> minCostTable(N + 1, { 1e12, 0 });
	vector<vector<long long>> minCostTable(N + 1, vector<long long>(K + 1, 1e12));
	priority_queue<pair<pair<int, int>, long long>, vector<pair<pair<int, int>, long long>>, cmp> pq;
	
	// 시작점의 이웃노드들을 삽입
	//minCostTable[Start] = { -1, K };
	for (int i = 0; i <= K; i++) {
		minCostTable[Start][i] = 0;
	}
	for (int i = 0; i < graph[Start].size(); i++) {
		int nextNode = graph[Start][i].first;
		long long nextCost = graph[Start][i].second;

		// 다음 노드까지 도로를 포장하지 않음
		pq.push({ {nextNode, K}, nextCost });
		minCostTable[nextNode][K] = nextCost;
		pq.push({ { nextNode, K - 1 }, 0 });
		//minCostTable[nextNode] = { 0, K - 1 };
		minCostTable[nextNode][K - 1] = 0;

	}

	while (!pq.empty()) {
		pair<pair<int, int>, long long>  now = pq.top(); pq.pop();
		int nowNode = now.first.first;
		int resChance = now.first.second;
		long long nowCost = now.second;

		if (nowNode == End)
			return nowCost;

		// 백트래킹
		//if (nowCost > minCostTable[nowNode].first && resChance <= minCostTable[nowNode].second)
		//	continue;
		//else if (nowCost == minCostTable[nowNode].first && resChance < minCostTable[nowNode].second)
		//	continue;
		if (minCostTable[nowNode][resChance] < nowCost)
			continue;

		// 이웃노드탐색
		for (int i = 0; i < graph[nowNode].size(); i++) {
			int nextNode = graph[nowNode][i].first;
			long long nextCost = graph[nowNode][i].second;

			// 다음 노드까지 도로를 포장하지 않는다.
			//if (minCostTable[nextNode].first > nowCost + nextCost) {
			//	pq.push({ {nextNode, resChance}, nowCost + nextCost });
			//	// minCost 테이블도 갱신
			//	minCostTable[nextNode] = { nowCost + nextCost, resChance };
			//}
			//else if (minCostTable[nextNode].second < resChance)
			//	// 비용이 더 들긴하지만 도로포장 찬스가 더 남아있음
			//	pq.push({ {nextNode, resChance}, nowCost + nextCost });
			if (minCostTable[nextNode][resChance] > nowCost + nextCost) {
				pq.push({ {nextNode, resChance}, nowCost + nextCost });
				minCostTable[nextNode][resChance] = nowCost + nextCost;
			}

			// 다음 노드까지 도로를 포장한다.
			//if (resChance >= 1) {
			//	if (minCostTable[nextNode].first > nowCost) {
			//		pq.push({ {nextNode, resChance - 1}, nowCost });
			//		// minCost 테이블도 갱신
			//		minCostTable[nextNode] = { nowCost, resChance - 1 };
			//	}
			//	else if (minCostTable[nextNode].second < resChance - 1)
			//		// 비용이 더 들긴하지만 도로포장 찬스가 더 남아있음
			//		pq.push({ {nextNode, resChance - 1}, nowCost });
			//}
			if (resChance >= 1) {
				if (minCostTable[nextNode][resChance - 1] > nowCost) {
					pq.push({ {nextNode, resChance - 1}, nowCost });
					minCostTable[nextNode][resChance - 1] = nowCost;
				}
			}
		}
	}
}

int main() {
	cin >> N >> M >> K;

	for (int i = 0; i < M; i++) {
		int a, b, cost;
		cin >> a >> b >> cost;

		graph[a].push_back({ b, cost });
		graph[b].push_back({ a, cost });
	}

	cout << solution() << endl;
}

2022/08/31 풀이(최신)

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

typedef long long ll;

const ll MAX_COST = (ll)50000 * 1000000;

int N, M, K;
vector<vector<pair<int, int>>> graph(10000+1);

struct Node {
	int city;
	ll totalCost;
	int resChance;
};

struct cmp {
	bool operator()(const Node& n1, const Node& n2) {
		if (n1.totalCost != n2.totalCost) {
			// 오름차순
			return n1.totalCost > n2.totalCost;
		}
		else
			// 내림차순
			return n1.resChance < n2.resChance;
	}
};

ll solution() {
	priority_queue<Node, vector<Node>, cmp> pq;
	// 시작 노드
	Node nStart = { 1, 0, K };
	pq.push(nStart);

	// 최단거리 테이블
	vector<vector<ll>> minCostTable(N + 1, vector<ll>(20 + 1, MAX_COST));
	minCostTable[1][K] = 0;

	while (!pq.empty()) {
		Node nowNode = pq.top();
		pq.pop();

		int city = nowNode.city;
		ll totalCost = nowNode.totalCost;
		int resChance = nowNode.resChance;

		if (city == N)
			return totalCost;

		if (minCostTable[city][resChance] < totalCost)
			continue;

		// 주변 노드 탐색
		for (int i = 0; i < graph[city].size(); i++) {
			int nextCity = graph[city][i].first;
			ll cost = graph[city][i].second;

			if (resChance > 0) {
				if (totalCost < minCostTable[nextCity][resChance-1]) {
					Node wrappingNode = { nextCity, totalCost + 0, resChance - 1 };
					pq.push(wrappingNode);
					minCostTable[nextCity][resChance - 1] = totalCost;
				}
			}

			if (totalCost + cost < minCostTable[nextCity][resChance]) {
				Node unWrappingNode = { nextCity, totalCost + cost, resChance };
				pq.push(unWrappingNode);
				minCostTable[nextCity][resChance] = totalCost + cost;
			}
		}

	}
}

int main() {
	cin >> N >> M >> K;
	for (int i = 0; i < M; i++) {
		int a, b, c;
		cin >> a >> b >> c;
		graph[a].push_back({ b, c });
		graph[b].push_back({ a, c });
	}

	ll answer = solution();
	cout << answer << endl;
	return 0;
}