[트리(Tree)] 이진 검색 트리(Binary Search Tree)

reference: "전문가를 위한 C++" / 마크 그레고리

이진 검색 트리(BST) 속성

• 부모 노드의 값 >= 왼쪽 자식 노드의 값
• 부모 노드의 값 <= 오른쪽 자식 노드의 값

---

BST 원소 삽입 및 삭제

삽입

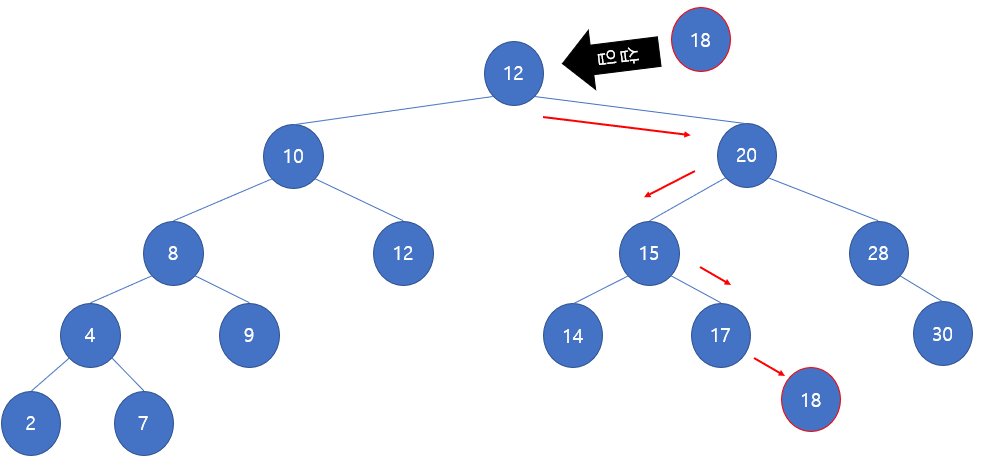
삭제

세 가지 경우를 따져야 함

1) 삭제할 노드의 자식 노드가 없는 경우: 단순히 해당 노드를 삭제함
2) "" 자식 노드가 하나만 있는 경우: 노드 삭제 후, 부모 노드의 포인터가 해당 자식 노드를 가리키도록 조정함
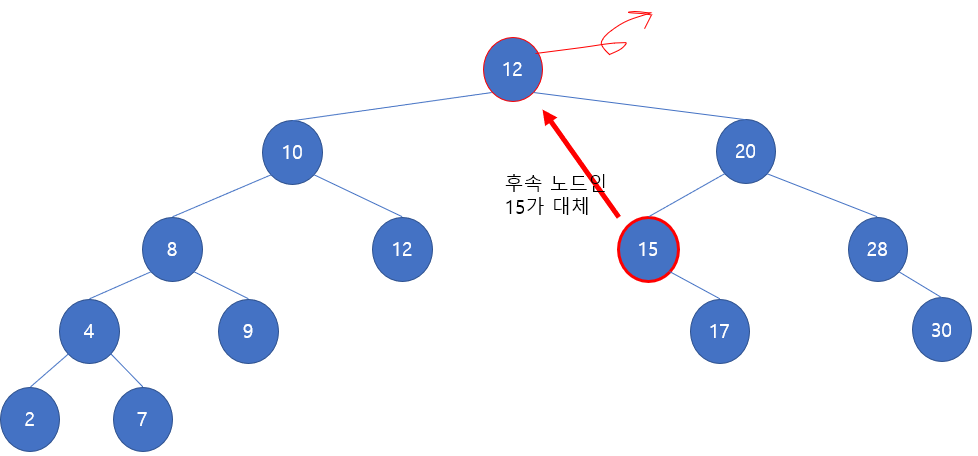
3) "" 자식 노드가 2개인 경우: 노드 삭제 후, 현재 노드를 후속 노드로 대체. 후속 노드란 현재 원소보다 큰 원소들 중 가장 작은 원소를 의미. 이 원소를 찾기 위해선 오른쪽 서브트리 중 가장 왼쪽에 있는 노드를 찾으면 됨.
(후속노드가 없다면 왼쪽 자식 노드 루트를 가리킴)

---

BST 시간 복잡도

BST에서 원소를 검색할 때는 트리의 모든 원소를 방문하지 않아도 된다. 현재 노드가 찾고자하는 노드가 아닐 때마다 검색 범위가 반으로 줄어듬.

이러한 특징은 선형 자료 구조에 대한 이진 검색에서도 유사하게 나타나며, 이는 분할 정복에서 많이 사용됨.

BST가 완전 이진 트리 형태라면 검색 및 삽입 그리고 삭제 동작의 시간 복잡도는 모두 O(logN)이고, BST가 균형 트리 형태가 아니라면 최악의 경우 O(n)(불균형 트리 또는 변질 이진 트리)이다.
=> 결국 BST의 검색 시간 복잡도는 O(트리의 높이)가 된다.

---

균형 트리: AVL 트리, Red-Black 트리

검색의 시간 복잡도를 최적화하려면 트리의 높이가 최적화 되어야 한다. 이러한 작업을 트리의 균형 잡기라 한다. 트리의 균형을 잡기 위해 트리 원소 삽입, 트리 원소 삭제 후 트리 구성을 조정해야 한다.

트리의 균형을 잡는 방법은 여러 가지가 있으며, 이를 통해 AVL 트리, 레드-블랙 트리 같은 다양한 트리를 만들 수 있다. AVL 트리의 기본 아이디어는 BST 속성을 유지하면서 트리 높이의 균형을 잡기 위해 약간의 회전을 수행하는 것이다.

---

BST 구현하기

#include <iostream>
using namespace std;

// 노드 구조체
struct node {
	int data;
	node* left;
	node* right;
};

// bst 구조체
struct bst {
	node* root = NULL;
	

// 검색 함수 => O(logN), 최악의 경우 O(n)
	node* find(int value) {
		// find_impl의 래퍼
		return find_impl(root, value);
	}
private:
	// private으로 외부에서 직접 호출할 수 없도록
	node* find_impl(node* current, int value) {
		if (!current) {
			cout << endl;
			return NULL;
		}

		if (current->data == value) {
			cout << value << " 발견" << endl;
			return current;
		}

		if (value < current->data) {
			cout << current->data << "에서 왼쪽으로 이동" << endl;
			return find_impl(current->left, value);
		}
		else {
			cout << current->data << "에서 오른쪽으로 이동" << endl;
			return find_impl(current->right, value);
		}
	}


// 삽입 함수 => O(logN), 최악의 경우 O(n)
public:
	void insert(int value) {
		if (!root)
			root = new node{ value, NULL, NULL };
		else
			insert_impl(root, value);
	}
private:
	void insert_impl(node* current, int value) {
		if (value < current->data) {
			if (!current->left)
				current->left = new node{ value, NULL, NULL };
			else
				insert_impl(current->left, value);
		}
		else {	// (value > current-> data)
			if (!current->right) {
				if (!current->right)
					current->right = new node{ value, NULL, NULL };
				else
					insert_impl(current->right, value);
			}
		}
	}




// 삭제 함수 => O(logN), 최악의 경우 O(n)
public:
	void deleteValue(int value) {
		root = delete_impl(root, value);
	}
private:
	// 후속 노드 찾기
	// 후속 노드: 현재 노드 다음으로 큰 숫자, 즉 현재 원소보다 큰 원소들 중에서 가장 작은 원소를 의미.
	// 현재 노드의 오른쪽 서브 트리로 이동 후 서브 트리에서 가장 왼쪽에 위치한 노드로 이동. 
	node* successor(node* start) {
		auto current = start->right;
		while (current && current->left)
			current = current->left;
		return current;
	}

	node* delete_impl(node* start, int value) {
		if (!start)
			return NULL;

		// 왼쪽이동
		if (value < start->data) {
			start->left = delete_impl(start->left, value);
		}
		// 오른쪽이동
		else if (value > start->data) {
			start->right = delete_impl(start->right, value);
		}
		// 발견
		else {
			// 자식이 없거나, 왼쪽 자식만 없는 경우
			if (!start->left) {
				auto temp = start->right;
				delete start;
				return temp;
			}
			// 오른쪽 자식만 없는 경우
			if (!start->right) {
				auto temp = start->left;
				delete start;
				return temp;
			}

			// 자식이 둘 다 있는 경우
			auto sucNode = successor(start);
			start->data = sucNode->data;
			
			// 오른쪽 서브트리에서 sucNode 삭제
			start->right = delete_impl(start->right, sucNode->data);
		}

		return start;
	}
};