이전 포스팅에서 불균형 트리, 균형 트리에 대해 언급한 적이 있다. 본 포스팅은 트리의 종류에 대해 좀더 자세히 알고 추후 자료구조 공부에 활용하고자 한다.
그림 source: https://towardsdatascience.com/5-types-of-binary-tree-with-cool-illustrations-9b335c430254
Full binary tree (정 이진 트리)
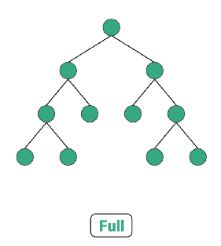
- 트리의 각 노드는 자식 노드를 하나도 가지지 않거나 두 개를 가져야 한다는 조건이 있다.
- 즉, 자식 노드 갯수가 0 또는 2 이므로 홀수 개의 자식 노드를 가질 수 없다.
Complete binary tree (완전 이진 트리)

- 부모 -> 왼쪽 자식 -> 오른쪽 자식 순으로 채워지는 트리이다.
- 마지막 레벨을 제외하면, 모든 레벨에 노드들이 차 있다는 특징을 지닌다.
- 마지막 레벨의 경우 노드들이 왼쪽에서부터 차 있다는 특징을 지닌다.
- 완전 이진 트리는 배열 자료구조로 담아내기 좋다.
- 배열을 이용하여 저장하면, 다른 노드를 가리키는 포인터를 저장할 필요가 없기에 메모리 사용 측면에서 효율적이다.
- 완전 이진 트리 형태의 탐색 트리에서는 검색에 대한 시간 복잡도가 O(logN)임을 거의 보장한다.
- 반면 삽입/삭제에선 O(logN)을 보장할 수 없다. 단순히 이진 탐색 트리 성질에 완전 이진 트리 구조까지 맞추어야 하기 때문이다.
- 탐색이 많은 경우 유리하고, 삽입 및 삭제 빈도수가 높아지면 높아질 수록 효율성이 떨어진다.
- 이러한 불편함을 해결한 것이 균형 트리의 일종인 AVL 트리가 있다.
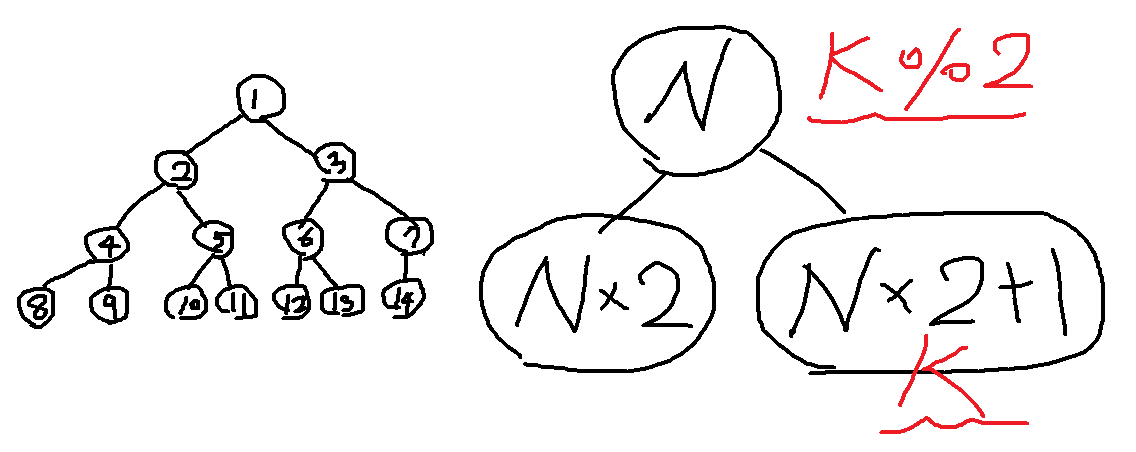

source: https://debugdaldal.tistory.com/25
Perfect binary tree (포화 이진 트리)

- 정 이진 트리 + 완전 이진 트리
- 모든 리프 노드의 레벨이 동일하고, 모든 레벨에 노드들이 차 있다는 특징을 지닌다.
Balanced binary tree (균형 이진 트리)
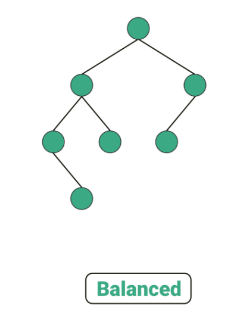
- 정 이진 트리처럼 자식 노드 갯수에 대한 제약이 있거나, 완전 이진 트리처럼 마지막 레벨에서는 왼쪽에서 오른쪽 방향으로 노드가 추가되어야 한다는 제약이 있는 것은 아니지만,
트리가 한쪽으로 치우치는 불균형 트리와 같은 구조가 아닌 균형이 잡힌 트리이다. - 오른쪽 서브트리의 높이와 왼쪽 서브트리의 높이 차이가 1 이하가 되어야 한다.
- 완전 이진 트리 형태의 탐색 트리와 마찬가지로 균형 이진 트리 형태의 탐색 트리에서 탐색/삽입/검색에 대한 시간 복잡도가 O(logN)임을 거의 보장한다.
- 균형이 깨지는 경우 여러 가지 회전 연산을 통해 트리의 균형을 잡는다.
Degenerate binary tree (변질 이진 트리 또는 불균형 트리)
- 각 부모 노드가 오직 한 개의 자식 노드를 갖는 트리 형태가 되어 사실상 연결 리스트와 별반 다를게 없게 된 트리이다.
- 트리 연산에 대한 시간 복잡도가 O(N)이 된다.
