[조합] 부분수열의 합 vs 부분수열의 합2

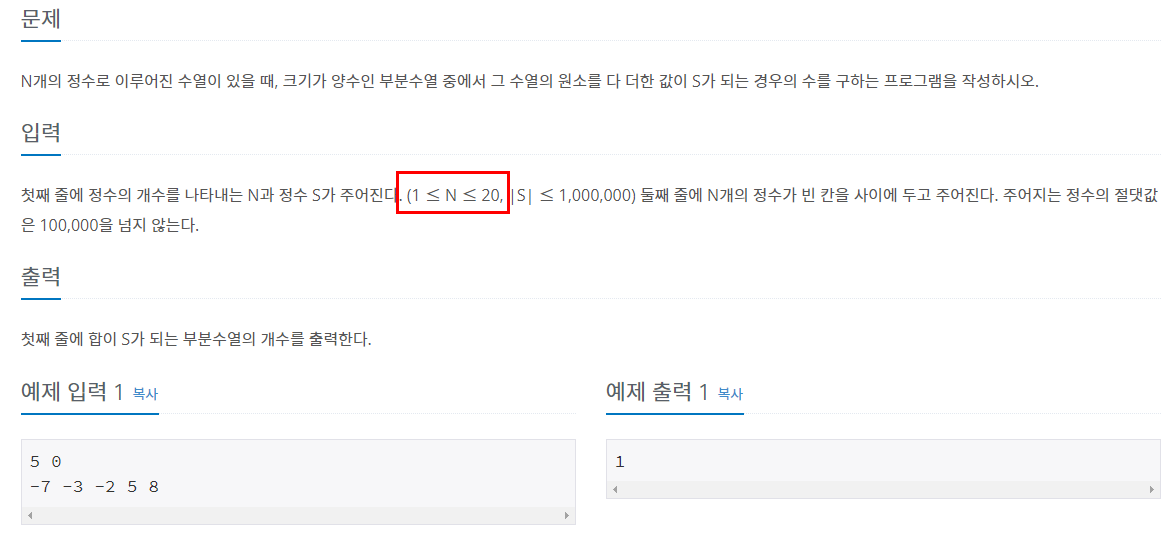
부분수열의 합(1182번)_백준

source: https://www.acmicpc.net/problem/1182

시간 복잡도: O(2^n)
N은 최대 20이므로 최대 시간 복잡도는 O(2^20) = O(1,048,576)이다.

#include <iostream>
#include <vector>
using namespace std;

int N, S;

void findCombination(const vector<int>& nums, int startIdx, int sum, int& cnt) {
	// 종료조건
	if (startIdx >= N)
		return;

	// 탐색
	for (int i = startIdx; i < N; i++) {
		int num = nums[i];
		if (sum + num == S)
        	// S와 같은 합을 발견하면 참조 변수를 갱신
			cnt += 1;
		
		findCombination(nums, i + 1, sum + num, cnt);
	}

}

int solution(const vector<int>& nums) {

	int cntOfCombination = 0;	// 최종 답을 담을 변수를 참조로 넘긴다. 
	findCombination(nums, 0, 0, cntOfCombination);
	return cntOfCombination;
}

int main() {
	cin >> N >> S;

	vector<int> nums(N);
	for (int i = 0; i < N; i++) {
		cin >> nums[i];
	}

	int answer = solution(nums);
	cout << answer << '\n';
}

---

부분수열의 합2(1182번)_백준

source: https://www.acmicpc.net/problem/1208

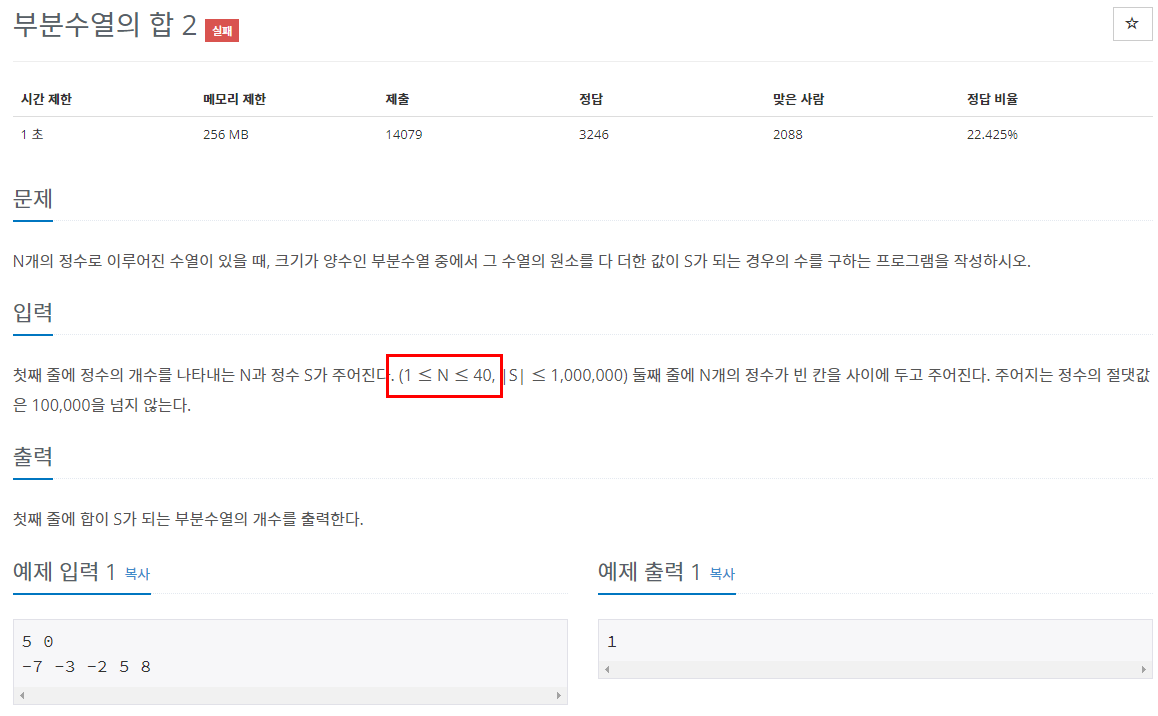
이 문제는 위 코드로는 시간초과가 뜬다.
N의 범위가 40가지 이므로 O(2^40) = O(1,099,511,627,776)이 된다. 당연히 시간 초과가 뜬다.

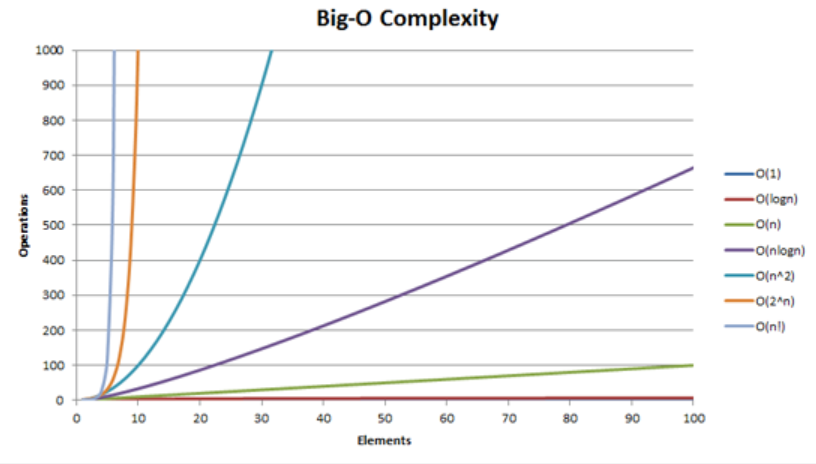
모든 조합의 시간복잡도는 2^n, 지수적 증가이므로 n이 클수록 폭발적으로 증가한다.

부분수열의 합2를 단순 조합으로 풀면 안된다!

• 연속된 수열을 찾는다 하면 경우의 수가 크지 않겠지만 연속된 수열이라는 말이 언급되지 않았기 때문에 부분집합을 고려해야한다.

• 부분집합의 최대갯수는 2^N 즉 최대 2^40까지 가능하다. => 시간초과

• 해결방법으로는 N을 2로 나눈 후 두 경우로 나누어 해결해야한다.

1. 조합의 합의 범위는 최소 -4,000,000에서 최대 4,000,000이다. 조합들을 계산하여 나올 수 있는 합의 경우의 수를 카운트하기 위한 벡터를 선언한다.

// -40*100,000 ~ -1
vector<int> minusCnt(40 * 100000 + 1, 0);
// minusCnt[1]은 합이 '-1'이 되는 조합의 경우의 수를 의미
// minusCnt[4000000]은 합이 '-4,000,000'이 되는 조합의 경우의 수를 의미

// 0 ~ 40*100,000
vector<int> plusCnt(40 * 100000 + 1, 0);
// plusCnt[0]은 합이 '0'이 되는 조합의 수를 의미
// plusCnt[4000000]은 합이 '4,000,000'이 되는 조합의 수를 의미 

2. 먼저 N/2개의 왼쪽 원소들의 조합 케이스를 구한다. 이렇게 함으로써 최대 시간 복잡도는 O(2^40)에서 O(2^20)으로 줄어든다.

void findCombination_left(const vector<int>& nums, int startIdx, int sum, vector<int>& minusCnt, vector<int>& plusCnt) {
	// 탐색						// N/2
	for (int i = startIdx; i < nums.size(); i++) {
		int num = nums[i];
		if (sum + num < 0) {
			minusCnt[-(sum + num)]++;
		}
		else {
			plusCnt[sum + num]++;
		}

		findCombination_left(nums, i + 1, sum + num, minusCnt, plusCnt);
	}
}

3. 왼쪽 부분의 조합 중 정답이 되는 케이스를 구한다.

// solution 함수
    // 왼쪽 2^20개에 대한 조합 구하기
	findCombination_left(leftNums, 0, 0, minusCnt, plusCnt);
	if (S < 0) {
		answer += minusCnt[-S];
	}
	else {
		answer += plusCnt[S];
	}

4. N/2개의 오른쪽 원소들의 조합 케이스를 구하면서 정답 조건이 되는 합을 카운트한다.

void findCombination_right(ll& answer, const vector<int>& nums, int startIdx, int sum, const vector<int>& minusCnt, const vector<int>& plusCnt) {
	// 탐색
	for (int i = startIdx; i < nums.size(); i++) {
		int num = nums[i];
		if (num + sum == S)
			answer++;
		if (S - (sum + num) < 0) {
			//S - (sum + num) = leftSum;
			answer += minusCnt[-(S - (sum + num))];
		}
		else {
			answer += plusCnt[S - (sum + num)];
		}

		findCombination_right(answer, nums, i + 1, sum + num, minusCnt, plusCnt);
	}
}

위와 같은 방식으로 시간 복잡도를 대폭 줄이면서 문제를 해결할 수 있다.