[조합+이진탐색] 냅색문제_백준

냅색문제_백준

source: https://www.acmicpc.net/problem/1450

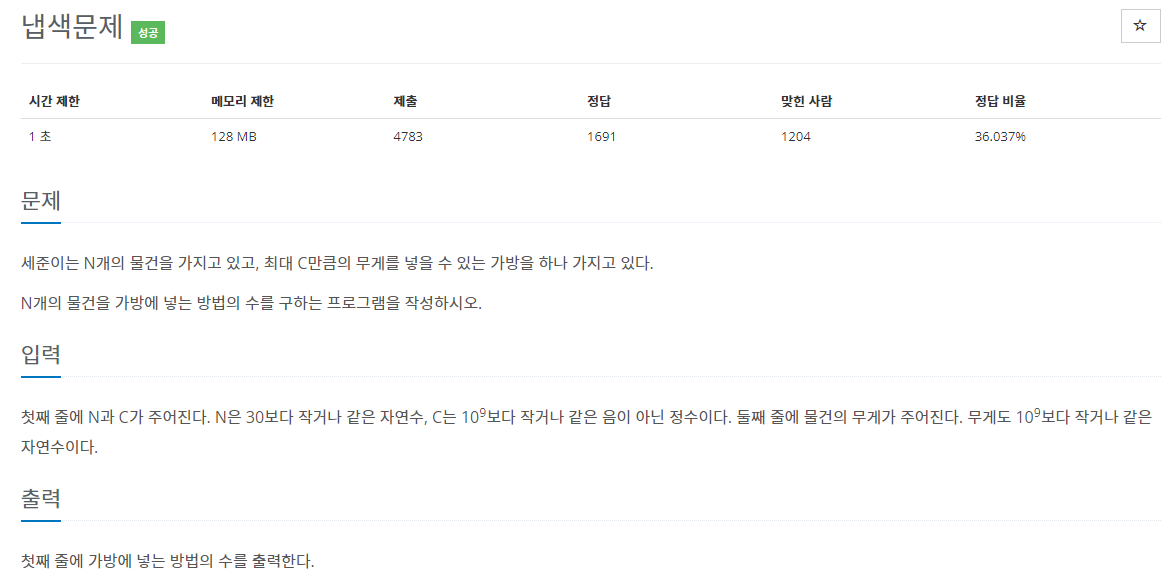
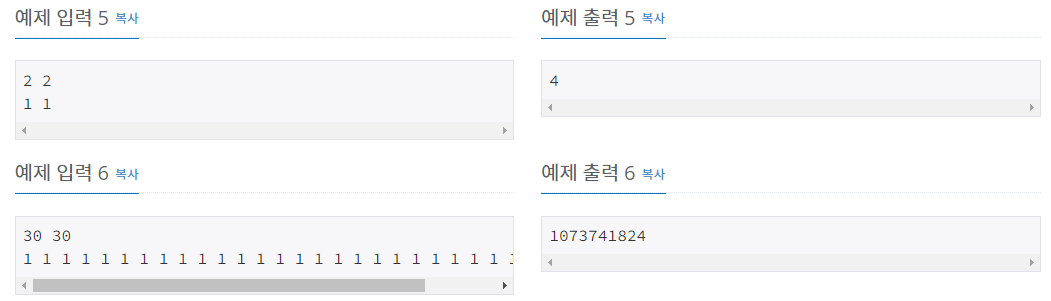
전체 조합의 케이스를 줄이는 방식이 '부분 수열2_백준' 문제와 유사하다.

reference: https://velog.io/@jinh2352/%EC%A1%B0%ED%95%A9%EC%9D%98-%EC%8B%9C%EA%B0%84%EB%B3%B5%EC%9E%A1%EB%8F%84-%EB%B6%80%EB%B6%84%EC%88%98%EC%97%B4%EC%9D%98-%ED%95%A9-vs-%EB%B6%80%EB%B6%84%EC%88%98%EC%97%B4%EC%9D%98-%ED%95%A92

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int N;
int C;

// 왼쪽 부분합
vector<int> leftPartSum;
// 오른쪽 부분합
vector<int> rightPartSum;

void left_combination(const vector<int>& vec, int startIdx, int endIdx, int sum) {
	
	// 탐색
	for (int i = startIdx; i <= endIdx; i++) {
		if (sum + vec[i] > C)
			continue;

		leftPartSum.push_back(sum + vec[i]);
		left_combination(vec, i + 1, endIdx, sum + vec[i]);
	}
}

void right_combination(const vector<int>& vec, int startIdx, int endIdx, int sum) {

	// 탐색
	for (int i = startIdx; i <= endIdx; i++) {
		if (sum + vec[i] > C)
			continue;

		rightPartSum.push_back(sum + vec[i]);
		right_combination(vec, i + 1, endIdx, sum + vec[i]);
	}
}

int findSmallerThanCnum(const vector<int>& partSum, int C) {
	int start = 0;
	int end = partSum.size() - 1;

	int maxIdx = -1;
	while (start <= end) {
		int mid = (start + end) / 2;

		if (partSum[mid] <= C) {
			// 최대 인덱스를 저장하고, 탐색 범위를 늘려본다.
			maxIdx = max(maxIdx, mid);
			start = mid + 1;
		}
		else {	// C < partSum[mid] 
			// => 탐색 범위를 줄인다.
			end = mid - 1;
		}
	}

	return maxIdx + 1;	// C보다 큰 갯수
}

int solution(const vector<int>& vec) {
	// 왼쪽 부분합 case 구하기: 시간 복잡도 최대 O(2^15)로 축소
	left_combination(vec, 0, N / 2, 0);

	// 오른쪽 부분합 case 구하기: 시간 복잡도 최대 O(2^15)로 축소
	right_combination(vec, N / 2 + 1, N-1, 0);

	// 경우의 수 구하기
	int totalSum = 1;	// 아무것도 넣지 않은 경우
	// 정렬: O(nlogn)		// n은 약 40,000
	sort(leftPartSum.begin(), leftPartSum.end());
	sort(rightPartSum.begin(), rightPartSum.end());
	// 왼쪽 partSum에서 C보다 작은 원소 갯수 구하기	// => 정렬 후 이진탐색(인덱스를 바탕으로 갯수 판단)
	totalSum += findSmallerThanCnum(leftPartSum, C);
	// 오른쪽 partSum에서 C보다 작은 원소 갯수 구하기 // => 정렬 후 이진탐색(인덱스를 바탕으로 갯수 판단)
	totalSum += findSmallerThanCnum(rightPartSum, C);

	// 왼쪽/오른쪽 partSum 조합으로 C보다 작은 경우의 수 구하기
	for (int i = 0; i < leftPartSum.size(); i++) {
		if (leftPartSum[i] > C)
			break;

		int lsum = leftPartSum[i];
		// 이진탐색
		totalSum += findSmallerThanCnum(rightPartSum, C - lsum);
	}

	return totalSum;
}

int main() {
	cin >> N >> C;
	vector<int> vec(N);
	for (int i = 0; i < N; i++) {
		cin >> vec[i];
	}

	int answer = solution(vec);
	cout << answer << '\n';

	return 0;
}