[최대공약수와 최소공배수(with 유클리드)] 템플릿 코드와 예제 문제: 멀쩡한 사각형_프로그래머스

최대 공약수(GCD), 최소 공배수(LCM)

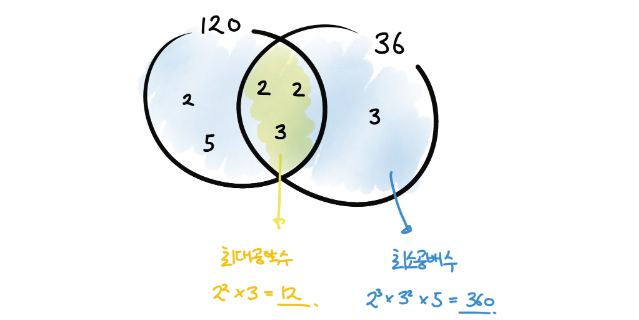
source: https://dimenchoi.tistory.com/46

최대공약수

int gcd(int a, int b){
    // a가 크다고 가정한다.
    if(a < b){
    	int temp = b;
        b = a;
        a = temp;
    }
    
    while(b != 0){	// b가 0이 아닐 때 까지 반복
    	int temp = a % b;
        a = b;
        b = temp;
    }
    
    // 반복문을 벗어나 더 큰 값인 a를 반환
    return a; 
}

최소공배수

int lcm(int a, int b){
	// a가 크다고 가정한다.
    if(a < b){
    	int temp = b;
        b = a;
        a = temp;
    }
    
    return a * b / gcd(a, b);	// a*b / 최대공약수

---

예제 문제: 멀쩡한 사각형_프로그래머스

https://programmers.co.kr/learn/courses/30/lessons/62048?language=cpp#

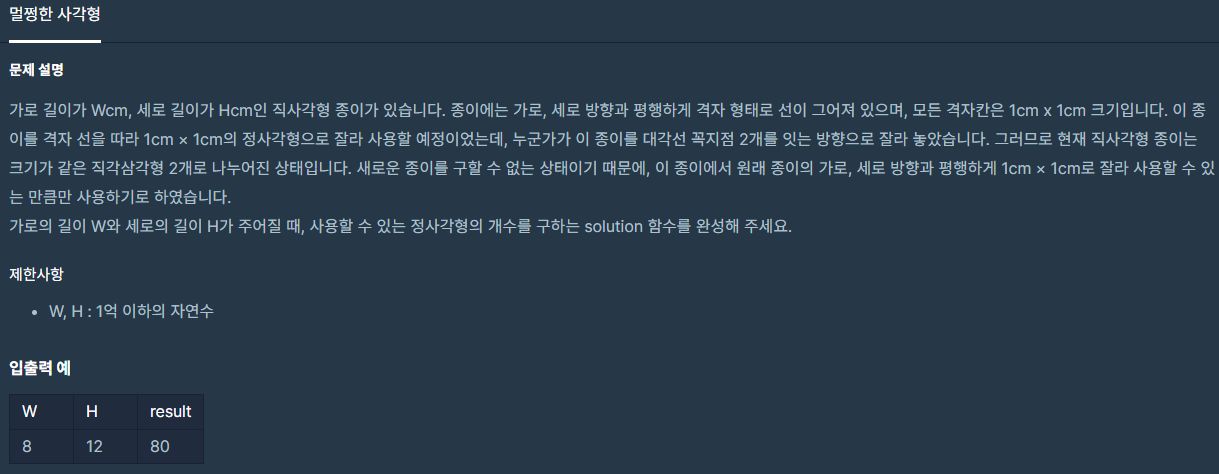
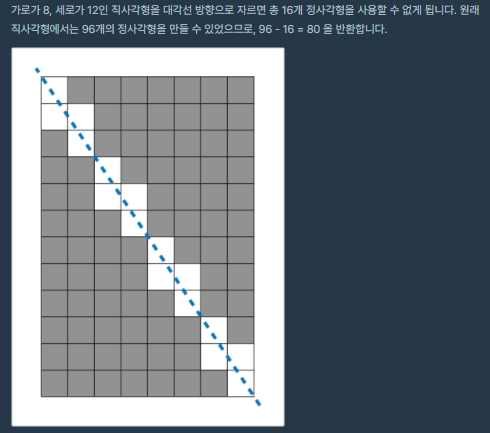
이 문제는 최대공약수를 적절히 이용했어야 했다. 최대공약수를 사용하지 않아도 풀리긴 하였지만 소수 오차에 의해 단 한개의 테케가 계속 틀리는 현상이 발생하였다.

---

먼저 기존 풀이법이다. 공약수를 사용하지 않고 모든 w를 계산하며 하나의 열에서 제외해야 할 블럭의 수를 계산해나가는 방식이다.
이 풀이의 문제점은 수의 범위와 관련이 있다. 문제 조건에서 제한사항이 w와 h는 1억 이하의 자연수이다. 생각보다 큰 수이다. 따라서 기울기와 곱하는 과정에서 아무리 기울기가 double이라지만 원하지 않은 값을 받을 수 있다는 것이다.

long long solution(int w,int h) {

    // 먼저 모든 정사각형을 구한다. 
    long long answer = (long long)w * (long long)h;
       
    // (1) 정사각형일때
    if(w==h){
        answer -= w;
        return answer;   
    }
    
    // (2) 정사각형이 아닌 직사각형일 때 
    // 기울기
    double giulgi = ((double)h/(double)w);  // 기울기
    long long total = 0;
    for(int i=0; i<w; i++){
        long long a = giulgi*i;   // 내림 또는 정수
        long long b;
       
        if(giulgi*(i+1) == (int)(giulgi*(i+1))){
            b = giulgi*(i+1);   // 정수
        }
        else{   // 올림
            b = (long long)(giulgi*(i+1)) + (long long)1;
        }
        
        // 하나의 행 또는 열에서 제외해야할 블럭 수: b-a; 
        total += (b-a);
    }
        
    return answer - total;
}

따라서 공약수를 구해서 크기를 축소시킨다. 그리고 이 안에서 구할 수 없는 블록의 수를 센 후 배수를 다시 곱해주면 된다. 이를 통해 계산의 오차를 줄이는 것이다.

int gcd(int a, int b) { // 최대공약수 함수 (반복문 버전)
    // a가 더 크다고 가정
    
    int temp;
    while(b!=0){    // b가 0이 아닐때까지 반복
        temp = a % b;
        a = b;
        b = temp;
    }
    
    return a;
    
    
}

long long solution(int w,int h) {
    long long answer = (long long)w * (long long)h;
    
    
    // (1) 정사각형일때 (특수 케이스)
    if(w==h){
        answer -= w;
        return answer;   
    }

    // 최대공약수 구하기
    int limit;	// limit 만큼 축소시킨다.
    int gob;	// 나중에 곱해줄 배수를 구한다. 
    double giulgi;	// 기울기 
    if(w > h){
        limit = w/gcd(w, h);    // w / 최대 공약수
        giulgi = ((double)h/(double)w);
        gob = gcd(w, h); 
    }
    else{
        limit = h/gcd(h, w);
        giulgi = ((double)w/(double)h);
        gob = gcd(h, w);
    }
    
    
    // 기울기
    //double giulgi = ((double)h/(double)w);  // 기울기
    long long total = 0;
    for(int i=0; i<limit; i++){	   // 범위를 축소시켜 소수 계산의 오차를 줄이자!
        long long a = giulgi*i;   // 내림 또는 정수
        long long b;
        
        //float b = gigulgi*(i+1);    
        if(giulgi*(i+1) == (int)(giulgi*(i+1))){
            b = giulgi*(i+1);   // 정수
        }
        else{   // 올림
            b = (long long)(giulgi*(i+1)) + (long long)1;
        }
        
        // 블록 수 세기
        total += (b-a);
    }

    total *= gob;	// 배수를 곱함
        
    return answer - total;
}