힙의 시간 복잡도
우선순위 큐의 내부 구조는 힙이다. 힙은 아래와 같은 연산에 대한 시간 복잡도를 만족해야 한다.
-
최대/최소 원소 접근(pq.top()): O(1)
-
원소 삽입에 대한 시간 복잡도(pq.push(..)): O(logN)
-
최대 원소 삭제에 대한 시간 복잡도(pq.pop()): O(logN)
힙의 기반 자료구조
위와 같이 힙은 원소 삽입/삭제에 대해 O(logN)의 시간 복잡도를 만족하기 위해 이진 트리 구조를 사용하고, 특히 완전 이진 트리를 사용한다.
이진 탐색 트리의 성질과 일치하지 않는다. 부모 노드의 왼쪽 자식에는 부모 노드의 값보다 작은 값, 오른쪽 자식에는 부모 노드 값보다 큰 값이 반드시 설정될 필요는 없다.
힙의 불변성
원소를 삽입하거나 삭제할 때 유지해야할 힙의 불변성이 있다.
최대(또는 최소) 원소에 즉각적으로 접근 가능해야 한다.
=> 최대('') 원소가 항상 고정된 위치에 있어야 한다.
=> 부모 노드가 두 자식 노드보다 항상 커야한다.
이진 검색 트리에 비해 조건이 간소화됨을 알 수 있다. 이진 조건 트리에서 루트 노드부터 점차적으로 큰 값을 계속하여 삽입할 경우 불균형 트리가 만들어질 수 있는데 힙은 그렇지 않다. 항상 완전 이진 트리가 유지된다.
완전 이진 트리는 노드 개수를 알면 트리의 구조를 확정할 수 있다.
힙 종류
-
최대 힙(max heap)
: 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리 -
최소 힙(min heap)
: 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진 트리
힙 구현
힙은 완전 이진 트리이므로 배열로 구현할 수 있다.
(루트 노드의 번호가 0이라 가정)
- i번 노드의 왼쪽 자식은 2xi+1번
- i번 노드의 오른쪽 자식은 2xi+2번
- i번 노드의 부모는 (i-1)/2번
- 원소의 삽입
- 새로운 원소를 배열의 가장 끝에 삽입하여 부모 노드와 비교하고 swap하며 상위 레벨로 나아간다.
- 원소의 삭제
- 루트 노드와 배열 맨 끝 노드를 swap하는 동시에 기존의 루트 노드를 제거한다. 그리고 두 자식 노드와 비교하며 값이 더 큰 노드(자식끼리도 크면서, 자신보다도 더 큰)와 swap하며 하위 레벨로 내려간다.
1. 힙에 원소 삽입
다음 (1), (2)를 모두 만족하는 과정으로 삽입이 이루어져야 한다.
(1) 힙에 새 원소를 삽입하려면 단순히 배열의 맨 마지막 위치에 원소를 추가하면 된다.
(2) 모든 노드는 자식 노드보다 더 큰 값을 가지고 있어야 한다.
=> 새 원소를 맨 마지막 노드로 삽입하고, 부모 노드와 값 비교를 하면서 스왑(swap)해 나간다.
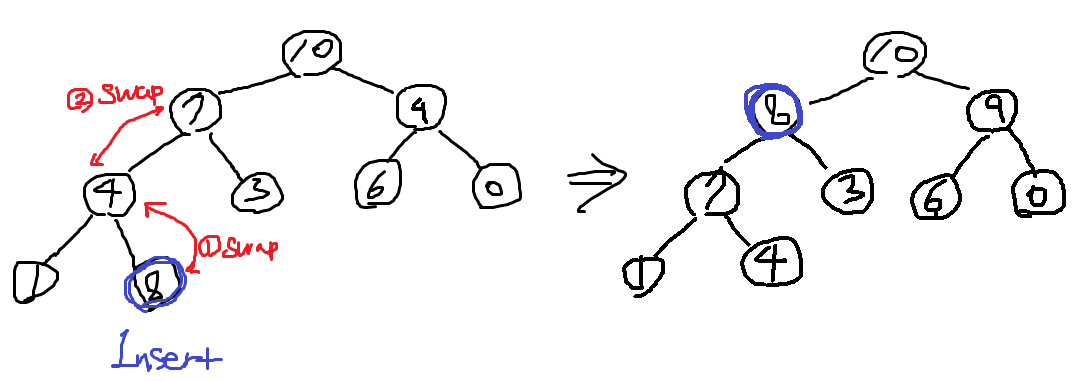
=> 시간 복잡도: O(logN)
2. 힙에서 원소 삭제
(1) 완전 이진 트리에서 하나의 노드를 삭제하면 그 구조는 유지한 채 마지막 노드가 하나 빠져나가듯 해야 한다.
(2) 힙에서는 가장 큰 원소(또는 가장 작은 원소)만 삭제할 수 있다.
=> 루트 노드와 트리의 맨 마지막 노드를 서로 교환한 후, 마지막 노드를 삭제한다. 그리고 루트 노드와 자식 노드를 교체해 나가며 루트 노드가 아래로 제자리를 찾게 한다.
이를 통해 최대(또는 최소) 원소 삭제와 부모 노드가 자식 노드보다 커야한다는 불변성을 만족시킬 수 있다.

=> 시간 복잡도: O(logN)
3. 힙 초기화
벡터, 리스트와 달리 힙은 불변성을 유지해야 하기에 초기화가 간단하지 않다.
가장 간단한 방법으로는 비어있는 힙에 초기 원소들을 하나씩 삽입하는 것이다. 하지만 이 방식의 전체 시간 복잡도는 O(NlogN)이다.
하지만 O(N)의 시간 복잡도로 힙을 초기화하는 알고리즘이 존재한다. 실제로 C++ 표준의 배열 또는 벡터의 반복자를 인자로 받아 힙을 구성하는 std::make_heap() 함수를 제공하고, 이 함수의 시간 복잡도는 O(N)이다.
