[백준] BOJ_11053 LIS JAVA

BOJ_11053 가장 긴 증가하는 부분 수열(LIS)

문제

수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오.

예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이고, 길이는 4이다.

---

입력

첫째 줄에 수열 A의 크기 N (1 ≤ N ≤ 1,000)이 주어진다.

둘째 줄에는 수열 A를 이루고 있는 Ai가 주어진다. (1 ≤ Ai ≤ 1,000)

---

출력

첫째 줄에 수열 A의 가장 긴 증가하는 부분 수열의 길이를 출력한다.

---

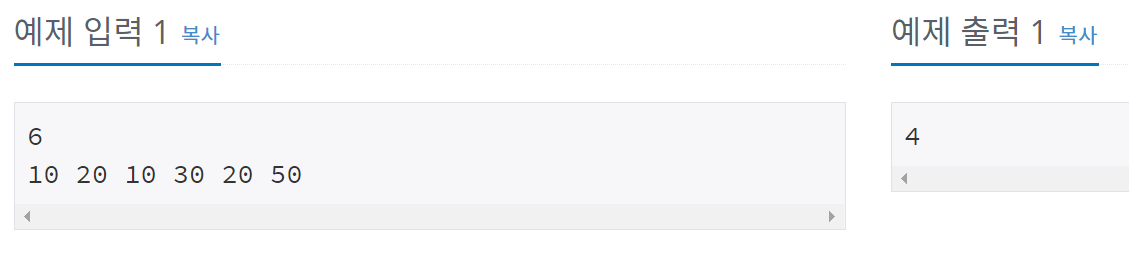
예제 입&출력

---

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int n = Integer.parseInt(br.readLine());

        int[] arr = new int[n + 1];
        int[] dp = new int[n + 1];

        StringTokenizer st = new StringTokenizer(br.readLine());

        for (int i = 1; i <= n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }
        dp[0] = 0;
        dp[1] = 1;

        for (int i = 2; i <= n; i++) {
            dp[i] = 1;
            for (int j = 1; j < i; j++) {
                if (arr[j] < arr[i] && dp[i] < dp[j] + 1) {
                    dp[i] = dp[j] + 1;
                }
            }
        }

        int answer = 0;
        for (int i : dp) {
            //System.out.print(i + " ");
            answer = Math.max(answer, i);
        }

        System.out.println(answer);
    }
}

---

Comment

• BOJ_11054 가장 긴 바이토닉 부분 수열 : LIS가 있다면? LDS도 있다. 이를 합쳐 풀어보자. 단 두 수열을 이루는 배열을 더했을 때, 공통되는 요소가 있지 않을까? (= -1을 빼먹지 말고 풀자잉~)
• 범위가 1 ≤ N ≤ 1,000이기 때문에 가능한 풀이였다. 이분탐색을 공부하고 나서 풀어볼 문제(Click!) 범위(1 ≤ N ≤ 1,000,000)

---