[백준] BOJ_11404 플로이드(플로이드 와샬) JAVA

BOJ_11404 플로이드

문제

n(2 ≤ n ≤ 100)개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 m(1 ≤ m ≤ 100,000)개의 버스가 있다. 각 버스는 한 번 사용할 때 필요한 비용이 있다.

모든 도시의 쌍 (A, B)에 대해서 도시 A에서 B로 가는데 필요한 비용의 최솟값을 구하는 프로그램을 작성하시오.

---

입력

첫째 줄에 도시의 개수 n이 주어지고 둘째 줄에는 버스의 개수 m이 주어진다. 그리고 셋째 줄부터 m+2줄까지 다음과 같은 버스의 정보가 주어진다. 먼저 처음에는 그 버스의 출발 도시의 번호가 주어진다. 버스의 정보는 버스의 시작 도시 a, 도착 도시 b, 한 번 타는데 필요한 비용 c로 이루어져 있다. 시작 도시와 도착 도시가 같은 경우는 없다. 비용은 100,000보다 작거나 같은 자연수이다.

시작 도시와 도착 도시를 연결하는 노선은 하나가 아닐 수 있다.

---

출력

n개의 줄을 출력해야 한다. i번째 줄에 출력하는 j번째 숫자는 도시 i에서 j로 가는데 필요한 최소 비용이다. 만약, i에서 j로 갈 수 없는 경우에는 그 자리에 0을 출력한다.

---

예제 입&출력

---

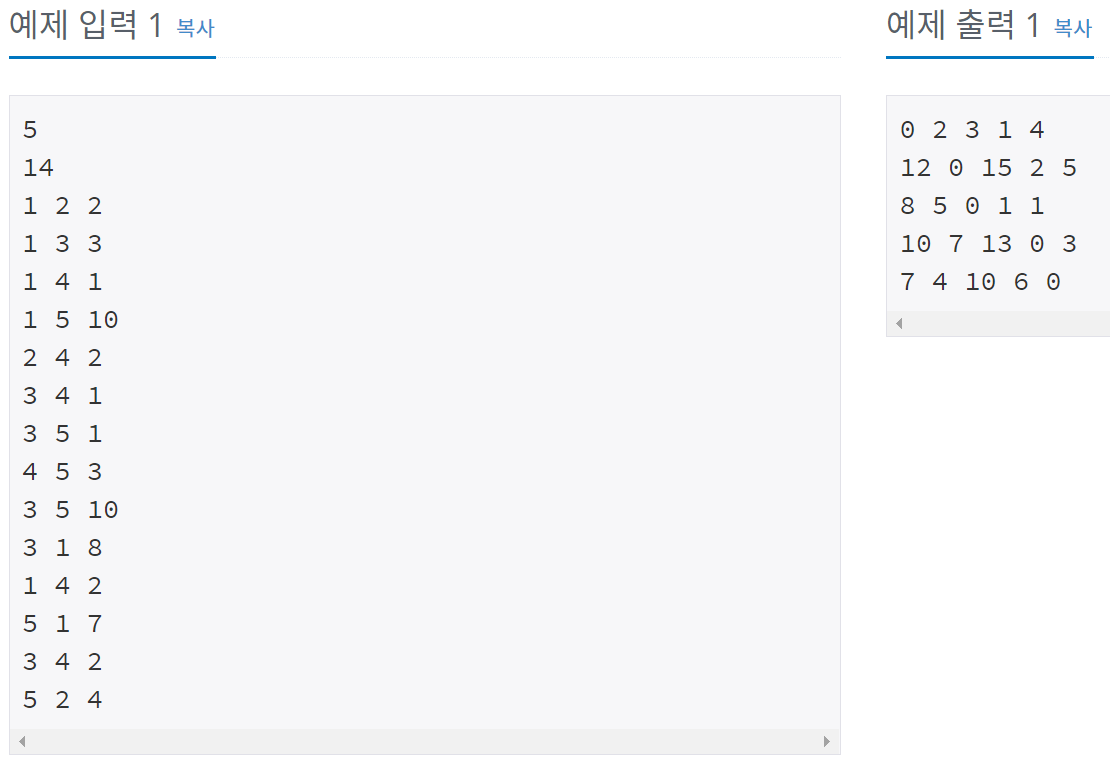
소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    private static int n, m;
    private static final int INF = 1_000_001;
    private static int[][] dist;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;

        n = Integer.parseInt(br.readLine());
        m = Integer.parseInt(br.readLine());

        dist = new int[n + 1][n + 1];

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (i == j) continue;
                dist[i][j] = INF;
            }
        }

        for (int line = 0; line < m; line++) {
            st = new StringTokenizer(br.readLine());
            int start = Integer.parseInt(st.nextToken());
            int end = Integer.parseInt(st.nextToken());
            int cost = Integer.parseInt(st.nextToken());

            dist[start][end] = Math.min(dist[start][end], cost);
        }

        floydWarshall();

        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                if (dist[i][j] == INF) System.out.print(0);
                else {
                    System.out.print(dist[i][j] + " ");
                }
            }
            System.out.println();
        }
    }

    private static void floydWarshall() {
        for (int path = 1; path <= n; path++) // path : 거쳐가는 정점
            for (int i = 1; i <= n; i++) { // i : 시작 정점
                for (int j = 1; j <= n; j++) { // j : 끝 정점
                    dist[i][j] = Math.min(dist[i][j], dist[i][path] + dist[path][j]);
                }
            }
    }
}

---

Comment

• 다익스트라 알고리즘 : 한 정점으로 부터 모든 정점에 이르는 간선 정보(BFS)
• 플로이드-와셜 알고리즘 : 모든 정점으로 부터 모든 정점에 이르는 간선 정보(DP)

---