[백준] BOJ_11657 타임머신(벨만-포드) JAVA

BOJ_11657 타임머신

문제

N개의 도시가 있다. 그리고 한 도시에서 출발하여 다른 도시에 도착하는 버스가 M개 있다. 각 버스는 A, B, C로 나타낼 수 있는데, A는 시작도시, B는 도착도시, C는 버스를 타고 이동하는데 걸리는 시간이다. 시간 C가 양수가 아닌 경우가 있다. C = 0인 경우는 순간 이동을 하는 경우, C < 0인 경우는 타임머신으로 시간을 되돌아가는 경우이다.

1번 도시에서 출발해서 나머지 도시로 가는 가장 빠른 시간을 구하는 프로그램을 작성하시오.

---

입력

첫째 줄에 도시의 개수 N (1 ≤ N ≤ 500), 버스 노선의 개수 M (1 ≤ M ≤ 6,000)이 주어진다. 둘째 줄부터 M개의 줄에는 버스 노선의 정보 A, B, C (1 ≤ A, B ≤ N, -10,000 ≤ C ≤ 10,000)가 주어진다.

---

출력

만약 1번 도시에서 출발해 어떤 도시로 가는 과정에서 시간을 무한히 오래 전으로 되돌릴 수 있다면 첫째 줄에 -1을 출력한다. 그렇지 않다면 N-1개 줄에 걸쳐 각 줄에 1번 도시에서 출발해 2번 도시, 3번 도시, ..., N번 도시로 가는 가장 빠른 시간을 순서대로 출력한다. 만약 해당 도시로 가는 경로가 없다면 대신 -1을 출력한다.

---

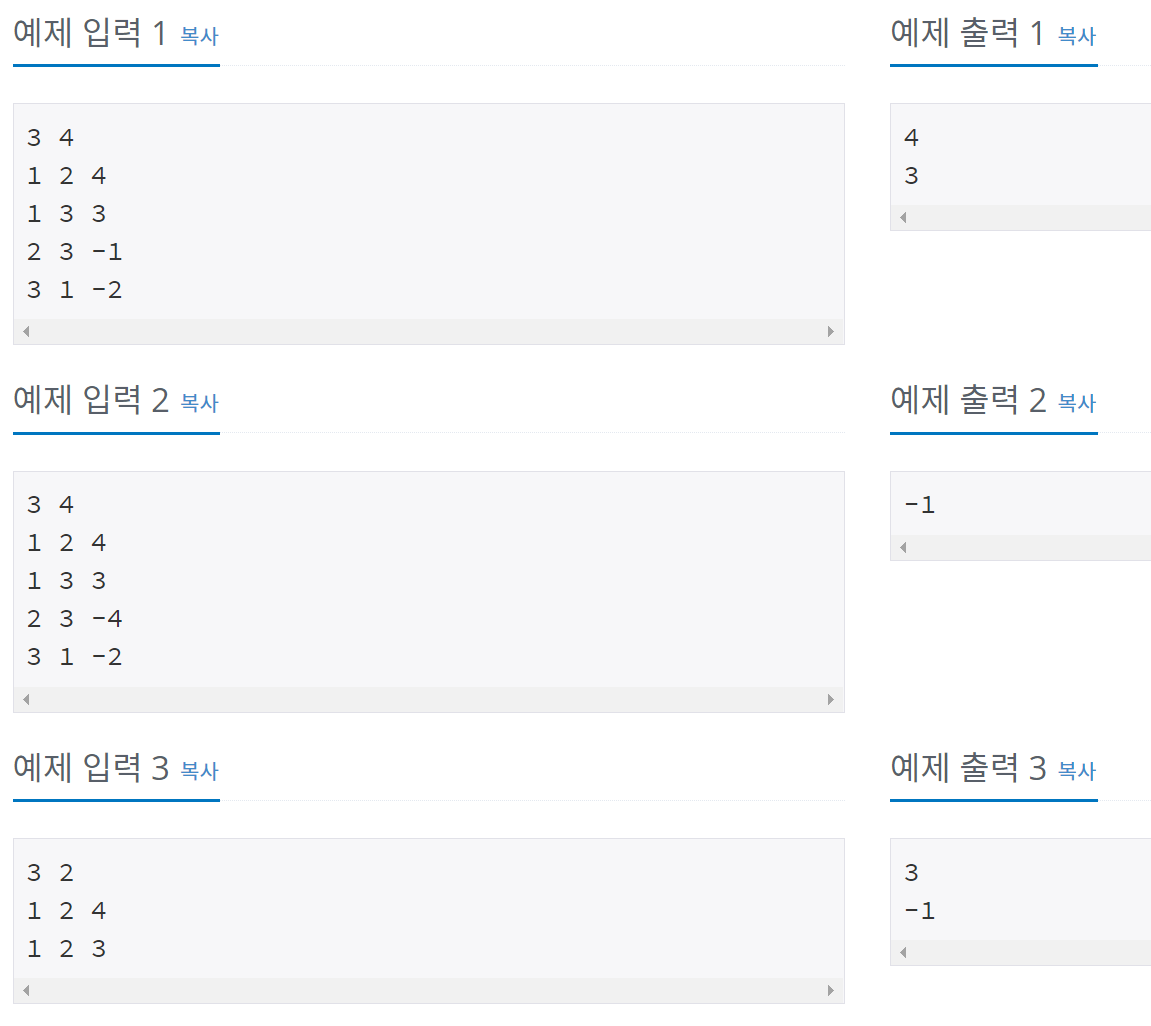
예제 입&출력

---

소스코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

public class Main {
    private static int n, m;
    private static Info[] infos;
    private static Long[] dist;
    private static final Long INF = Long.MAX_VALUE;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken());
        m = Integer.parseInt(st.nextToken());

        infos = new Info[m];
        dist = new Long[n + 1];
        Arrays.fill(dist, INF);

        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());

            int a = Integer.parseInt(st.nextToken());
            int b = Integer.parseInt(st.nextToken());
            int c = Integer.parseInt(st.nextToken());

            infos[i] = new Info(a, b, c);
        }

        if (!bellmanFord()) {
            System.out.println(-1);
        } else {
            for (int i = 2; i <= n; i++) {
                System.out.println(dist[i].equals(INF) ? -1 : dist[i]);
            }
        }
    }

    private static boolean bellmanFord() {
        dist[1] = 0L;

        /**
         * 최단 경로가 나올 수 있는 최대 간선 갯수는 N-1개이다. 
         * 벨만-포드 알고리즘은 시간 복잡도가 O(VE)이다. 
         * 모든 간선의 경우를 다 따져야 한다.
         */
        for (int i = 0; i < n - 1; i++) {
            for (int j = 0; j < m; j++) {
                Info info = infos[j];

                if (dist[info.s] != INF && dist[info.e] > dist[info.s] + info.cost) {
                    dist[info.e] = dist[info.s] + info.cost;
                }
            }
        }

        for (int i = 0; i < m; i++) {
            Info info = infos[i];

            if (dist[info.s] != INF && dist[info.e] > dist[info.s] + info.cost) {
                return false;
            }
        }

        return true;
    }

    private static class Info {
        int s;
        int e;
        int cost;

        public Info(int s, int e, int cost) {
            this.s = s;
            this.e = e;
            this.cost = cost;
        }
    }
}

---

Comment

• 지금까지 살펴봤던 다익스트라 알고리즘과는 조금 다르다. 음의 가중치(간선)는 자칫하면 음의 싸이클을 야기한다. 최단경로가 -∞을 야기한다. 이를 잘 살펴야 한다.
• 예를 들어
  
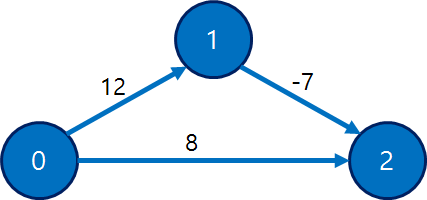
  • 이와 같은 그래프가 있을 때, 다익스트라 알고리즘은 0에서 2로 갈 때 dist[1] = 12 > dist[2] = 8이어서 2번 정점을 방문을 하고 최단 경로의 값을 8로 측정한다. 하지만 0 -> 1 -> 2는 5이다.
• 음의 경로가 있을 때는 벨만-포드 알고리즘을 사용해야 한다. 위의 문제는 전형적인 벨만-포드 알고리즘.
• 최단 경로를 구할 때 최대값이 4byte의 정수형을 넘기진 않지만 음의 싸이클이 존재할 때 무한적으로 값이 감소할 수 있다. (위의 문제의 경우 모든 간선의 가중치가 -10,000일 때) 그렇기에 8byte 정수형인 Long을 사용해야 출력 초과가 발생하지 않는다.

---