1st course: Neural Networks and Deep Learning

🗂 목차

• 1장: Introduction to Deep Learning

• 2장: Neural Networks Basics

• 3장: Shallow neural networks

• 4장: Deep Neural Networks

2. Neural Networks Basics

1. Binary Classification

• 이번 강의에서는 신경망 학습 과정에서 순전파와 역전파를 이용하여 계산하는 이유에 대해서 다루게 됨

  • 이전에는 m개의 학습 표본을 가진 학습 세트가 있으면, m개의 학습 표본에 대해서 for문을 돌리면서 순차적으로 학습 세트를 처리했음

  • 하지만 신경망을 구현할 대는 전체 학습 세트를 학습하는데 for문을 사용하지 않고 처리하고자 함

• 특정 이미지에서 고양이가 아닌지 구분하는 문제는 이진 분류 문제임

  • output으로는 고양이 일 때는 1, 고양이가 아닐 때는 0으로 출력됨

  • 이미지는 컴퓨터에서는 각각 빨간색, 녹색, 파란색 채널에 대응하는 64x64차원의 3개 행렬로 인식하게 됨

  • 그리고 input으로 들어가는 x의 특징 벡터는 64x64x3의 차원에 해당하는 12,288개의 모든 픽셀값이 다음과 같이 표현될 수 있으며 해당 이미지의 벡터화를 통해 데이터를 학습하고 1과 0을 예측하게 됨

2. Logistic Regression

• 로지스틱 회귀분석은 output, y를 1과 0으로 예측하는 지도학습 알고리즘임

  • 로지스틱 회귀분석의 목표는 예측값과 실제값의 오차를 최소화 하는 것임

  • 데이터를 가지고 실제값을 학습하여 예측하는 과정에서 해당 input 데이터의 특징 벡터가 y값을 가지는 확률의 정도를 가지게 됨

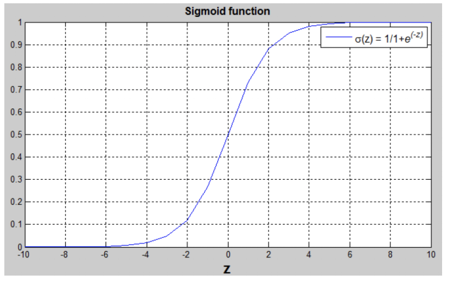
• 이 때, y가 1과 0으로 예측되는 확률을 0-1 사이의 값으로 추정되야 하기 때문에 시그모이드 함수를 적용해 줄 수 있음

  • 시그모이드 함수는 어떤 양 Z에 대한 0-1 범위를 반환해주는 함수를 말하며, Z의 값이 매우 크면 1에 가까울 것이고 작을수록 0에 가까워짐

  • 로지스틱 회귀분석에서는 파라미터 W와 B를 배워서 y hat이 Y에 대한 확률을 잘 추정한 수치가 나오도록 하는 것임

3. Logistic Regression cost function

• 로지스틱 회귀분석 모델에서 학습을 통해 파라미터를 업데이트하기 위해서는 cost function에 대한 정의가 필요함

  • 각 데이터 i에 대한 예상값 y hat(i)과 실제값, ground true인 y(i)의 비교를 통해 알고리즘의 정확도를 파악하기 위해서 loss fuction 혹은 error function을 적용할 수 있음

  • loss function의 한가지 방법으로는 (y(i) - y hat(i))의 제곱 혹은 0.5*제곱으로 구할 수 있음

  • 하지만 이 방법은 convex optimization problem이 존재하여 gradient descent가 잘 해결되지 않는다는 단점이 존재함(추후 optimization 강의에서 다룰 것으로 언급)

• 그렇기 때문에 로지스틱 회귀분석에서는 다음과 같은 로지스틱 회귀의 loss function을 사용함

  • 다음 식은, 실제값 y가 0과 1일 때의 경우를 구분해서 어떻게 비용이 발생되는지 확인할 수 있음

  • y = 1 일 경우: 좌측 항인 -log(y hat)만 남아있으며 해당 식이 작은 값을 가지기 위해서 y hat은 가질 수 있는 범위의 최대인 1로 향할 때, 비용이 0으로 수렴함

  • y = 0 일 경우: 우측 항인 log(1-y hat)남 남아있으며 해당 식이 작은 값을 가지기 위해서 y hat이 가질 수 있는 범위의 최소인 0으로 향할 때, 비용이 0으로 수렴함

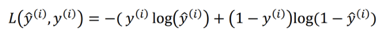
• 해당 식을 전체 학습 세트에 적용하여 평균치를 구하게 됨으로써 알고리즘의 작동 여부를 측정하게 되고 그것을 cost function이라 부르고,cost function을 최소화 하는게 해당 문제에서의 목적이 될 것임

  • loss function은 하나의 학습 데이터에 대한 오차를 말하며, cost function은 전체 학습 데이터에 대한 loss function의 평균을 말함

4. Gradient Descent

• 앞서 살펴본 로지스틱 회귀분석의 cost function인, J(w, b)를 최소화하는 파라미터 w, b를 찾아가는 과정이 Gradient Descent임

• 해당 cost function은 convex function으로 하나의 볼록한 그릇 모양이라고 할 수 있음

  • 시작점을 시작으로 기울기 강하의 반복 작업을 통해서 global optimum에 도달할 수 있게 됨

  • 해당 함수는 convex function이므로, 시작점의 위치에 따라 최종적으로 도달하는 지점이 크게 다르지 않음

• global optimum을 찾아가는 과정을 다음과 같이 간단하게 살펴볼 수 있음

  • gradient descent가 반복 과정을 거치게 되면서 global optimum을 찾아갈 수 있는 이유는 특정 지점의 기울기와 방향, 그리고 learning rate의 계산을 통해서 global optimum을 찾아갈 수 있음

  • 그렇기 때문에 해당 그래프에서 좌우측, 그리고 시작 지점이 다르게 되어도 정해진 learning rate와 기울기로 계산되는 비용의 최소점을 찾기 위해서 최종적으로 비슷한 지점이라는 결과가 나옴

5. Derivatives

• gradient descent에서는 해당 지점의 기울기를 바탕으로 비용을 최소화하는 과정을 거치는데, 한 점의 기울기 값을 구하기 위해서는 미분학에 대한 이해가 필요함

• 기울기에 대한 아주 간단한 이해를 위해 다음 그래프를 볼 수 있음

  • 기울기란 x 이동량만큼의 y 이동량의 정도를 의미하며 해당 직선에서는 어느 지점에서도 같은 기울기를 가지게 됨

6. More Derivative Examples

• 함수의 기울기가 지점마다 달라지는 경우가 있음

  • 다음과 같은 그래프에서는 x=2일 경우가 x=5일 경우에 기울기가 각각 4와 10으로 달라지는 것을 볼 수 있음

  • 이 때, 해당 지점의 기울기는 함수가 미분된 형태에서 대입해 구할 수 있는 것과 똑같음을 알 수 있음

7. Computation Graph

• 신경망의 계산법은 forward pass 또는 전 방향전파 step 방식으로 이루어지기 때문에 신경망의 결과값을 계산하여 backward pass 또는 후 방향전파 step 방식으로 기울기인 미분값을 계산함

• 이러한 계산 방식의 구조를 계산 그래프를 통해 확인해 볼 수 있음

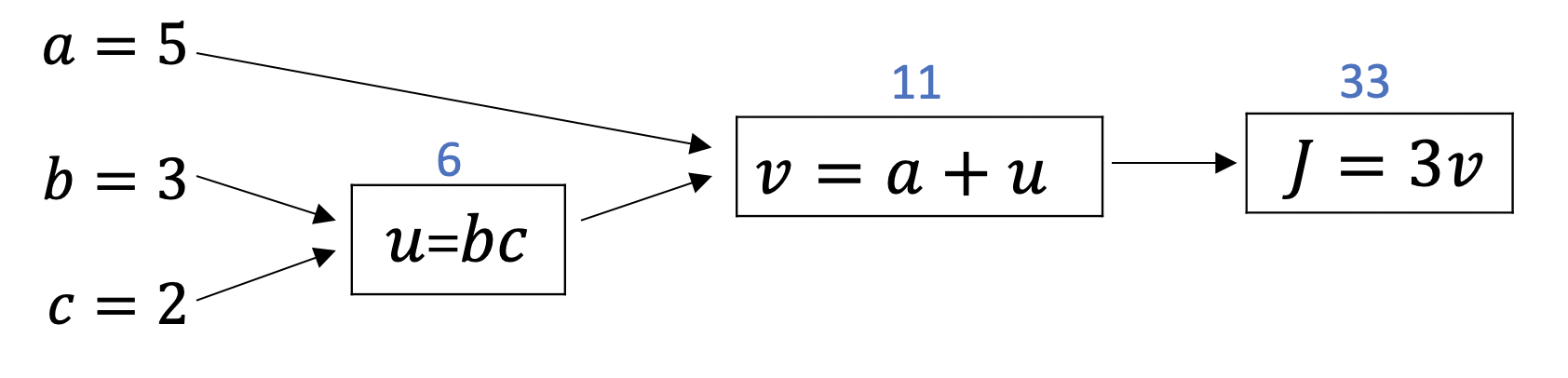
  • a,b,c를 변수로 가지는 F = 3(a + b*c)라는 함수가 존재 할 때, 계산이 되는 과정을 다음과 같이 도식화 할 수 있음

  • 이 간단한 예제를 통해서, 왼쪽에서 오른쪽으로 계산되는 과정이 F를 구할 수 있는 방식이기 때문에 왼쪽에서 오른쪽으로 반대 방향으로 변화량에 대한 미분값을 구할 수 있는 방법이 됨