P4 1854 K번째 최단경로 찾기

33분 57초
다익스트라 알고리즘을 정확하게 이해해야 풀 수 있었던 문제.
i번째 도시에 도착했을 때 k번째 최단경로까지만 저장한다는 것이 핵심 아이디어이다.
만약 저장된 거리 수가 k보다 작다면 그냥 저장하고, 저장된 거리 수가 이미 k개로 꽉 찼다면 k번째 최단거리와 비교했을 때 작으면 해당 k번째 최단거리를 pop하고 새로운 최단거리를 추가한다.

코드

priority_queue<int, vector<int>, less<>> d[1001];

void dijkstra(int start) {
    d[start].emplace(0);
    priority_queue<pii, vector<pii>, greater<>> pq;
    pq.emplace(0,start);
    while(!pq.empty()) {
        int here = pq.top().s;
        int dist = pq.top().f;
        pq.pop();

        if(d[here].size() == k && d[here].top() < dist) continue;
        for(pii edge : g[here]) {
            int there = edge.f, nextDist = dist + edge.s;
            if(d[there].size() == k) {
                if(d[there].top() <= nextDist) continue;
                else d[there].pop();
            }
            d[there].emplace(nextDist);
            pq.emplace(nextDist, there);
        }
    }
}

P4 11266 단절점

2시간 18분 7초
단절점이란, 해당 노드를 비활성화시켰을 때 connected component의 개수가 증가하는 정점을 말한다.
단절점의 조건은 다음과 같다.

• root 노드일 때
  1. 자식 subtree가 2개 이상인 경우
• root가 아닌 노드일 때
  1. 자식 subtree가 존재하며
  2. 자식 subtree들 중 적어도 하나가 lowest 역방향 간선이 해당노드보다 자식노드인 경우
  

자식 subtree들 중 적어도 하나가 lowest 역방향 간선이 해당노드보다 자식노드인 경우
이 말을 좀 더 쉽게 설명하자면,
자식 subtree들 중 하나라도 역방향으로 올라갈 수 있는 lowest한(방문 순서 값이 낮은) 노드가 현재 노드보다 자식이라면 해당 노드는 단절점이 된다.

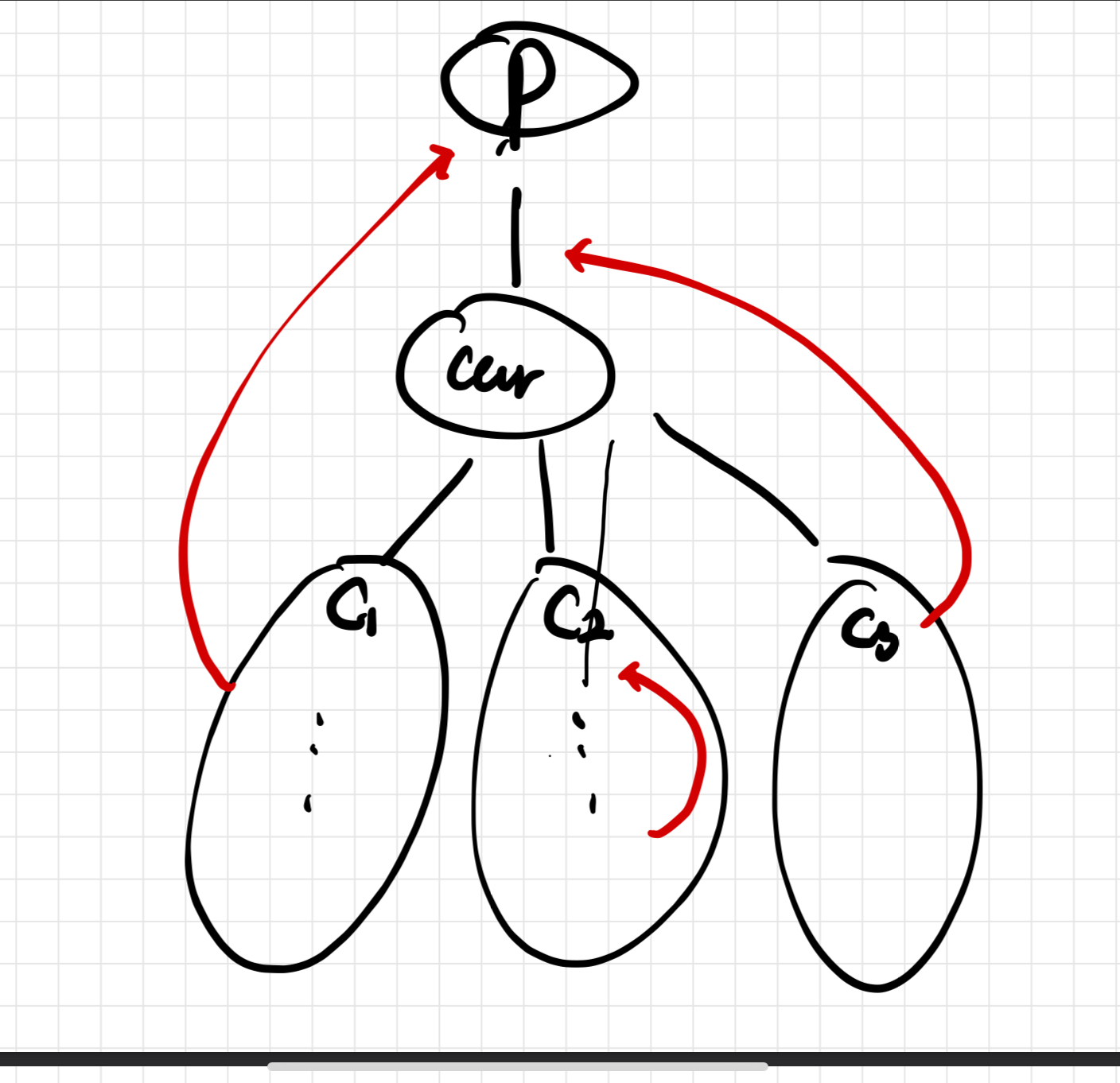
위 그림을 보면 subtree2의 경우 lowest 역방향 간선이 cur의 parent들에 연결되지 못하므로 cur 노드가 비활성화 되면 subtree2는 분리되게 된다. 따라서 cur노드는 단절점이 된다.

코드

// 역방향 간선이 올라가는 가장 높은 노드를 반환
int dfs(int here, int seq) {
    visited[here] = seq;
    int child = 0;
    int low = 0, ret = seq;

    for(int there : g[here]) {
        // 새로운 subtree 생성
        if(visited[there] == 0) {
            child++;
            int res = dfs(there, seq+1);
            low = max(low, res);
            ret = min(ret, res);
        }
        else ret = min(ret, visited[there]);
    }
    if((seq == 1 && child >= 2) || (seq > 1 && child != 0 && seq <= low)) ans.emplace_back(here);
    return ret;
}

결론

단절점 문제는 DFS탐색을 통해서 역방향 간선을 주목해야 풀 수 있다.
그리고 단절점이 되는 경우를 잘 생각하고 특히 위 그림의 경우가 헷갈릴 수 있는데 이를 잘 이해하고 구현해야 풀 수 있는 문제였다.