P4 11400 단절선

15분
저번에 풀었던 단절점과 연관되어 있는 단절선 문제이다.

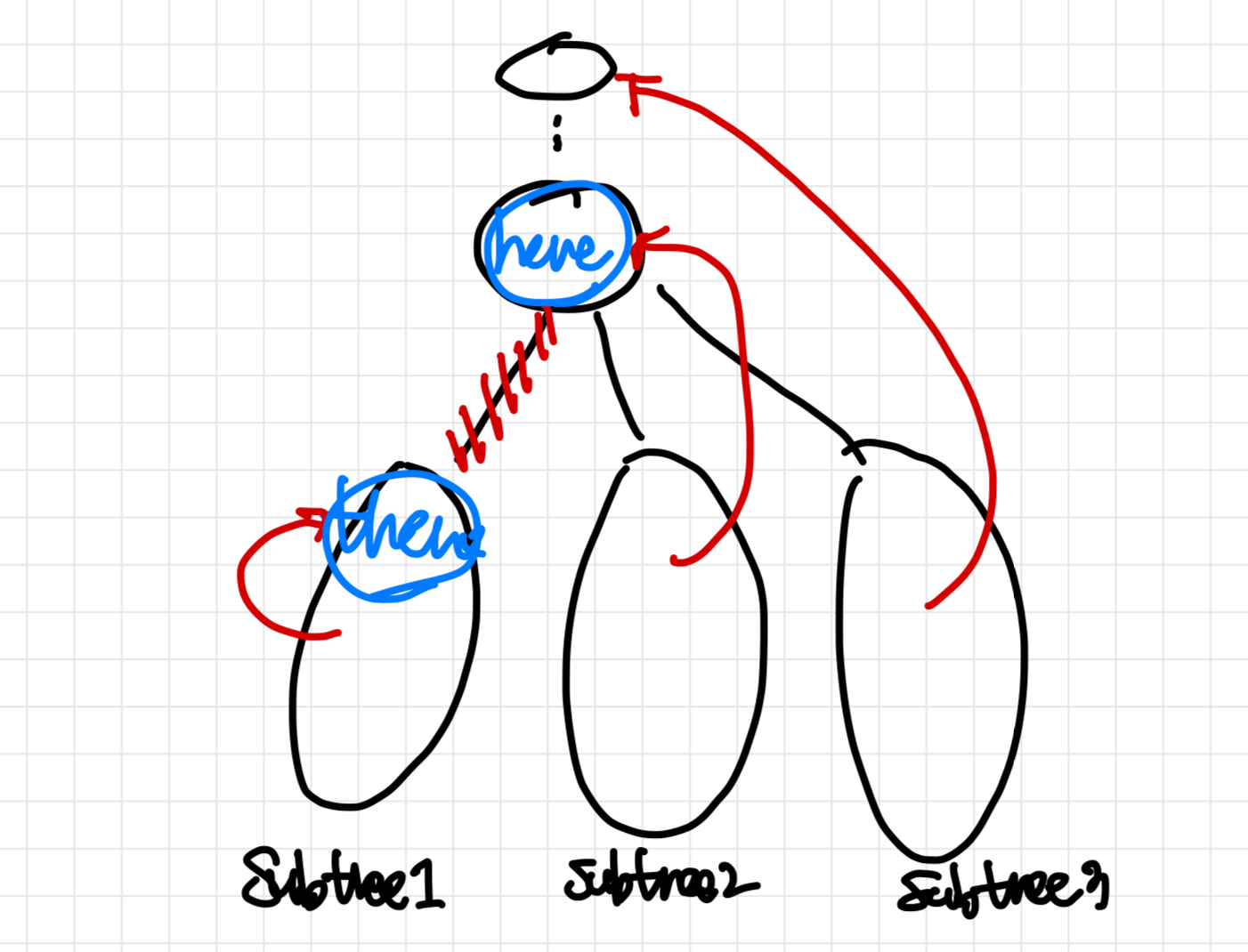
위 그림에서 subtree1의 lowest 역방향 간선이 here보다 자식이기 때문에 here-there 를 잇는 간선을 끊으면 subtree1은 분리된다. 따라서 here-there 간선이 단절선이 되는 것이다.
단절점과는 달리 root 노드여도 해당 조건은 그대로 적용된다. here 노드 자체에 연결되는 역방향 간선만 존재한다면 분리되지 않기 떄문이다. 따라서 부모 노드가 없는 root 노드도 상관없이 적용된다.

int visited[mxn];
vector<int> g[mxn];
vector<pii> ans;

int dfs(int here, int seq) {
    visited[here] = seq;
    int ret = seq;
    for(int there : g[here]) {
        if(visited[there] == seq-1) continue; // 직속 부모는 뺀다.
        if(visited[there] == 0) {
            int res = dfs(there, seq+1);
            if(seq < res) ans.emplace_back(min(here,there), max(here, there));
            ret = min(ret, res);
        }
        else ret = min(ret, visited[there]);
    }
    return ret;
}

P4 1305 광고

55분 17초
kmp 알고리즘의 pi배열을 이용하면 풀리는 문제다.

pi 배열이란 해당 string에 대해서 prefix == suffix인 가장 긴 길이를 저장하는 배열이다.
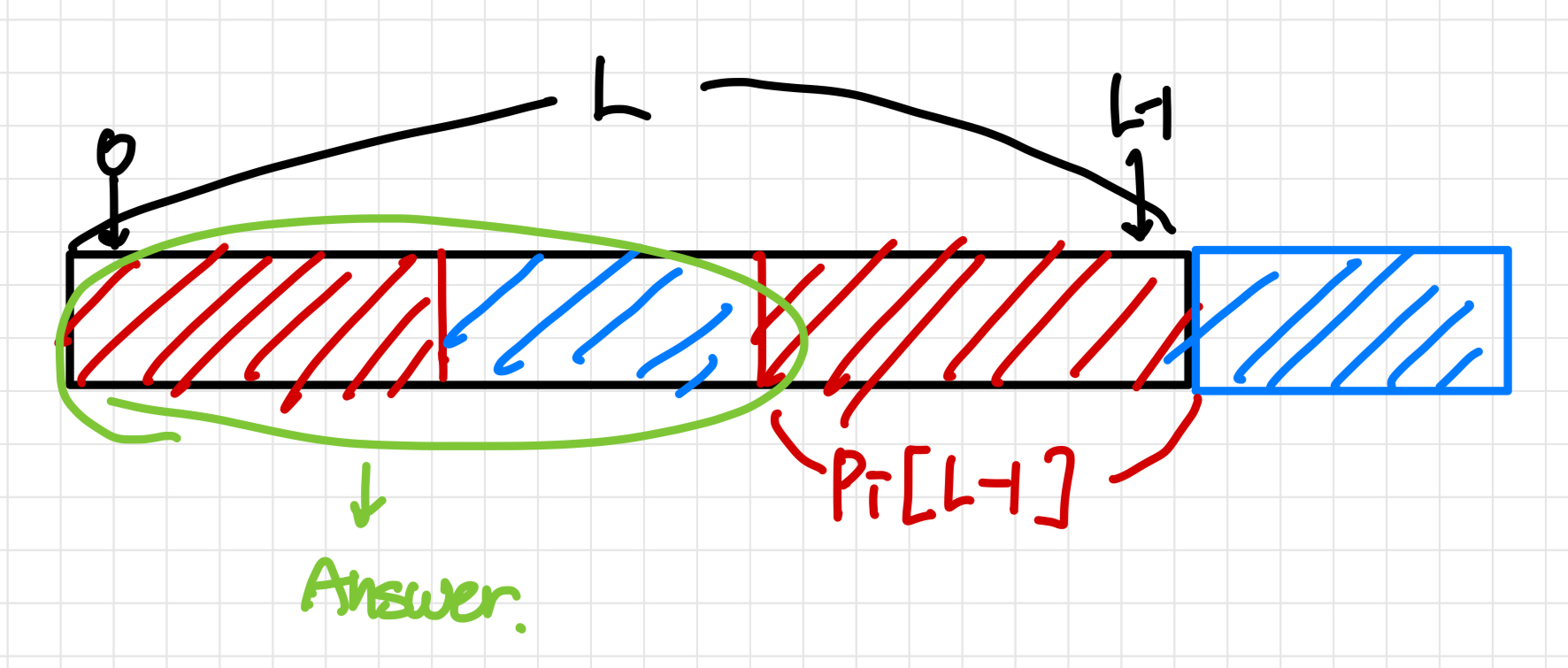
따라서 길이가 L인 광고판 문자열의 pi[L-1]을 구했을 때, [빨간색 박스] + [파란색 박스]가 원래 광고가 가능하다.
여기서 pi 배열의 정의에 따르면 [빨간색 박스]는 해당 문자열에 대해서 가장 긴 일치하는 부분이므로 [빨간색 박스] + [파란색 박스]가 가능한 광고의 길이 중 가장 짧은 값이 된다.

int L;
string S;

vector<int> getPi(string p) {
    int j=0;
    vector<int> pi(L, 0);
    for(int i = 1; i < L ; i++) {
        while(j > 0 && p[i] !=  p[j]) j = pi[j-1];
        if(p[i] == p[j]) pi[i] = ++j;
    }
    return pi;
}

// main 함수 
	cin >> L >> S;
    vector<int> pi = getPi(S);
    cout << L - pi[L-1] << '\n';

참고

• kmp 알고리즘 및 pi 배열
  https://bowbowbow.tistory.com/6
• boj 1305 풀이
  https://uang.tistory.com/33