PS

30분 23초세그먼트 트리 문제인 것이 한눈에 보인다.곱했을 때 양수, 음수, 0으로만 구별하므로 양수면 1, 음수면 -1로 바꿔서 저장한다.1시간 14분 9초슬라이딩 윈도우를 생각했다가 어떻게 구현할지 생각을 못해내서 세그먼트 트리로 풀었다.알고보니 deque를 사용

20분 11초맛 번호의 개수를 가지고 있는 세그먼트 트리를 이용하여 해결한다. 즉, tree1:= 맛 1 ~ 1,000,000의 모든 개수 가 된다. x 번째로 맛있는 사탕을 찾고 싶으면 tree2\*node의 값 보다 작으면 왼쪽 child로, 그렇지 않다면 오른쪽

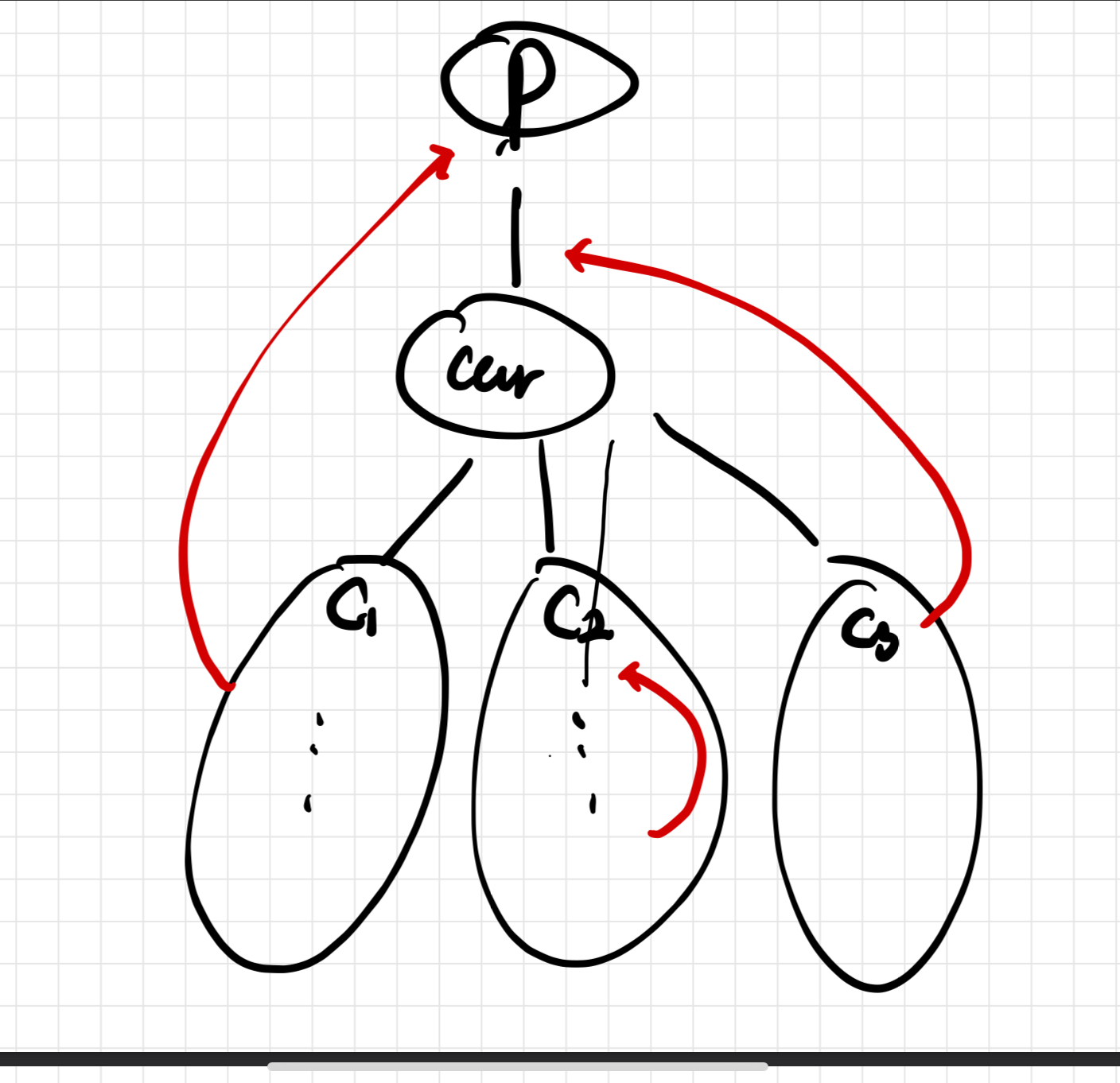
P4 1854 K번째 최단경로 찾기 P4 11266 단절점

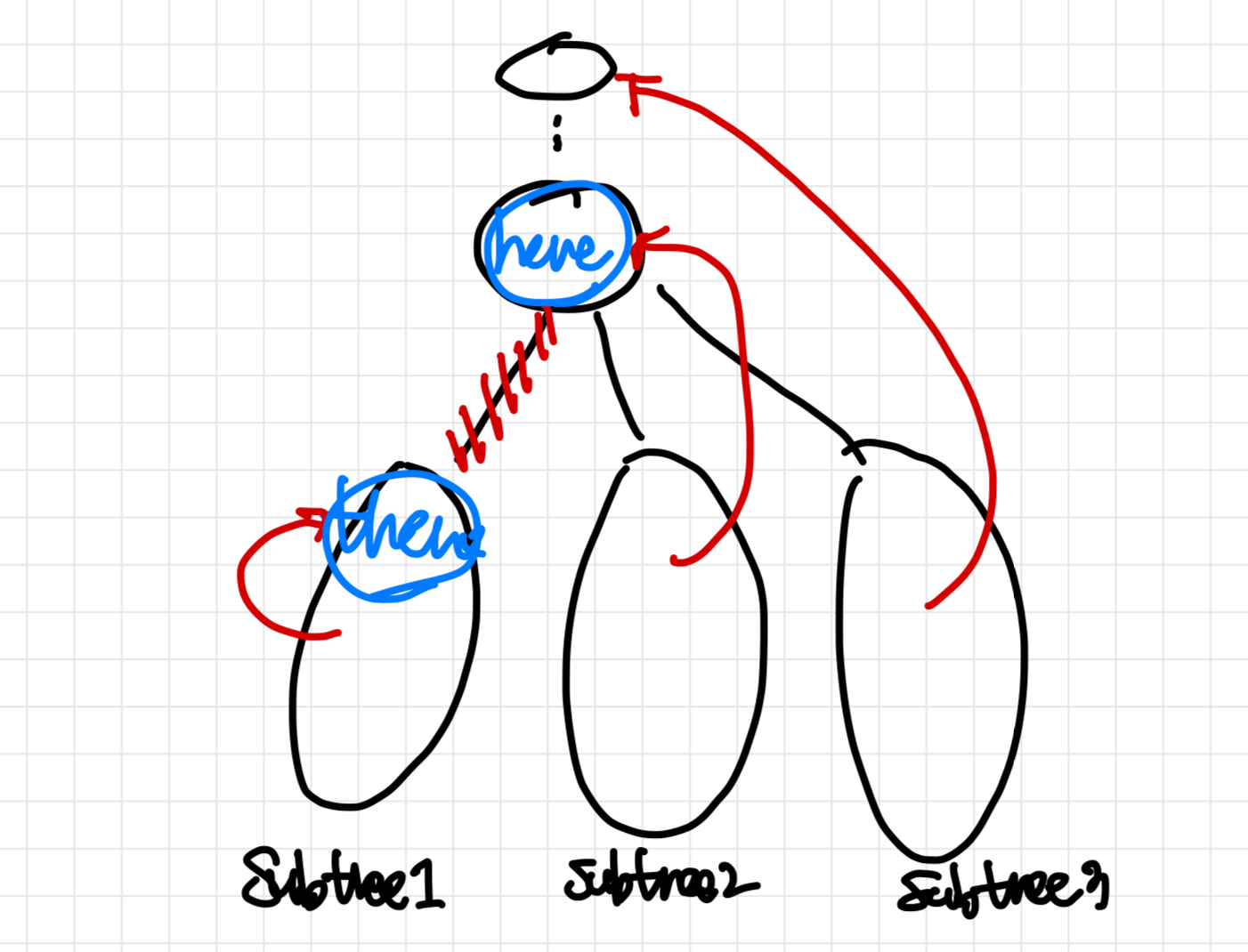
15분저번에 풀었던 단절점과 연관되어 있는 단절선 문제이다. 위 그림에서 subtree1의 lowest 역방향 간선이 here보다 자식이기 때문에 here-there 를 잇는 간선을 끊으면 subtree1은 분리된다. 따라서 here-there 간선이 단절선이 되는 것

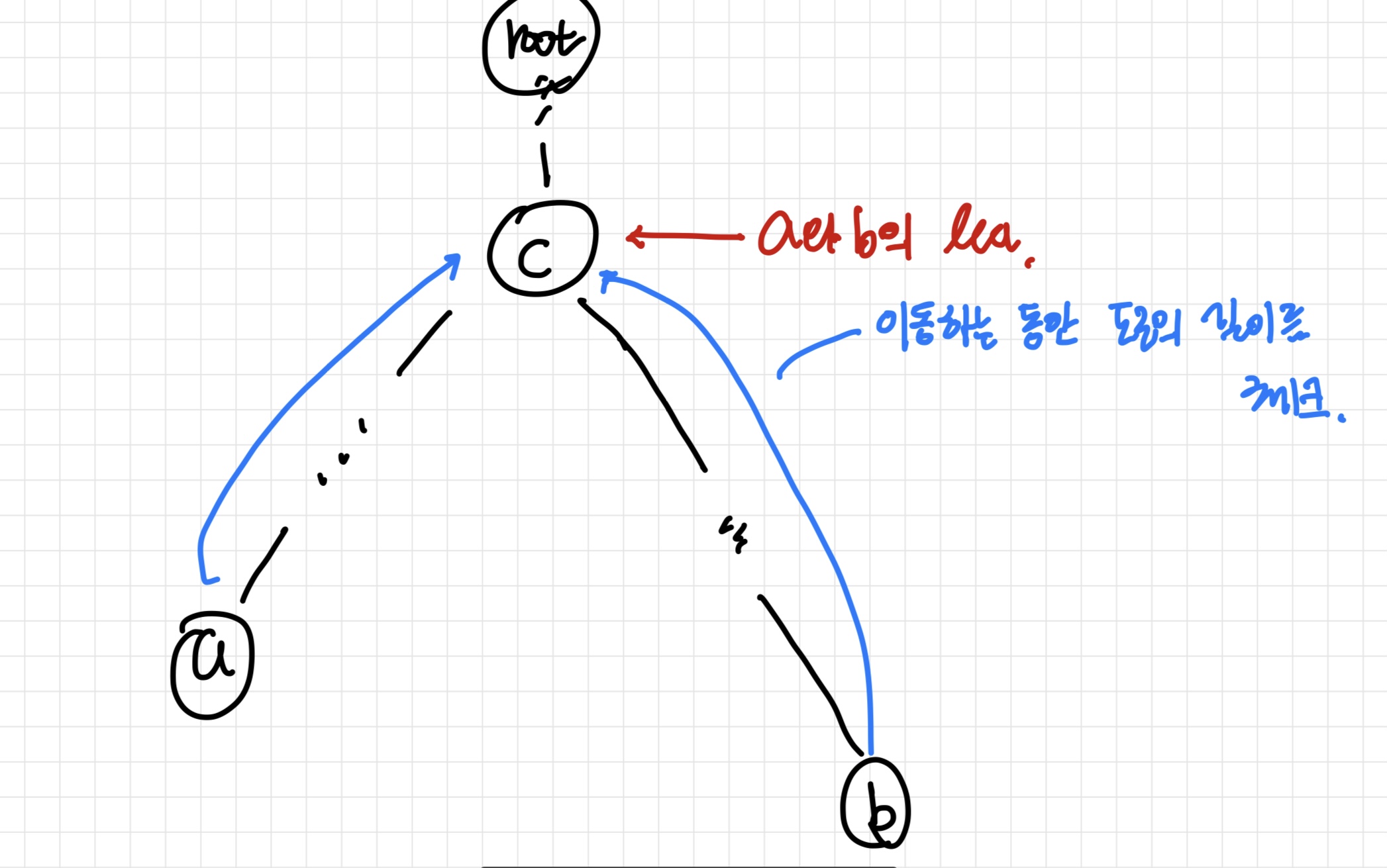
1시간 17분 45초트리의 최소 공통 조상(Lowest Common Ancestor)를 찾아서 해결하는 문제이다.그냥 dist10^510^5를 최소 사용하면 4000MB의 메모리가 필요하므로 불가능하다. 따라서 거리를 저장하지 않고 질문이 들어올 때마다 계산해서 반환해

19분 6초구간 변경이 요구되는 문제다. 느리게 갱신되는 세그먼트 트리를 사용하면 풀릴 것이 보였다.1시간 34분 36초보자마자 Trie인 걸 알았으나 일반적인 정적 배열로 child를 만들면 메모리 초과가 된다. vector나 unordered_map으로 구현하면 이

2시간 51분 50초고도를 정렬하고 중복 제거 한 후 투포인터를 이용해서 차이가 가장 적은 고도를 구하는 문제다.투포인터도 생각 못하고 탐색 알고리즘으로 삽질해서 시간을 말도 안 되게 소모했다. 반성하자.left, right 투 포인터를 이용해 가장 차이가 적은 고도의

1시간 2분 32초마을의 지도를 1번 집이 root가 되도록 트리로 그렸다. 이떄 각 집마다 가장 적은 비용을 들게 하는 색 c1과 두 번째로 적은 비용을 들게 하는 색 c2를 저장하도록 한다.만약 부모 집의 색과 현재 집의 c1이 다르다면 그냥 c1을 칠하면 되고,부

보자마자 빡빡한 구현일 것을 직감하였다. 하지만 이런 쉬운 난이도에 빡구현인 문제는 왜 이렇게 하기 싫은걸까.. 다른 분들 코드도 구글링해 보았는데 1개 밖에 못 찾았고 그 분은 빡구현으로 하신 듯 했다.괜히 효율적으로 코딩하고 싶은 마음이 들어서 삽질을 해 보았고

1시간 55분 41초모든 정점들이 연결되지 않은 상태에서 경로를 연결한다고 생각하면 풀린다.query에서 부모노드와 분리하는 명령어는 query를 반대 순서로 보면 연결되어 있지 않은 트리에서 하나씩 부모노드와 연결하는 것과 같다.연결되어 있지 않은 트리에서 시작하는

44분 51초1년에 한 번씩 문명칸에 인접한 칸들이 새로운 문명이 되는 문제다. 이 부분은 익숙하다.다만 서로의 문명이 fully-connected 되었는지를 확인하기 위해 union-find를 사용해서 푸는 문제다.주의해야 할 점은 1년이 지나서 새로운 칸에 문명을

12분 46초(세그먼트 트리) 18분 18초(펜윅트리)보자마자 구간합이라는 것을 알았고 그냥 펜윅트리나 세그먼트 트리를 사용하면 간단히 풀린다.시간은 동일하고 메모리는 확실히 펜윅트리가 유리하다.

1시간 31분 3초보자마자 느리게 갱신되는 트리임을 알았지만 구현력이 딸려서 오래 걸렸다.lazy를 검사하고 갱신하는 코드를 매 노드에 접근할 때마다 했어야 했다.

57:10처음에는 이분매칭의 in과 out에서 아이디어를 얻었다.상어 a에 대하여 상어 a가 안 먹혔으면 ina = -1(초기값), 먹혔으면 ina = (상어 a를 먹은 상어의 번호)를 저장한다. 그런데 사실 여기서 out은 필요 없다.상어를 최대한 많이 먹어야 하므로

느리게 갱신되는 세그먼트 트리를 이용하여 푼다.느리게 갱신되는 세그먼트 트리를 사용할 때는 항상 lazy 값을 업데이트 시켜준 다음 뭔가를 할 수 있다.

세그먼트 트리 문제인데 query의 순서를 정렬하면 해결된다.합을 출력할 때 k의 순서가 오름차순이 되도록 정렬하고 ans 배열을 만들어 원래의 인덱스에 값을 넣어 원래 순서대로 출력하면 된다.조심해야 할 부분은 구간합이 10^5 \* 10^6 == 10^11으로 in

22:17구간 변경을 요구하므로 느리게 갱신되는 세그먼트 트리(lazy segment)를 이용하면 풀린다.주의할 점) lazy 값을 자식들한테 넘겨줄 때 자식들이 있는지 없는지 부터 확인해야 함 -> out-of-bounds 됨.

세그먼트 트리에 터보소트를 적용시키지 않은 값의 개수을 저장한다.vi = x라 할때 x를 앞으로 움직이려면 tree1~i-1 의 값만큼 움직여야 하고x를 뒤로 움직이려면 treei~n-1 의 값만큼 움직여야 한다.움직이고 나면 i번째 값은 트리에서 0으로 바꿔준다.

01:42:24최소값을 저장하는 세그먼트 트리를 사용하는데 그냥 사용하면 안 되고 발상의 전환이 필요하다.모든 학생들의 번호를 1번 시험의 등수로 바꾼다.예를 들면, 1번 시험의 등수가 2 3 1 이면, 2등한 학생이 1번 학생이 되는 식이다.학생 번호를 1번 시험의