P4 3176 도로 네트워크

1시간 17분 45초
트리의 최소 공통 조상(Lowest Common Ancestor)를 찾아서 해결하는 문제이다.
그냥 dist[10^5][10^5]를 최소 사용하면 4000MB의 메모리가 필요하므로 불가능하다.
따라서 거리를 저장하지 않고 질문이 들어올 때마다 계산해서 반환해줘야 한다.
근데 질문의 수가 10^5이므로 도로의 길이를 구하는 프로그램은 O(logN)이어야 한다는 것을 깨달았다.

O(logN)으로 트리 노드를 탐색하는 방법으로 LCA를 떠올렸고 코드로 작성했다.
parent[i][j] := (i 노드에서 $2^j$만큼 위에 있는 부모 조상의 노드번호)를 구해서 저장하는 것이 LCA의 핵심이다.

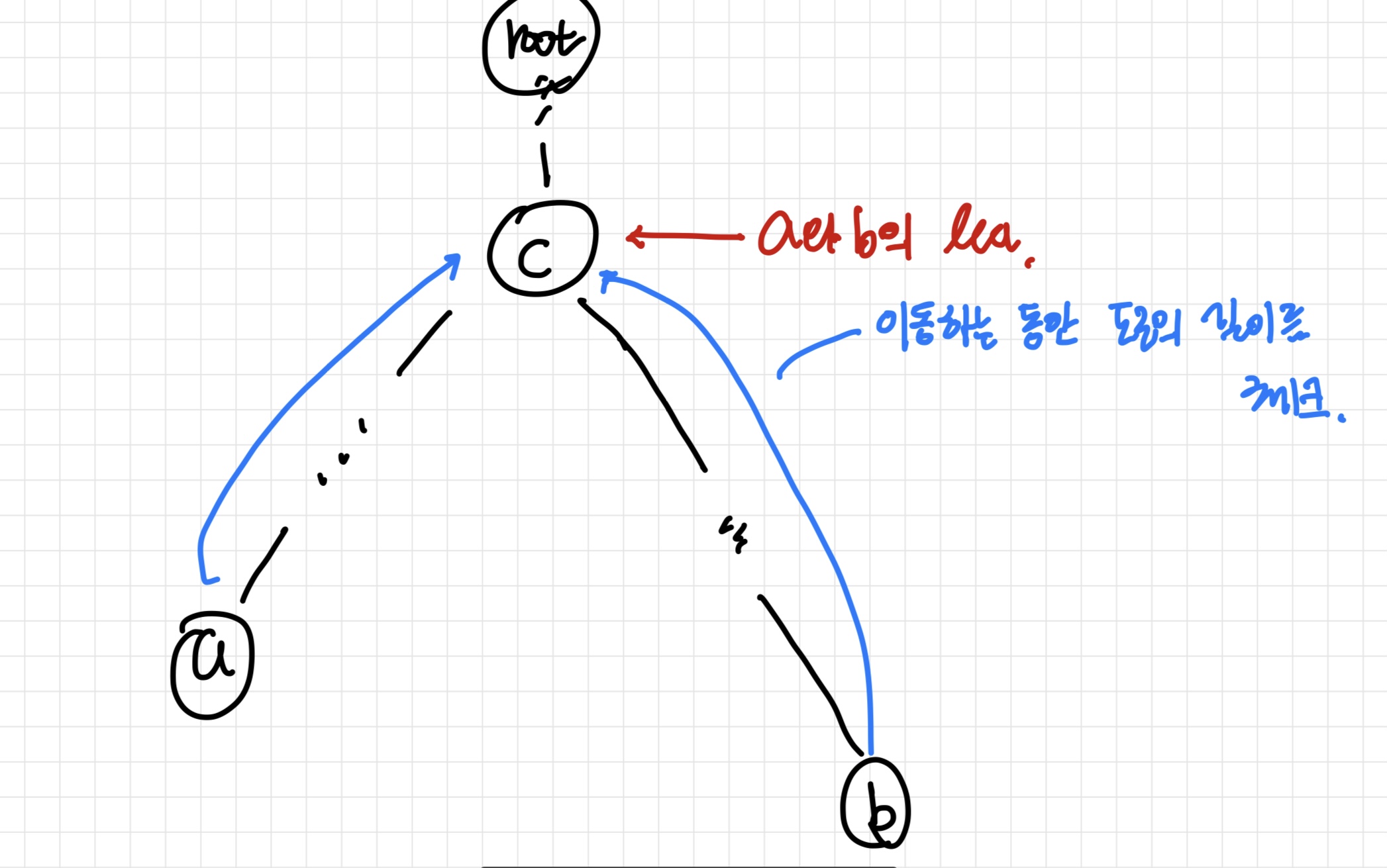
여기서 이 문제는 a - b의 최소, 최대 길이의 도로를 구하려면 c를 a와 b의 lca라 했을 때
a -> c와 b -> c 로 이동하는 동안의 도로를 모두 확인해주면 된다.

코드

pii val(pii a, pii b) {
    return pii(min(a.f,b.f), max(a.s,b.s));
}
void dfs(int here, int level) {
    lv[here] = level;
    for(pii next : g[here]) {
        int there = next.f, length = next.s;
        if(parent[here][0] == there) continue;
        parent[there][0] = here;
        dist[there][0].f = dist[there][0].s = length;
        dfs(there, level+1);
    }
}
// parent를 구하고, 움직일 때마다의 dist를 저장한다.
void setValues(int root) {
    parent[root][0] = root;
    dist[root][0] = pii(0,0);
    for(int j=1; j<LOGMXN; j++) {
        for(int i=1; i<=N; i++) {
            parent[i][j] = parent[parent[i][j-1]][j-1];
            dist[i][j] = val(dist[i][j-1], dist[parent[i][j-1]][j-1]);
        }
    }
}
// a와 b의 최소 공통 조상(Lowest Common Ancestor) 찾는 과정의 가장 짧고 긴 도로의 길이 반환
pii lca(int a, int b) {
    // b가 더 깊도록 설정한다
    if(lv[a] > lv[b]) swap(a,b);

    pii ret = pii(INF, 0);

    // a와 b의 깊이가 같게 만든다
    for(int i=LOGMXN-1; i>=0; i--) {
        if(lv[b]-lv[a] >= (1<<i)) {
            ret = val(ret, dist[b][i]);
            b = parent[b][i];
        }
    }

    // lca를 찾아서 반환한다
    if(a == b) return ret;
    for(int i=LOGMXN-1; i>=0; i--) {
        if(parent[a][i] == parent[b][i]) continue;
        ret = val(ret, val(dist[a][i], dist[b][i]));
        a = parent[a][i];
        b = parent[b][i];
    }
    return val(ret, val(dist[a][0], dist[b][0]));
}

후기

LCA의 parent 배열을 구하는 메커니즘을 제대로 기억하지 못한게 아쉽다.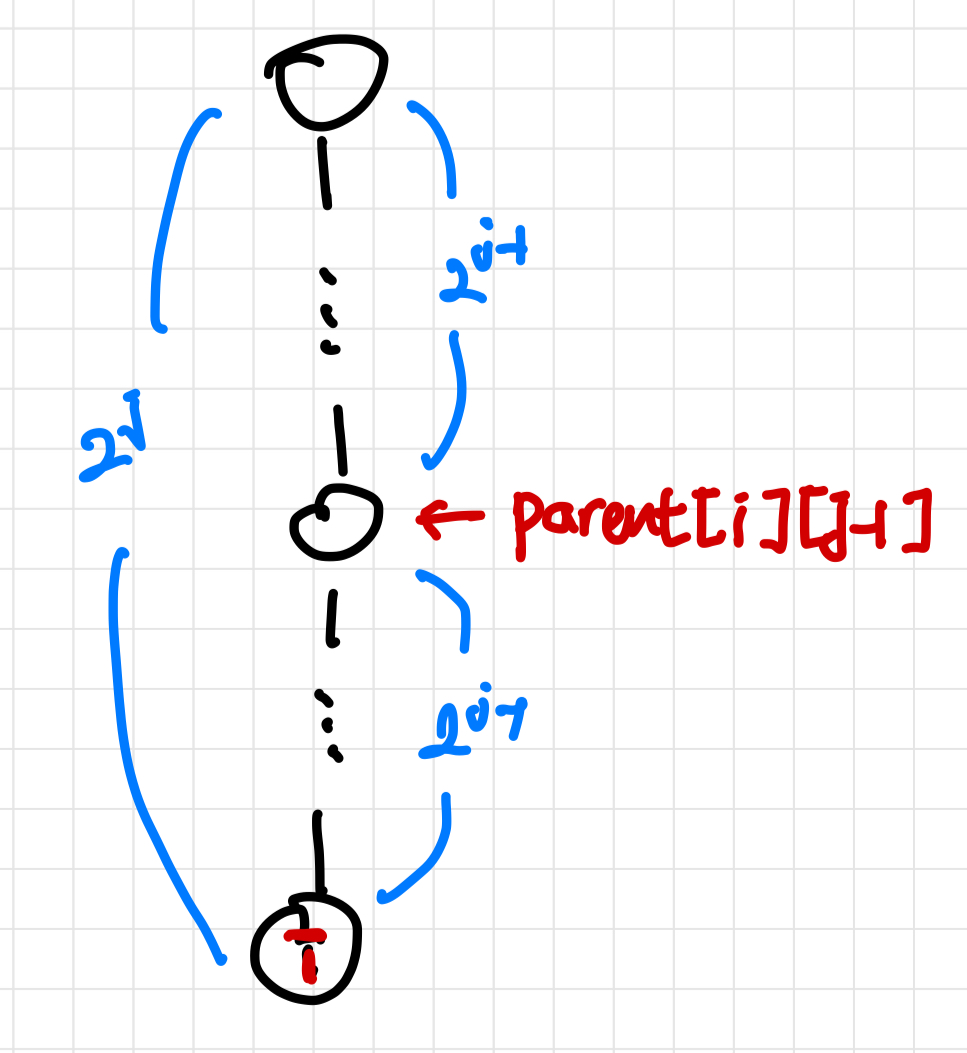위 그림을 보면 parent 배열 부분 코드를 이해하기 쉽다.

parent[i][j] = parent[ parent[i][j-1] ][ j-1 ]

여기서 주의할 점은 j를 바깥 for문으로, i를 안쪽 for문으로 넣어야 순서가 맞다. 모든 j-1에 대한 값을 알아야 다음 j에 대해서 계산할 수 있기 때문이다.

P4 3653 영화 수집

46분 0초
세그먼트 트리를 이용해서 풀 수 있는 문제다.

$i$번째 고른 영화를 $mv_i$라 하자.
$1 \leq x < i$ 일 때, $mv_x = mv_i$ 가 성립하는 가장 큰 x를 j라고 하자. (즉 $mv_i$ 영화를 가장 최근에 본 순서를 j라고 하자)

($mv_i$ 영화보다 위에 쌓여있는 영화의 개수) = ($j$+1 ~ $i$-1 순서에서 본 영화의 종류 개수)

($j$+1 ~ $i$-1 순서에서 본 영화의 종류 개수)을 세그먼트 트리를 이용하여 저장한다.
영화가 쌓여 있는 초기 상태는 1~n까지 순차적으로 쌓여 있으므로
이는 아무것도 쌓여있지 않은 상태에서 n->1의 순서로 영화를 봐서 쌓아올린 것과 같다.

예를 들어서 n=5이고 영화2 -> 영화1 -> 영화3 순으로 시청한다고 하자.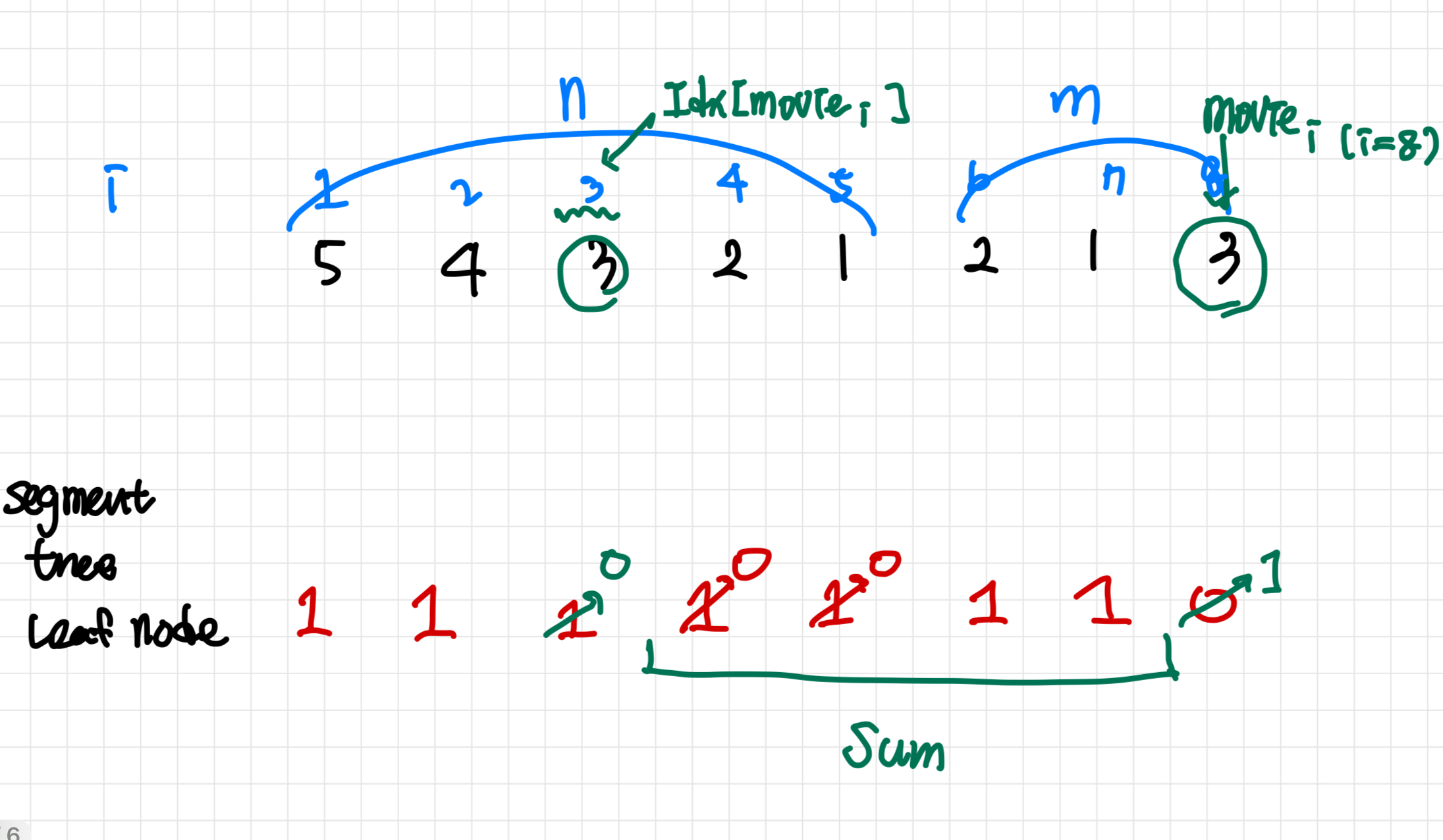3번 영화를 볼 때, 3번 영화 위에 쌓여있는 영화들의 개수는 $i$ = 4~7까지의 합과 같다.
그리고 세그먼트 트리에는 종류의 수를 저장하고 싶기 때문에 i=3일때의 leaf node를 0으로 바꾸고 i=8일 때의 leaf node를 1로 바꾸는 식으로 처리해준다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using tiii = tuple<int, int, int>;

class segment {
public:
    vector<ll> tree; //tree[node] := a[start ~ end] 의 합

    segment() {}
    segment(int size) {
        this->resize(size);
    }
    void resize(int size) {
        size = (int) floor(log2(size)) + 2;
        size = pow(2, size);
        tree.resize(size);
    }
    ll init(vector<ll> &a, int node, int start, int end) {
        if(start == end) return tree[node] = a[start];
        else return tree[node] = init(a, 2 * node, start, (start + end) / 2) +
                                 init(a, 2 * node + 1, (start + end) / 2 + 1, end);
    }
    ll sum(int node, int start, int end, int left, int right) {
        if(right < start || end < left) return 0;
        if(left <= start && end <= right) return tree[node];
        return sum(node * 2, start, (start + end) / 2, left, right) +
               sum(node * 2 + 1, (start + end) / 2 + 1, end, left, right);
    }
    void update(int node, int start, int end, int index, ll diff) {
        if(index < start || end < index) return;
        tree[node] += diff;
            update(node * 2, start, (start + end) / 2, index, diff);
            update(node * 2 + 1, (start + end) / 2 + 1, end, index, diff);
        }
    }
};

const int mxn = 1e5+1;
int n, m;
segment root(2*mxn);
int idx[mxn];
vector<ll> v;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int T; cin >> T;
    while(T--) {
        cin >> n >> m; m += n;
        for(int i=1; i<=n; i++)
            idx[i] = n+1-i;
        v.resize(0); v.resize(n+1,1); v.resize(m+1, 0);
        root.init(v, 1, 1, m);
        for(int i=n+1; i<=m; i++) {
            int movie; cin >> movie;
            if(idx[movie]+1 > i-1) cout << "0 ";
            else cout << root.sum(1,1,m,idx[movie]+1,i-1) << ' ';
            root.update(1,1,m,idx[movie],-1);
            root.update(1,1,m,i,1);
            idx[movie] = i;
        }
        cout <<'\n';
    }


    return 0;
}

참고

• LCA에 대해서
  https://blog.naver.com/ndb796/221282478466