2023.11.12. PS log

김진수·2023년 11월 12일

PS

목록 보기

11/19

P4 14868 문명

44분 51초
1년에 한 번씩 문명칸에 인접한 칸들이 새로운 문명이 되는 문제다. 이 부분은 익숙하다.
다만 서로의 문명이 fully-connected 되었는지를 확인하기 위해 union-find를 사용해서 푸는 문제다.

주의해야 할 점은 1년이 지나서 새로운 칸에 문명을 전파했을 당시에 인접해 있으면 연결된다는 점을 인식해야 한다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

const int MXN = 2e3;
const int KMXN = 1e5;

int N, K;
int board[MXN+1][MXN+1]; // 0: 미방문, 1~K: 문명의 번호
int parent[KMXN+1];
int dx[] = {1,-1,0,0};
int dy[] = {0,0,-1,1};
queue<pii> q;

bool outOfBound(int x, int y) {
    return !(1<=x&&x<=N && 1<=y&&y<=N);
}
int find(int idx) {
    if(parent[idx] == idx) return idx;
    return parent[idx] = find(parent[idx]);
}
bool merge(int a, int b) {
    a = find(a), b = find(b);
    parent[b] = a;
    return a != b;
}
void checkAdj() {
    queue<pii> tmp_q(q);
    while(!tmp_q.empty()) {
        int x = tmp_q.front().x, y = tmp_q.front().y;
        tmp_q.pop();
        for(int d=0; d<4; d++) {
            int nx = x+dx[d], ny = y+dy[d];
            if(outOfBound(nx,ny)) continue;
            if(board[nx][ny] == 0) continue;
            K -= merge(board[x][y], board[nx][ny]);
        }
    }
}
void year() {
    int sz = q.size();
    while(sz--) {
        int x = q.front().x, y = q.front().y;
        q.pop();
        for(int d=0; d<4; d++) {
            int nx = x+dx[d], ny = y+dy[d];
            if(outOfBound(nx,ny)) continue;
            if(board[nx][ny] != 0) {
                K -= merge(board[x][y], board[nx][ny]);
                continue;
            }
            board[nx][ny] = board[x][y];
            q.emplace(nx,ny);
        }
    }
}
void print() {
    cout << "K : " << K << '\n';
    for(int x=1; x<=N; x++) {
        for(int y=1; y<=N; y++) {
            cout << board[x][y];
        }
        cout << '\n';
    }
    cout << '\n';
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    //init
    memset(board, 0, sizeof board);
    for(int i=0; i<=KMXN; i++) parent[i] = i;

    cin >> N >> K;
    for(int i=1; i<=K; i++) {
        int x, y; cin >> x >> y;
        board[x][y] = i;
        q.emplace(x,y);
    }
    int ans = 0;
    checkAdj();
    while(K > 1) {
        year(); checkAdj();
        ans++;
    }
    cout << ans << '\n';


    return 0;
}

후기

checkAdj() 함수를 이용해서 year함수를 쓰기 전 초기상태에 대해서 한 번 적용시켜주고 매 year 함수가 끝날 때마다 chekcAdj()를 사용해주면 쉽게 풀린다.

P4 10266 시계 사진들

24분 7초
시계 침들이 모두 같은 모양과 길이이므로 결국 침들간의 각도 차이값이 더 중요하다.
(마지막 각도는 한 바퀴 돌고 나서의 첫번째 침까지의 각도 차이로 하면 된다.)
차이를 구하고 나면 시계1과 시계2의 순서가 다를 수 있다. 이를 시계1을 시계1+시계1로 바꾸고 시계2를 pattern으로 해서 kmp 알고리즘을 사용하면 풀 수 있다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

const int MXN = 36e4;
int n;
vector<int> clock1, clock2;

vector<int> getPi(vector<int> p){
    int m = (int)p.size(), j=0;
    vector<int> pi(m, 0);
    for(int i = 1; i< m ; i++){
        while(j > 0 && p[i] !=  p[j])
            j = pi[j-1];
        if(p[i] == p[j])
            pi[i] = ++j;
    }
    return pi;
}
bool kmp(vector<int> s, vector<int> p){
    auto pi = getPi(p);
    int n = (int)s.size(), m = (int)p.size(), j = 0;
    for(int i = 0 ; i < n ; i++){
        while(j>0 && s[i] != p[j]) j = pi[j-1];
        if(s[i] == p[j]){
            if(j==m-1) return true;
            else j++;
        }
    }
    return false;
}
int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    clock1.resize(n); clock2.resize(n);
    for(int i=0; i<n; i++) cin >> clock1[i];
    for(int i=0; i<n; i++) cin >> clock2[i];

    sort(all(clock1));
    clock1.emplace_back(clock1.front() + MXN);
    for(int i=0; i<n; i++) clock1[i] = clock1[i+1] - clock1[i];
    clock1.pop_back();

    sort(all(clock2));
    clock2.emplace_back(clock2.front() + MXN);
    for(int i=0; i<n; i++) clock2[i] = clock2[i+1] - clock2[i];
    clock2.pop_back();

    for(int i=0; i<n; i++) clock1.emplace_back(clock1[i]);
    if(kmp(clock1, clock2)) cout << "possible\n";
    else cout << "impossible\n";

    return 0;
}

후기

시계1과 시계2가 동일한 모양이지만 시작값이 달라서 발생하는 차이를 어떻게 확인할 것이지를 kmp로 해결해야 겠다는 생각을 하는 것이 핵십이었다.

P4 20149 선분 교차3

3시간 22분 14초
기하학과 선형대수학과 구현이 합쳐진 문제인데 개인적으로 너무 힘들었다.

선분 p1p2, 선분 p3p4의 교차여부와 교차점을 구한다고 하자.

1. 교차여부

(참고: https://killerwhale0917.tistory.com/6)
ccw를 이용하여 교차 여부를 확인한다.

1-1. $ccw_{\vec{p1p2}}$

$ccw_{\vec{p1p2}}$ 는 ccw(p1,p2,p3) * ccw(p1,p2,p4)로 확인한다.
$ccw_{\vec{p1p2}} \leq 0$ 이어야 직선 p1p2를 그었을 때 점 p3, p4가 서로 다른 영역에 속해있음을 알 수 있다. (등호일때는 직선 p1p2위에 존재한다는 뜻이다.)

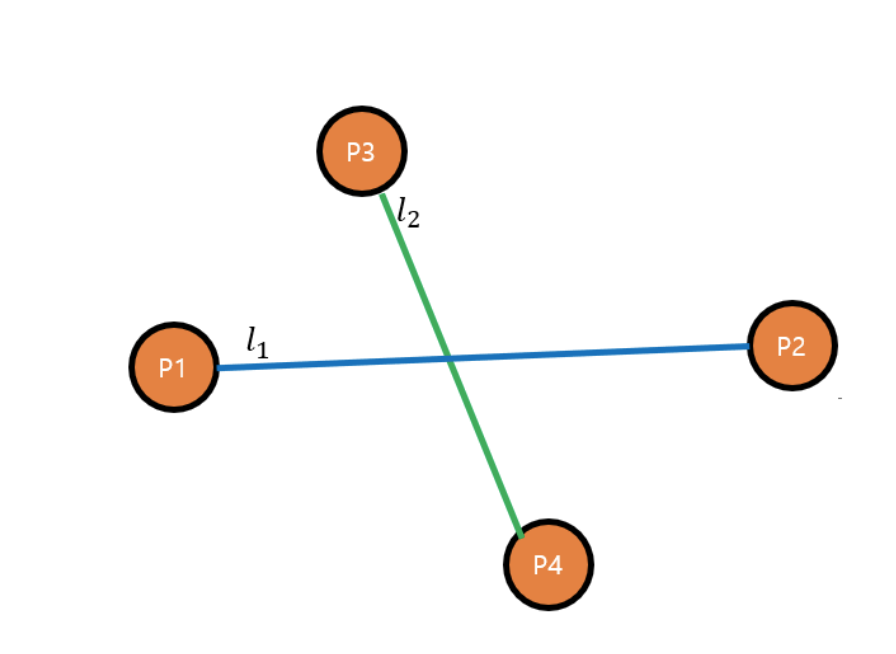
즉, $ccw_{\vec{p1p2}} = ccw(p1,p2,p3) \times ccw(p1,p2,p4) \le 0$

1-2. $ccw_{\vec{p3p4}}$

하지만 p1p2의 ccw만으로는 부족하다 아래와 같은 케이스가 있을 수 있기 때문이다.

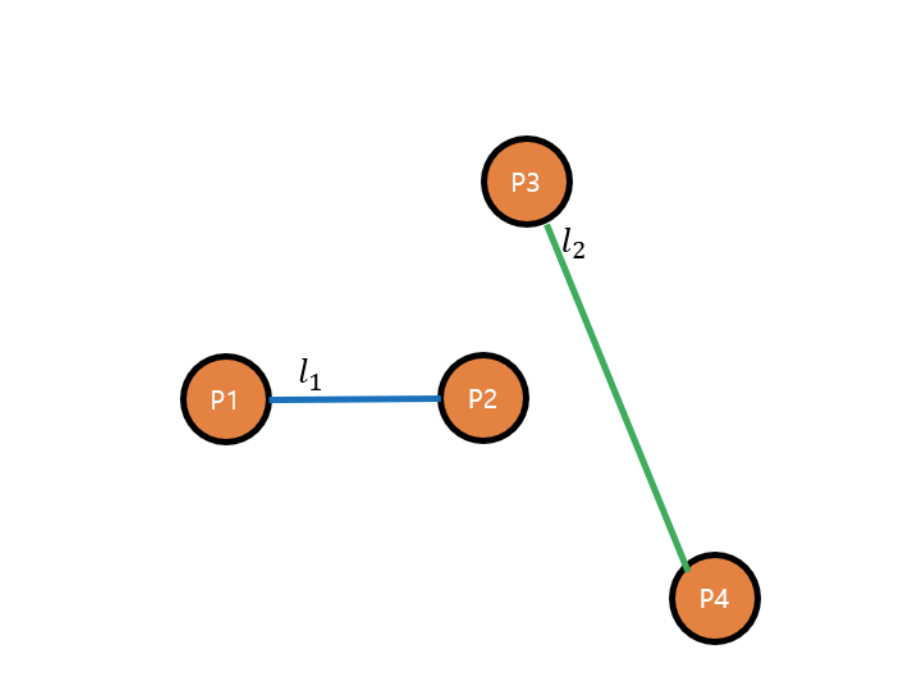
따라서 $ccw_{\vec{p3p4}}$ 인 ccw(p3,p4,p1) * ccw(p3,p4,p2) 또한 $\le0$ 임을 확인해야 선분 p1p2와 선분 p3p4가 교차한다는 것을 확신할 수 있다.
$ccw_{\vec{p3p4}} = ccw(p3,p4,p1) \times ccw(p3,p4,p2) \le 0$
즉, $ccw_{\vec{p1p2}} \le 0$ and $ccw_{\vec{p3p4}} \le 0$ 이어야 한다.

1-3. $ccw_{\vec{p1p2}} = 0$ and $ccw_{\vec{p3p4}} = 0$

하지만 $ccw_{\vec{p1p2}}$ 과 $ccw_{\vec{p3p4}}$ 둘 다 0일 때 반례가 생긴다. 두 선분이 일직선 상에 놓여있을 때다.

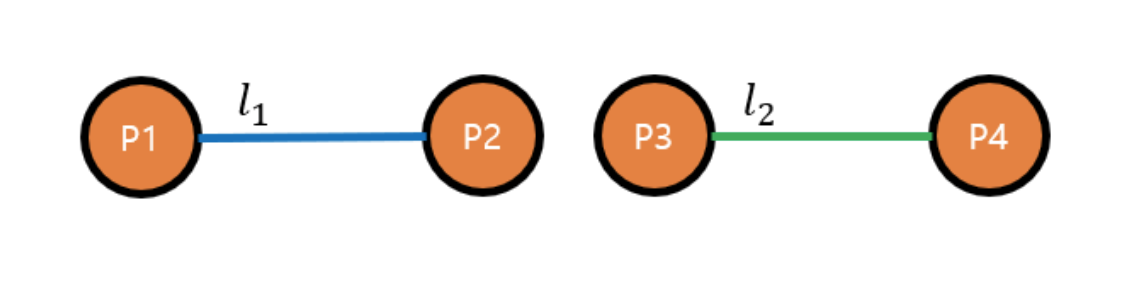
해당 경우 두 선분이

겹칠 수도 있고
끝점에서만 만날 수 있고
아예 안 만날 수도 있다.

이를 잘 생각해서 처리해 줘야 한다.

2. 교차점

두 선분의 교차점 (px,py)를 구하는 방정식은 사람마다 다른 것 같다. 하지만 나는 다음과 같은 공식을 사용했다.
해당 공식의 증명을 정리해 보았다. 혹시 궁금하다면 참고 바란다.
(참고: https://velog.io/@jinsoolve/선분-교차점-구하기-증명)

Vector p1p2 = p2-p1, p3p4 = p4-p3;

// p2.cross(p1): p2,p1의 외적
double px = p2.cross(p1)*p3p4.x - p1p2.x*p4.cross(p3);
double py = p2.cross(p1)*p3p4.y - p1p2.y*p4.cross(p3);
double p = p1p2.cross(p3p4);

px /= p; py /= p;

참고로 해당 공식을 사용할 때는 위에서 했던 것처럼 교차 여부를 확인했을 때만 사용할 것이다.
따라서 p == 0이 된다면 이는 p1p2와 p3p4가 일직선 위에 있다는 것을 의미한다.
p == 0 일 때 교차점을 출력해야 하는 부분은 끝점에서만 만날 때이므로 해당 부분을 잘 출력하고,
p != 0 이라면 바로 px,py를 출력해주면 된다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pll = pair<ll, ll>;
using ti3 = tuple<int, int, int>;

#define EPSILON 0.0001

struct Vector{
    double x, y;

    // constructor
    Vector() {}
    Vector(double _x, double _y) : x(_x), y(_y) {}

    // cross product
    double cross(const Vector &other) const {
        return x*other.y - y*other.x;
    }

    // operator overloading
    Vector operator -(Vector other) const {
        return Vector(x-other.x, y-other.y);
    }
    Vector operator *(Vector other) const {
        return Vector(x*other.x, y*other.y);
    }

    // compare overloading
    bool operator ==(Vector other) const {
        return (x == other.x) && (y == other.y);
    }
    bool operator <(Vector other) const {
        if(x == other.x) return y < other.y;
        return x < other.x;
    }
    bool operator <=(Vector other) const {
        return (*this == other) || (*this < other);
    }

    // print function
    void print() {
        cout << x << ' ' << y << '\n';
    }
};
double ccw(Vector a, Vector b, Vector c) {
    double res = (b-a).cross(c-b);
    if(res > EPSILON) return 1; // counter-clockwise
    if(res < -EPSILON) return -1; // clockwise
    return 0; // straight line
}
void findIntersectionPoint(Vector p1, Vector p2, Vector p3, Vector p4) {
    Vector p1p2 = p2-p1, p3p4 = p4-p3;
    double px = p2.cross(p1)*p3p4.x - p1p2.x*p4.cross(p3);
    double py = p2.cross(p1)*p3p4.y - p1p2.y*p4.cross(p3);
    double p = p1p2.cross(p3p4);

    if(fabs(p) < EPSILON) { // parallel
        if(p2 < p1) swap(p1,p2);
        if(p4 < p3) swap(p3,p4);
        if(p2 == p3) p2.print();
        else if(p4 == p1) p4.print();
    }
    else Vector(px/p, py/p).print(); // intersect
}
void solve(Vector p1, Vector p2, Vector p3, Vector p4) {
    double p1p2_ccw = ccw(p1,p2,p3) * ccw(p1,p2,p4);
    double p3p4_ccw = ccw(p3,p4,p1) * ccw(p3,p4,p2);

    // 1. parallel
    // 2. intersect at end point
    if(fabs(p1p2_ccw) < EPSILON && fabs(p3p4_ccw) < EPSILON) {
        if(p2 < p1) swap(p1, p2);
        if(p4 < p3) swap(p3,p4);

        if(p3 <= p2 && p1 <= p4) {
            cout << "1\n";
            findIntersectionPoint(p1,p2,p3,p4);
        }
        else cout << "0\n";
    }
    // just intersect normally
    else {
        if(p1p2_ccw < EPSILON && p3p4_ccw < EPSILON) {
            cout << "1\n";
            findIntersectionPoint(p1,p2,p3,p4);
        }
        else cout << "0\n";
    }
}

Vector p1, p2, p3, p4;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    cout << fixed; cout.precision(9);

    cin >> p1.x >> p1.y >> p2.x >> p2.y;
    cin >> p3.x >> p3.y >> p4.x >> p4.y;

    solve(p1,p2,p3,p4);

    return 0;
}

참고로 여기서는 0이라는 값 대신 -EPSILON ~ EPSILON 구간을 모두 0이라 생각하고 구현했다. double의 경우 완벽한 0이 안 될 수 있음을 감안해서 구현하였다. 사실 이 문제는 그런 걱정은 안 하고 그냥 0으로 해도 솔브 받을 수 있을 것이다.
(참고: https://bowbowbow.tistory.com/17#선분과-선분의-교차점)

김진수

https://jinsoolve.github.io으로 블로그 이전했습니다.

이전 포스트

2023.11.11. PS log

다음 포스트

2023.11.12. PS log

PS

P4 14868 문명

코드

후기

P4 10266 시계 사진들

코드

후기

P4 20149 선분 교차3

1. 교차여부

1-1. $ccw_{\vec{p1p2}}$

1-2. $ccw_{\vec{p3p4}}$

1-3. $ccw_{\vec{p1p2}} = 0$ and $ccw_{\vec{p3p4}} = 0$

2. 교차점

코드

2023.11.11. PS log

2023.11.13. PS log

0개의 댓글

2023.11.12. PS log

PS

P4 14868 문명

코드

후기

P4 10266 시계 사진들

코드

후기

P4 20149 선분 교차3

1. 교차여부

1-1. ccwp1p2⃗ccw_{\vec{p1p2}}ccwp1p2​​

1-2. ccwp3p4⃗ccw_{\vec{p3p4}}ccwp3p4​​

1-3. ccwp1p2⃗=0ccw_{\vec{p1p2}} = 0ccwp1p2​​=0 and ccwp3p4⃗=0ccw_{\vec{p3p4}} = 0ccwp3p4​​=0

2. 교차점

코드

2023.11.11. PS log

2023.11.13. PS log

0개의 댓글

1-1. $ccw_{\vec{p1p2}}$

1-2. $ccw_{\vec{p3p4}}$

1-3. $ccw_{\vec{p1p2}} = 0$ and $ccw_{\vec{p3p4}} = 0$