2023.11.13. PS log

김진수·2023년 11월 13일

boj-11868 boj-12899 boj-2261 boj-7469 구간합 님게임 머지소트 트리 분할정복 세그먼트 트리 펜윅트리 필승 전략 게임

PS

목록 보기

12/19

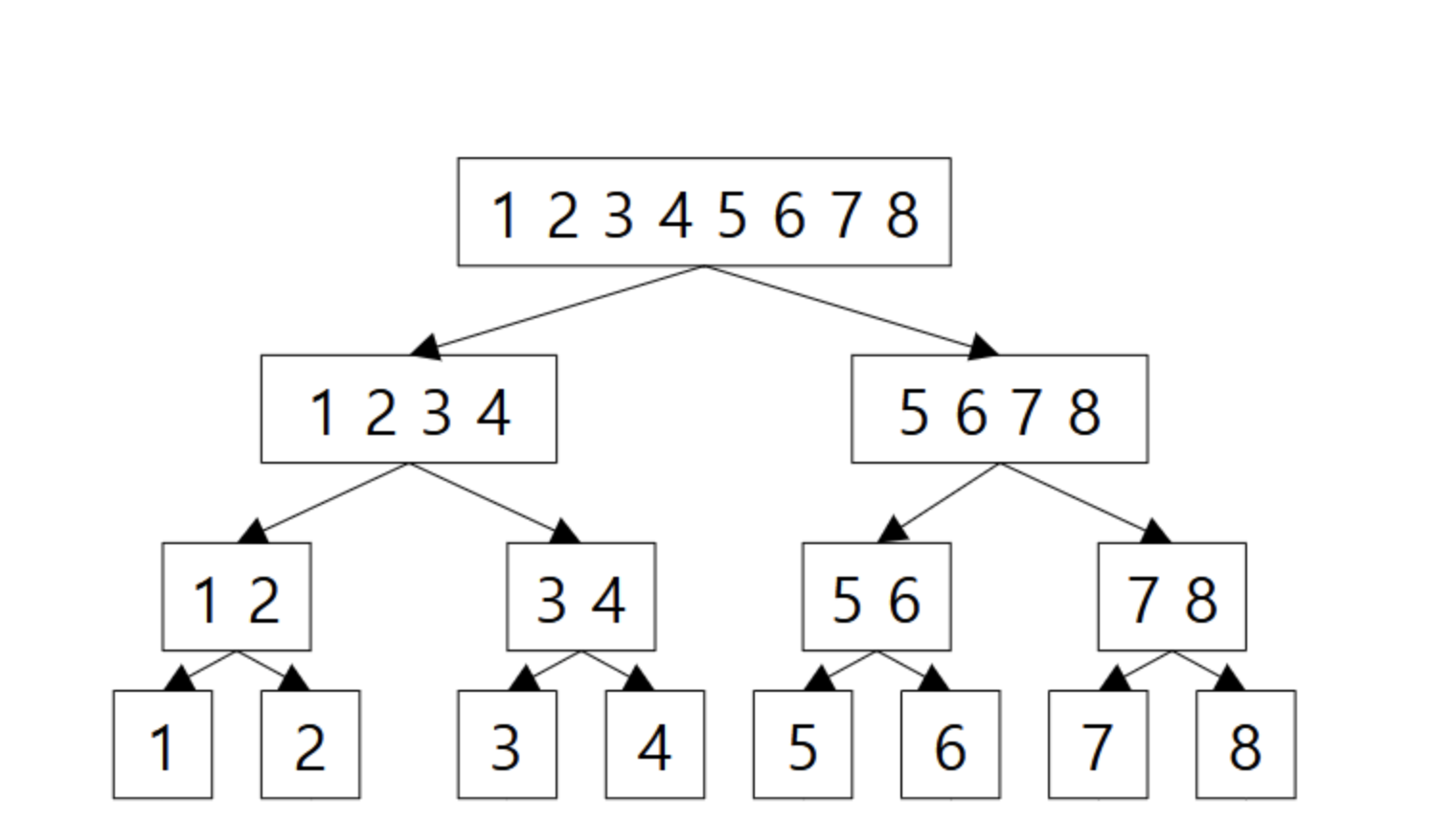
P4 12899 데이터 구조

12분 46초(세그먼트 트리) 18분 18초(펜윅트리)
보자마자 구간합이라는 것을 알았고 그냥 펜윅트리나 세그먼트 트리를 사용하면 간단히 풀린다.
시간은 동일하고 메모리는 확실히 펜윅트리가 유리하다.

코드 (세그먼트 트리)

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

const int MXN = 2e6;

class segment {
        public:
        vector<ll> tree; //tree[node] := a[start ~ end] 의 합

        segment() {}
        segment(int size) {
            this->resize(size);
        }
        void resize(int size) {
            size = (int) floor(log2(size)) + 2;
            size = pow(2, size);
            tree.resize(size);
        }
        ll sum(int node, int start, int end, int left, int right) {
            if(right < start || end < left) return 0;
            if(left <= start && end <= right) return tree[node];
            return sum(node * 2, start, (start + end) / 2, left, right) +
                   sum(node * 2 + 1, (start + end) / 2 + 1, end, left, right);
        }
        void update(int node, int start, int end, int index, ll diff) {
            if(index < start || end < index) return;
            tree[node] += diff;
            if(start != end) {
                update(node * 2, start, (start + end) / 2, index, diff);
                update(node * 2 + 1, (start + end) / 2 + 1, end, index, diff);
            }
        }
        int find(int node, int start, int end, int target) {
            if(start == end) return start;
            if(target <= tree[2*node]) return find(2*node, start, (start+end)/2, target);
            return find(2*node+1, (start+end)/2+1, end, target - tree[2*node]);
        }
};

int N;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> N;
    segment root(MXN);
    while(N--) {
        int t, x; cin >> t >> x;
        if(t == 1) root.update(1,1,MXN,x,1);
        else {
            int idx = root.find(1,1,MXN,x);
            cout << idx << '\n';
            root.update(1,1,MXN,idx,-1);
        }
    }


    return 0;
}

코드 (펜윅트리)

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

const int MXN = 2e6;

int N;
int fenwick[MXN+1];

int sum(int idx) {
    int ret = 0;
    while(idx) {
        ret += fenwick[idx];
        idx -= (idx & -idx);
    }
    return ret;
}
void update(int idx, int value) {
    while(idx <= MXN) {
        fenwick[idx] += value;
        idx += (idx & -idx);
    }
}
int find(int target) {
    int l=1, r=MXN, m;
    while(l < r) {
        m = (l+r) / 2;
        if(target <= sum(m)) r = m;
        else l = m+1;
    }
    return r;
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    memset(fenwick, 0, sizeof fenwick);

    cin >> N;
    while(N--) {
        int t,x; cin >> t >> x;
        if(t==1) update(x,1);
        else {
            int idx = find(x);
            cout << idx << '\n';
            update(idx, -1);
        }
    }


    return 0;
}

P4 11868 님게임2

1시간 4분 54초
필승 전략 게임으로 풀어야 한다.
(참고: https://librewiki.net/wiki/필승_전략_게임)

모든 돌더미들에 대해 xor을 한 값을 nim_sum이라 하자.
nim_sum == 0 이면, 후공이 승리하고
nim_sum != 0 이면, 선공이 승리한다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

int N;
vector<int> v;

int nim_sum(vector<int> &v) {
    int ret = 0;
    for(int x : v) {
        ret ^= x;
    }
    return ret;
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);


    cin >> N;
    for(int i=0; i<N; i++) {
        int x; cin >> x;
        v.emplace_back(x);
    }
    cout << (nim_sum(v) != 0 ? "koosaga" : "cubelover");

    return 0;
}

후기

필승전략게임을 알지 못하면 풀 수 없는 문제였다.

P4 2261

1시간 17분 38초
분할 정복은 바로 떠올렸으나, left, right를 어떻게 이어줄 지를 못 떠올렸다.
(참고: https://steady-coding.tistory.com/215)
dl = solve(l,m), dr = solve(m+1,r)을 구했다고 하자. d = min(dl,dr)
이때 내가 left상자와 right상자에서 점을 하나씩 골라 최솟값을 확인해야 한다.

이때 확인해야 하는 범위는 [m-d,m+d]이면 된다. 그 외에 범위는 어차피 d를 넘어가므로 의미가 없기 떄문이다.
해당 범위에 있는 점들을 y좌표로 정렬시킨후 p[i], p[i+1]의 거리를 구해 최솟값을 업데이트 시켜주면 끝이다.

y로 정렬시킨후 일일이 거리를 구해 최솟값 업데이트 시켜주는 과정은 선형 시간복잡도라 시간복잡도가 크지 않겠냐는 의문이 생길 수 있는데 저 영역에 있는 점은 많지 않다고 한다.
이유는 다음과 같다.

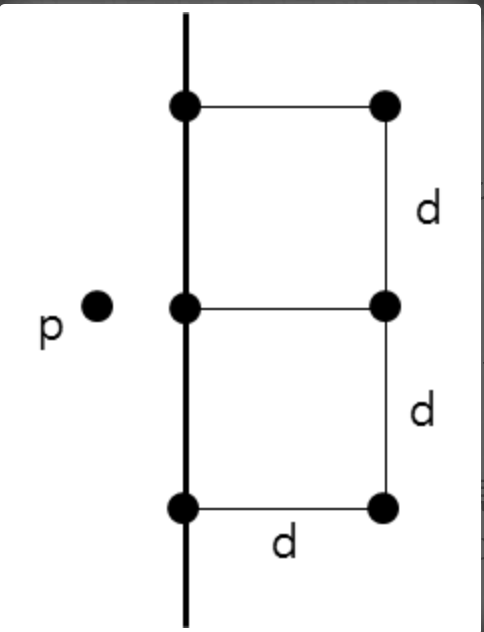
왼쪽 영역의 p에 대해서 오른쪽 영역의 점과 이어주려 할 때 다음과 같은 직사각형 안에만 점이 존재할 수 있다. d = min(dl,dr) 이므로 저 직사각형 안에는 점이 있을 수 없다. 따라서 최대 6개가 존재할 수 있으므로 개수는 절대 많지 않다고 한다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

const int mxn = 1e4;
int n;
vector<pii> points;

int root(int x) {
    return ceil(sqrt(x));
}
bool cmp(pii a, pii b) {
    if(a.y == b.y) return a.x < b.x;
    return a.y < b.y;
}
int dist2(pii p1, pii p2) {
    return (p2.x-p1.x)*(p2.x-p1.x) + (p2.y-p1.y)*(p2.y-p1.y);
}
int solve(int l, int r) {
    if(l > r) return INF;
    int m = (l+r)/2;
    int ret = INF;
    if(l != r) ret = min(ret, min(solve(l,m), solve(m+1, r)));
    l = max(l, m-root(ret)), r = min(r,m+root(ret));
    auto it1 = lower_bound(all(points), pii(l,0));
    auto it2 = upper_bound(all(points), pii(r,2*mxn));
    vector<pii> ysort(it1,it2);
    if(ysort.size() < 2) return ret;
    sort(all(ysort),cmp);
    for(int i=0; i<ysort.size()-1; i++) {
        ret = min(ret, dist2(ysort[i], ysort[i+1]));
    }
    return ret;
}

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n;
    points.resize(n);
    for(int i=0; i<n; i++) {
        cin >> points[i].x >> points[i].y;
        points[i].x += mxn;
        points[i].y += mxn;
    }
    sort(all(points));
    cout << solve(0,2*mxn) << '\n';

    return 0;
}

P2 7469 K번째 수

26분 39초
머지소트 트리를 알아야 풀 수 있는 문제다.
query를 수행할 때 이분탐색을 해서 푼다.
-1e9 ~ 1e9 사이를 이분 탐색해서 i ~ j 사이에서 x값보다 작거나 같은 값이 몇개인지 확인한다. 시간복잡도는 다음과 같다.
(호출된 수) x (x를 찾기 위한 이분탐색) x (트리 탐색) x (배열에 대한 이분탐색)

m \times log_2{2e9} \times log_2N \times log_2N \approx 4\times 10^7

머지소트 트리란?
머지소트 하는 과정을 트리에 저장한 것이다.

코드

#include <iostream>
#include <algorithm>
#include <cmath>
#include <utility>
#include <string>
#include <cstring>
#include <vector>
#include <tuple>
#include <stack>
#include <queue>
#include <deque>
#include <list>
#include <map>
#include <unordered_map>
#include <climits>

#define INF 987654321
#define INF2 2147483647
#define f first
#define s second
#define x first
#define y second
#define all(v) (v).begin(), (v).end()

using namespace std;
using ll = long long;
using pii = pair<int, int>;
using ti3 = tuple<int, int, int>;

class segment {
public:
    vector<vector<int>> tree; //tree[node] := a[start ~ end] 의 합

    segment() {}
    segment(int size) {
        this->resize(size);
    }
    void resize(int size) {
        size = (int) floor(log2(size)) + 2;
        size = pow(2, size);
        tree.resize(size);
    }
    void update(int node, int start, int end, int idx, int value) {
        if(idx < start || end < idx) return;
        tree[node].emplace_back(value);
        if(start != end) {
            update(2*node, start, (start+end)/2, idx, value);
            update(2*node+1, (start+end)/2+1, end, idx, value);
        }
    }
    int query(int node, int start, int end, int left, int right, int x) {
        if(right < start || end < left) return 0;
        if(left <= start && end <= right) return upper_bound(all(tree[node]), x) - tree[node].begin();
        return query(2*node, start, (start+end)/2, left, right, x) + query(2*node+1, (start+end)/2+1, end, left, right, x);
    }
};

int n, m;
vector<int> v;
unordered_map<int,int> Idx;

int main(void) {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    cin >> n >> m;
    v.resize(n);
    for(int i=0; i<n; i++) {
        cin >> v[i];
        Idx[v[i]] = i+1;
    }

    sort(all(v));
    segment root(n);
    for(int x : v) {
        root.update(1,1,n,Idx[x], x);
    }

    while(m--) {
        int i, j, k; cin >> i >> j >> k;
        int l = -1e9, r = 1e9, m;
        while(l <= r) {
            m = (l+r)/2;
            int res = root.query(1,1,n,i,j,m);
            if(res < k) l = m+1;
            else r = m-1;
        }
        cout << l << '\n';
    }


    return 0;
}