
Session Review
공분산 - 상관계수
분산과 공분산의 차이?
분산이 하나의 데이터가 얼마나 퍼져있는지를 나타내는 기술통계치라면, 공분산은 두 개의 데이터에 대한 분산을 비교해서 연관성을 파악하는 것
공분산
1개의 변수(x) 값이 변화할 때, 다른 변수(y)가 어떠한 연관성을 나타내며 변하는지 측정하는 것
- cov(x,y) < 0: x가 커지면 y는 작아짐 = 음의 공분산 값
- cov(x,y) > 0: x가 커지면 y도 커짐 = 양의 공분산 값
- cov(x,y) ~ 0: x와 y의 관련성을 알 수 없음 = 0에 가까운 공분산 값
-> 큰 값의 공분산은 두 변수간의 큰 연관성을 나타냄
👀 변수들이 다른 스케일을 가지고 있다면 실제 변수의 연관성과 관련 없이 영향을 받게 됨
e.g. 두 변수가 연관성이 적더라도 큰 스케일을 가지고 있다면, 연관이 높지만 스케일이 작은 변수들에 비해 높은 공분산 값 가짐
상관계수
공분산의 스케일을 보정하기 위한 것 = 평준화
상관계수 cor(x,y) = 공분산 / 두 변수의 표준편차
정해진 범위가 없는 공분산과 달리 상관계수는 -1에서 1까지로 정해진 범위 안의 값만을 가지며, 선형연관성이 없는 경우 0에 근접한 값이 나옴
일반적으로 상관계수의 절대값이 0.3보다 작으면 연관성이 약한 관계로, 0.7보다 크면 연관성이 강한 관계로 해석
- cor(X, Y) > 0: X가 증가 할 때 Y도 증가한다.(양의 상관관계)
- cor(X, Y) < 0: X가 증가 할 때 Y는 감소한다.(음의 상관관계)
- cor(X, Y) = 0: 상관계수가 0이라면 두 변수간에는 아무런 선형관계가 없음
- cor(X, Y) = 1: X와 Y가 동일한 값을 가진다.
- cor(X, Y) = -1: X와 Y가 반대 방향으로 동일한 값을 가진다.
상관계수가 공분산보다 더 좋은 지표로 사용되는 이유
- 공분산은 이론상 모든 값을 가질 수 있으나, 상관계수는 -1 ~ 1 사이로 정해져 비교하기 쉽다
- 공분산은 항상 스케일, 단위를 포함하고 있으나, 상관계수는 이에 영향을 받지 않는다
- 상관계수는 데이터의 평균 or 분산의 크기에 영향을 받지 않는다
벡터의 직교(orthogonality)
두 벡터의 내적값이 0이라면 이 두 벡터는 직교(서로 수직으로 배치)
👀 좌표상에 있는 거의 모든 벡터는 다른 벡터와 상관이 아주 작게라도 있으나, 유일하게 수직인 벡터만 상관 관계가 전혀 없다! (하나의 벡터가 증가할 때, 다른 벡터는 이에 영향을 받지 않는다)
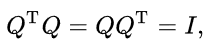
위와 같은 조건을 만족하는 Q는 직교 행렬
단위벡터
벡터를 표현할 때 기본단위가 되는 벡터 (단위길이(1)을 갖는 벡터)
👀 벡터들은 단위벡터의 조합단위벡터 * scalar으로 표현이 가능하다
1,2,3차원의 단위벡터
unit vector:
unit vectors: ,
unit vectors: , ,
span
벡터의 조합(linear combination)으로 만들 수 있는 벡터의 집합 (벡터 1개로도 가능: 길이 조절 정도)
= 선형독립관계에 있는 벡터들로 만들 수 있는 공간
e.g. 두 벡터가 같은 선상에 있는 경우, 벡터들은 선형 종속 관계에 있다고 표현 -> 선 외부의 새로운 벡터 생성 불가 => 두 벡터가 존재함에도 불구하고, 이러한 벡터의 span은 평면 공간이 아닌, 벡터가 이미 올려져있는 선으로 제한
e.g.2. 같은 선상에 있지 않는 벡터들은 선형 독립 관계에 있다고 표현 -> 주어진 공간 (2개의 벡터의 경우 평면)의 모든 벡터를 조합을 통해 만들어낼 수 있음
basis
어떤 벡터공간 V의 벡터들이 선형독립이면서 벡터공간 V 전체를 생성할 수 있다면, 이 벡터들의 집합을 의미
인 벡터공간을 표현하기 위해 필요한 최소한의 벡터들의 모음
👀 span의 역개념 = span의 재료가 되는 벡터
e.g. 인 벡터공간의 경우 최소한 필요한 벡터는 3개
rank
rank : 임의의 행렬 A에서 이 행렬의 열들로 생성될 수 있는 벡터공간의 차원
= 행렬의 열들 중에서 선형 독립인 열들의 최대 개수
= 행에 대해 나타내어 지는 공간의 차원
👀 column rank = row rank = full rank (행 기준 rank나 열 기준 rank 값은 같음)
span과 rank
span은 선형독립관계에 있는 벡터들로 만들 수 있는 공간
rank는 span을 시각화할 수 있는 차원이 몇 차원인지 보여줌
Gaussian elemination
rank를 확인하는 방법 중 하나
Gaussian Elimination 은 주어진 매트릭스를 "Row-Echelon form"으로 바꾸는 계산과정
👀 연립방정식을 matrix로 만들었을 때 계산하는 방법과 유사
linear projection
vector projection은 두 개의 벡터 중 하나를 다른 하나에 투영(projection)시키는 것 = 하나의 벡터를 다른 벡터로 옮겨서 표현하는 것 (like 그림자)
👀 왜 필요할까?
의미가 작은 feature(column)들은 제거하면서 원래 데이터가 가지고 있는 insight는 충분히 제공할 수 있는 방법이기 때문 -> 차원 축소의 근본이 되는 기술
Food for Thought
선형조합(선형종속, 선형독립)
- https://twlab.tistory.com/24
- https://blog.naver.com/PostView.naver?blogId=sw4r&logNo=221949338397&parentCategoryNo=&categoryNo=198&viewDate=&isShowPopularPosts=false&from=postView
- 선형결합이 0이 되는 상수 값이 0밖에 없을 때, 선형 독립
❓ '연관이 없는 것'과 '독립적인 것'은 어떤 차이일까?
직교 관계인 벡터들은 기저 벡터가 될 수 있을까?
❗️ 벡터공간 - span
선형관계에 있는 벡터는 데이터 분석에서 어떤 의미?
동일한 데이터인데 단위 또는 스케일만 다른 것
e.g. [1m, 2m] = [2ft, 4ft]
-> 데이터의 퀄리티가 구리다…를 보여줌
-> 데이터 분석 방법을 바꾸거나, 데이터를 재수집하는 방법이 있음
