1월 7일 - 반 나누기 [BOJ/31397]

문제 설명

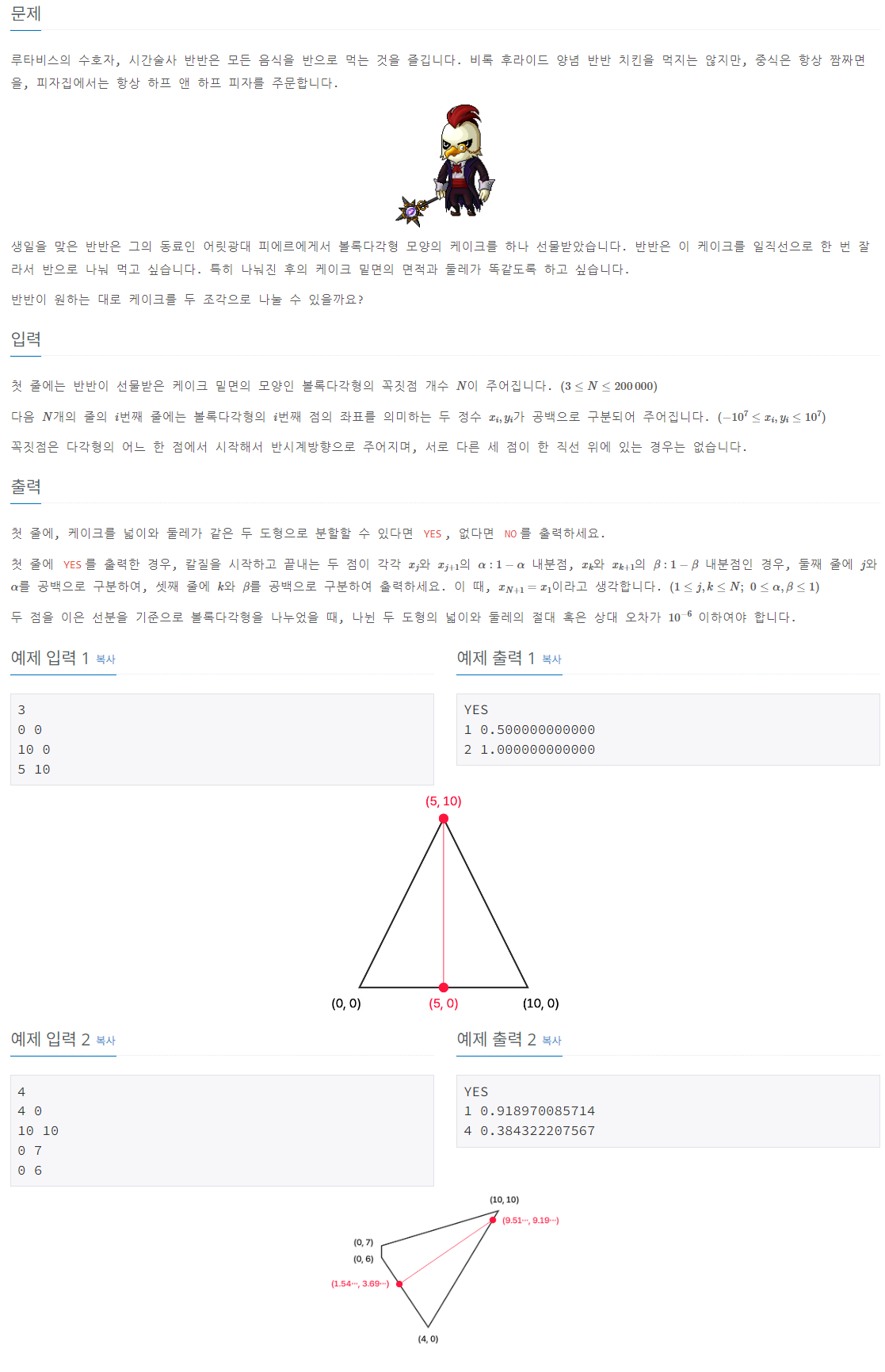
반반은 볼록다각형 모양의 케이크를 선물받았다. 그는 이 케이크를 한 번의 직선으로 나누어, 나눠진 두 도형의 넓이와 둘레가 정확히 같도록 하고 싶다.
이 문제에서 우리는 다각형의 좌표가 주어졌을 때, 위 조건을 만족하는 분할점과 그 결과를 계산해야 한다.

접근 방식

1. 기본 정의:

   • 주어진 다각형은 반시계 방향으로 주어진다.
   • 둘레와 넓이를 계산하여, 나눠진 두 영역이 같은 둘레와 넓이를 가지도록 분할점을 찾아야 한다.

2. 전처리:

   • 모든 변의 길이를 계산하고 누적 길이를 저장하여 둘레(perimeter)를 빠르게 계산.
   • 다각형의 넓이를 계산하기 위해 슈메이커 공식을 적용.

3. 분할 점 탐색:

   • 이분 탐색을 활용하여 분할 지점을 둘레의 절반 위치에서 찾아간다.
   • 분할 지점과 관련된 좌표를 계산하여 해당 면적을 확인한다.

4. 결과 출력:

   • 이분 탐색 결과를 기반으로, 분할을 시작하고 끝내는 지점의 좌표를 계산하고 출력한다.

코드

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

// 입력 데이터 및 계산을 위한 변수들
int vertexCount;  // 다각형의 꼭짓점 개수
pair<ll, ll> vertices[200001];  // 꼭짓점 좌표 저장

double perimeter, totalArea;  // 다각형 둘레와 전체 면적

double cumulativeLength[200001];  // 각 변까지의 누적 길이

// 두 점 사이의 거리 계산 함수
double calculateDistance(int p1, int p2) {
    double dx = vertices[p1].first - vertices[p2].first;
    double dy = vertices[p1].second - vertices[p2].second;
    return sqrt(dx * dx + dy * dy);
}

// 특정 선분으로 다각형을 나누었을 때 면적 비교 함수
bool isLargerArea(double startSegment) {
    double endSegment = perimeter / 2.0 + startSegment;

    // 시작점 좌표 계산
    int startIdx = upper_bound(cumulativeLength, cumulativeLength + vertexCount + 1, startSegment) - cumulativeLength;
    if (startIdx == vertexCount + 1) {
        startSegment -= perimeter;
        startSegment = abs(startSegment);
        startIdx = 1;
    }
    startSegment -= cumulativeLength[startIdx - 1];
    double ratioStart = startSegment / calculateDistance(startIdx - 1, startIdx);
    pair<double, double> startPoint = {
        vertices[startIdx - 1].first * (1.0 - ratioStart) + vertices[startIdx].first * ratioStart,
        vertices[startIdx - 1].second * (1.0 - ratioStart) + vertices[startIdx].second * ratioStart
    };

    // 끝점 좌표 계산
    int endIdx = upper_bound(cumulativeLength, cumulativeLength + vertexCount + 1, endSegment) - cumulativeLength;
    if (endIdx == vertexCount + 1) {
        endSegment -= perimeter;
        endSegment = abs(endSegment);
        endIdx = 1;
    }
    endSegment -= cumulativeLength[endIdx - 1];
    double ratioEnd = endSegment / calculateDistance(endIdx - 1, endIdx);
    pair<double, double> endPoint = {
        vertices[endIdx - 1].first * (1.0 - ratioEnd) + vertices[endIdx].first * ratioEnd,
        vertices[endIdx - 1].second * (1.0 - ratioEnd) + vertices[endIdx].second * ratioEnd
    };

    // 나눈 영역의 면적 계산
    vector<pair<double, double>> splitVertices;
    splitVertices.push_back(startPoint);

    startIdx %= vertexCount;
    endIdx %= vertexCount;
    int idx = startIdx;

    while (true) {
        if (idx == endIdx) break;
        splitVertices.push_back(vertices[idx]);
        ++idx;
        idx %= vertexCount;
    }
    splitVertices.push_back(endPoint);
    splitVertices.push_back(startPoint);

    double splitArea = 0.0;
    for (int i = 0; i + 1 < splitVertices.size(); ++i) {
        splitArea += splitVertices[i].first * splitVertices[i + 1].second;
        splitArea -= splitVertices[i].second * splitVertices[i + 1].first;
    }
    splitArea = abs(splitArea) / 2.0;

    return splitArea > totalArea / 2.0;
}

void solve() {
    // 입력 처리
    cin >> vertexCount;
    for (int i = 0; i < vertexCount; ++i) {
        cin >> vertices[i].first >> vertices[i].second;
    }
    vertices[vertexCount] = vertices[0];  // 다각형 닫기

    // 각 변의 길이를 누적 계산
    cumulativeLength[0] = 0.0;
    for (int i = 0; i < vertexCount; ++i) {
        int nextIdx = i + 1;
        cumulativeLength[nextIdx] = cumulativeLength[i] + calculateDistance(i, nextIdx);
    }
    perimeter = cumulativeLength[vertexCount];

    // 다각형의 전체 면적 계산
    for (int i = 0; i < vertexCount; ++i) {
        totalArea += vertices[i].first * vertices[i + 1].second;
        totalArea -= vertices[i].second * vertices[i + 1].first;
    }
    totalArea = abs(totalArea) / 2.0;

    // 이분 탐색으로 적절한 분할점 찾기
    double left = 0.0, right = perimeter / 2.0;
    int leftResult = isLargerArea(left), rightResult = isLargerArea(right);

    if (leftResult == rightResult) leftResult = 1 - leftResult;

    for (int i = 0; i < 100; ++i) {
        double mid = (left + right) / 2.0;
        int midResult = isLargerArea(mid);
        if (midResult == leftResult) {
            left = mid;
        } else {
            right = mid;
        }
    }

    // 결과 출력
    double splitStart = (left + right) / 2.0;
    double splitEnd = perimeter / 2.0 + splitStart;

    int startIdx = upper_bound(cumulativeLength, cumulativeLength + vertexCount + 1, splitStart) - cumulativeLength;
    if (startIdx == vertexCount + 1) {
        splitStart -= perimeter;
        splitStart = abs(splitStart);
        startIdx = 1;
    }
    splitStart -= cumulativeLength[startIdx - 1];
    double startRatio = splitStart / calculateDistance(startIdx - 1, startIdx);

    cout << "YES\n";
    cout << startIdx << ' ' << fixed << setprecision(12) << startRatio << '\n';

    int endIdx = upper_bound(cumulativeLength, cumulativeLength + vertexCount + 1, splitEnd) - cumulativeLength;
    if (endIdx == vertexCount + 1) {
        splitEnd -= perimeter;
        splitEnd = abs(splitEnd);
        endIdx = 1;
    }
    splitEnd -= cumulativeLength[endIdx - 1];
    double endRatio = splitEnd / calculateDistance(endIdx - 1, endIdx);

    cout << endIdx << ' ' << fixed << setprecision(12) << endRatio << '\n';
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    solve();
}

과정 설명

1. 입력 처리:

   • (N)개의 정점을 입력받아 배열 vertices에 저장.
   • 주어진 다각형을 닫기 위해 첫 번째 점을 마지막 점으로 복사.

2. 누적 길이 계산:

   • cumulativeLength 배열에 각 변까지의 누적 길이를 저장해 나중에 빠르게 참조.

3. 넓이 계산:

   • 슈메이커 공식을 사용해 다각형의 넓이를 계산.

4. 이분 탐색:

   • 나눌 지점을 탐색하며, 나눈 영역의 면적이 전체의 절반인지 확인.

5. 결과 출력:

   • 분할 지점 좌표를 계산해 출력.

So...

이 문제는 다각형의 기하학적 성질과 이분 탐색의 조합을 활용한 문제였다. 처음에는 복잡해 보였지만, 기하학적 계산을 정리하고 이분 탐색으로 분할점을 찾는 과정에서 효율적인 해결책을 도출할 수 있었다. 이번 풀이로 기하학적 최적화 문제에 대한 감각을 기를 수 있었다.