[Information Retrieval] 3. Dictionaries and tolerant retrieval

hoho·2024년 4월 17일
0

Information Retrieval

목록 보기
4/6

http://cislmu.org 와 학교 수업을 토대로 정리합니다.

1. Recap

Type/token distinction

  • Token: 문서에서 나타나는 실제 word/term의 인스턴스.
  • Type: 토큰들의 equivalence class

ex) In June, the dog likes to chase the cat in the barn

  • token: 12개 (, 제거)
  • word type: 9개

Problems in tokenization

delimiters? Space? Apostrophe? Hyphen? 이런 것들은 어떻게 처리할 것인가?
어떨 때는 구분자일 때도 있지만, 어떨 때는 아닐 수도 있기 때문에 애매하다.
거기다가 비영어권으로 확장하면 중국어, 일본어처럼 공백이 없고, 한술 더 떠 공백도 없는데 합성어가 있는 언어도 많다.

Problems with equivalence classing

term은 token들의 equivalence class이다.
그럼 equivalence class들은 어떻게 정의할 수 있을까?

  • Numbers (3/20/91 vs 20/3/91)
  • Case folding
  • Stemming, Porter stemmer
  • Morphological analysis: inflectional vs derivational
  • 타 언어 고려(Accent, umlauts, 변형 등 - 핀란드어는 단어 하나에 12000개의 다른 형태가 존재할 수 있다고 한다)

Skip pointers

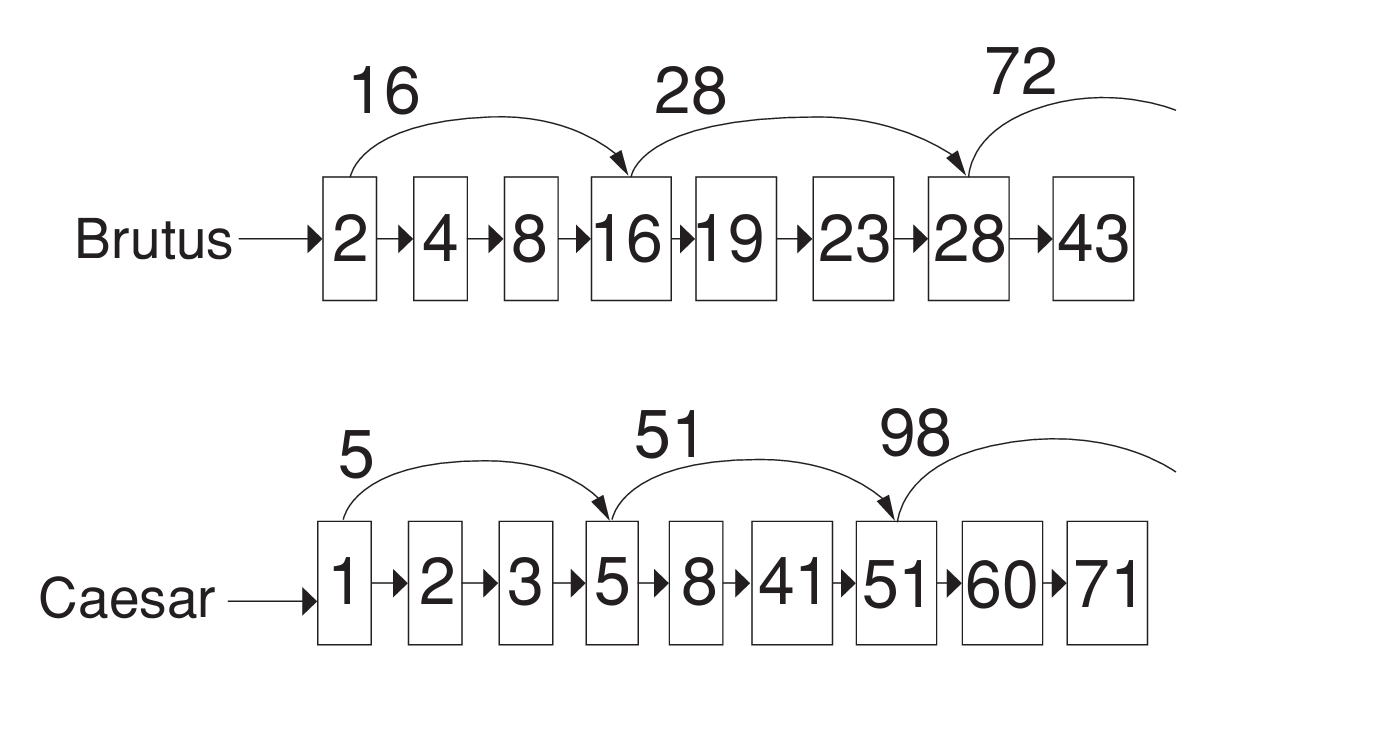
더 빠른 서치를 위해 Skip을 사용한다.
skip을 두는 위치는 skip의 빈도와 skip할 양을 trade-off해서 조절한다고 배운 바 있다.

Positional indexes

Positional index에 대해 2장에서 배운 바 있다.

이러한 Positional indexes를 가지고, 우리는 phrase queries, proximity queries 두 가지에 대해 답변할 수 있다.

Take-away

3장에서는 아래와 같은 내용들을 다룬다.

  • Tolerant retrieval: 쿼리 term과 문서 term 간에 정확히 매치되는 게 없을 땐 어떻게 해야 할까?
  • Wildcard queries
  • Spelling correction

2. Dictionaries

Inverted index

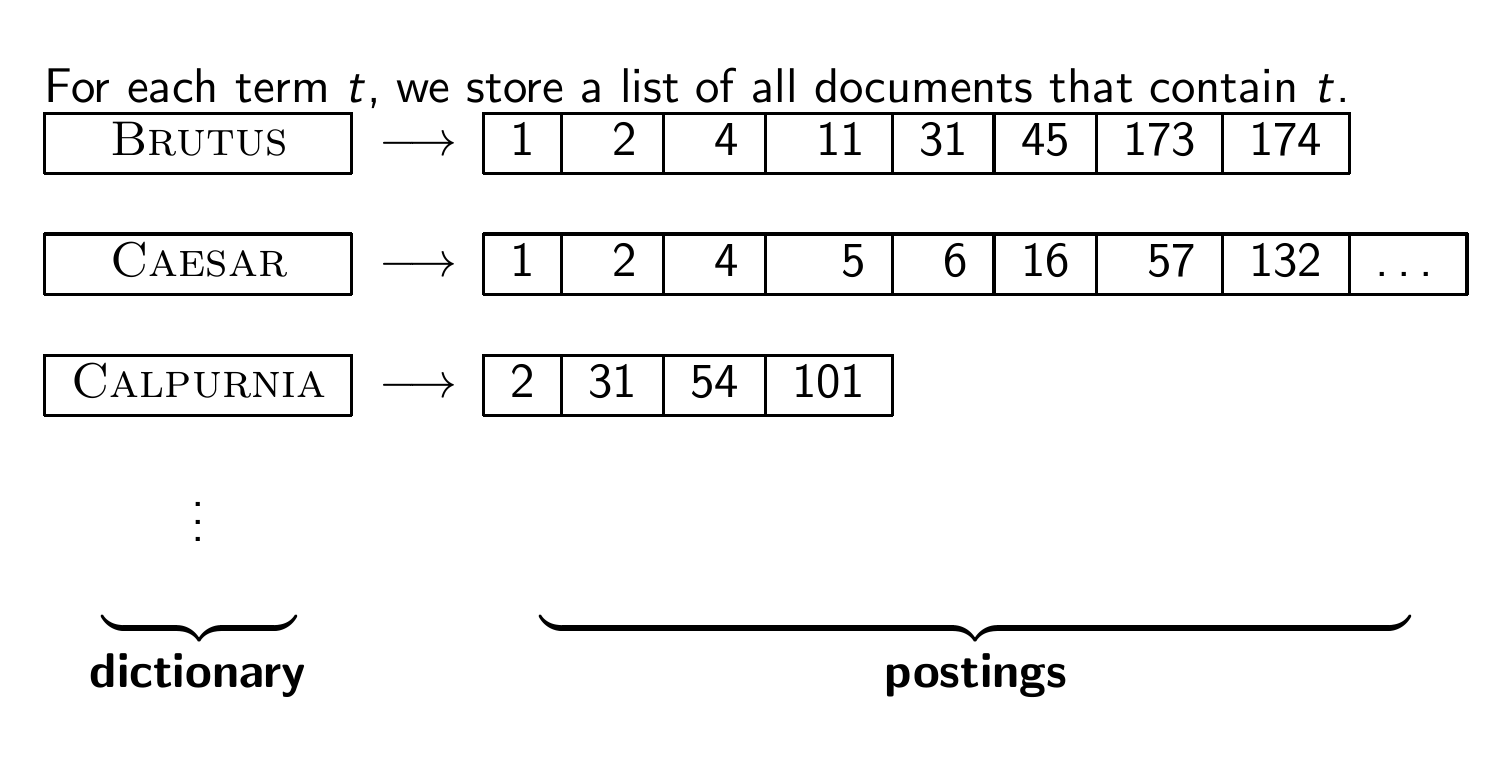
1장에서 Inverted index가 뭔지 배웠었다.

Dictionaries

딕셔너리는 term vocabulary를 저장하는 자료 구조이다.

term vocabulary는 데이터고,
dictionary는 term vocabulary를 저장하는 자료구조임을 유념하자.

Dictionary as array of fixed-width entries

각각의 term에 대해 몇 가지 것들을 저장해야 한다.

  • document frequency
  • pointer to postings list
  • 다 앞에서 배웠던 내용들이다.

우리가 이런 정보를 fixed-length entry 안에 배열로 저장한다고 가정하자.

이렇게 엄청나게 긴 배열 내에서 특정 용어를 어떻게 빠르게 찾을 수 있을까? -> 트리와 해시라는 선택지가 있다. (아래 참고)

Data structures for looking up term

해시와 트리의 2가지 선택지가 있다고 했다.
둘 중 무엇을 써야 하는지는 어떻게 정하는 걸까?

기준:

  • 항목 수의 고정 여부 (term 개수가 계속 늘어나는가? -> 변동이 크다면 트리가 좋음)
  • 다양한 키가 접근될 상대적 빈도수 (어떤 키가 자주 접근되는가? -> 균일하게 접근된다면 해시가 좋음)
  • 예상되는 term 수

해시는 상수 시간(O(1))이 걸리고, 트리는 로그 시간(O(log n))이 걸린다고 한다.

Hashes

각각의 vocabulary term은 정수로 해싱되며, 그 정수가 배열에서의 행 번호가 된다.
즉 쿼리가 시작되면 query term을 해싱하고, 고정 너비 배열에서 항목을 찾는다.

  • 장점: 해시를 통한 조회 속도가 매우 빠르다.
  • 단점:
    • 소규모 변이를 찾을 수 없음 (예를 들어 resume와 résumé를 구별할 수 없다. 해시 함수는 정확히 일치하는 키에 대해서만 값을 찾을 수 있기 때문이다)
    • prefix(접두사) 검색 불가능: 특정 접두사로 시작하는 용어 검색 불가
    • term 수가 계속 증가할 경우 재해시 필요

Trees

Tree는 prefix 문제를 해결할 수 있다. 이는 트리가 정렬된 순서로 데이터를 저장하므로, 범위 검색이나 순차 검색이 가능하기 때문이다.

다만 해시와 대비하여 검색 속도가 약간 느리다.
O(log M) => M은 vocabulary의 크기
그런데 위 시간복잡도는 트리가 균형 잡힌 경우에만 유효하며, 트리가 균형을 잃으면 검색 성능이 저하된다.

이진 트리의 균형을 잡는 것은 비용이 많이 든다.

=> B-tree를 이용해 균형 문제를 해결할 수 있다.

Binary tree

Tree의 가장 간단한 구조이다.

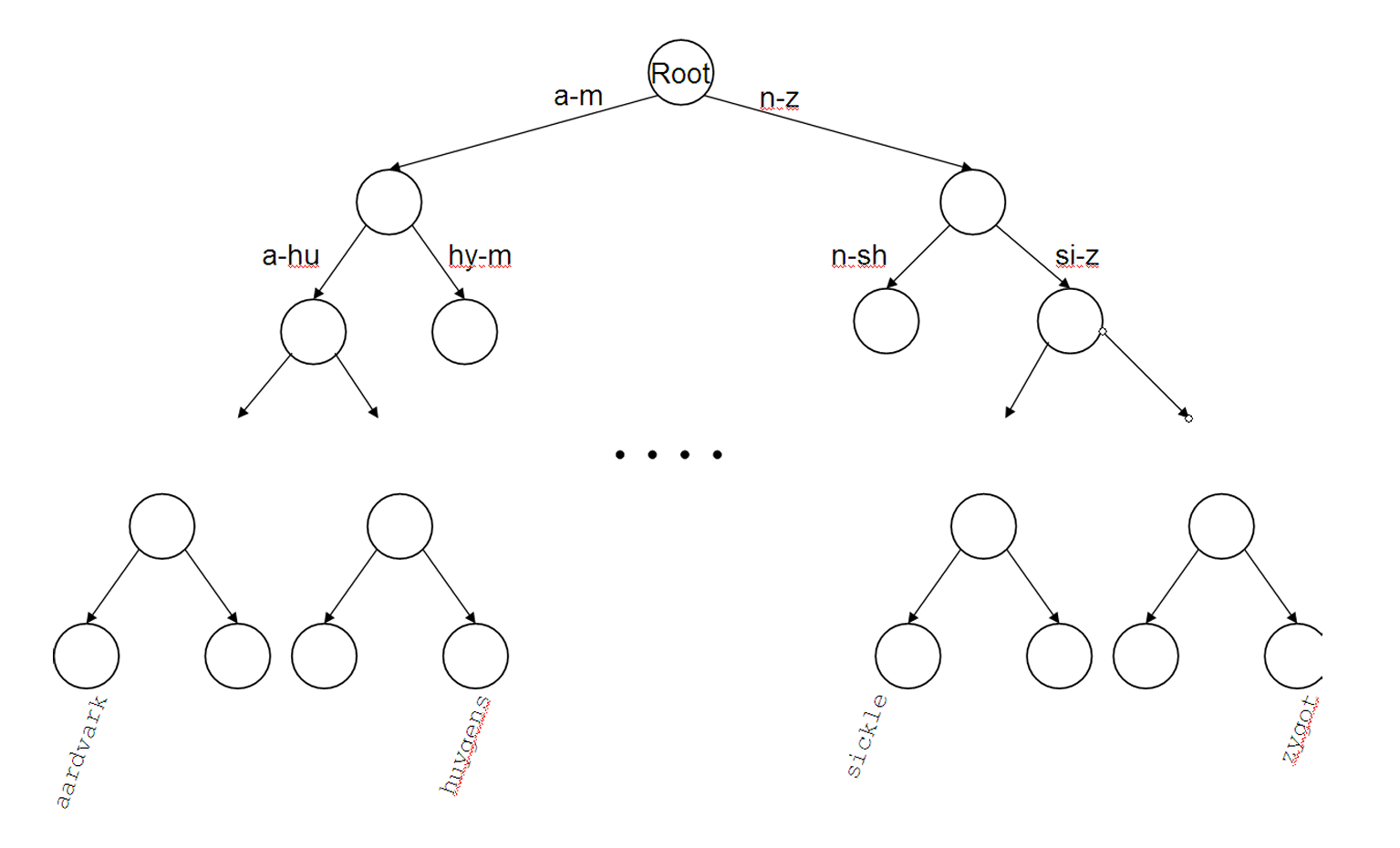
B-tree

B-트리는 각 내부 노드가 일정 범위[a, b]의 자식 수를 가지도록 설계된다. 효율적이라서 데이터베이스 시스템이나 파일 시스템에서 널리 사용된다.

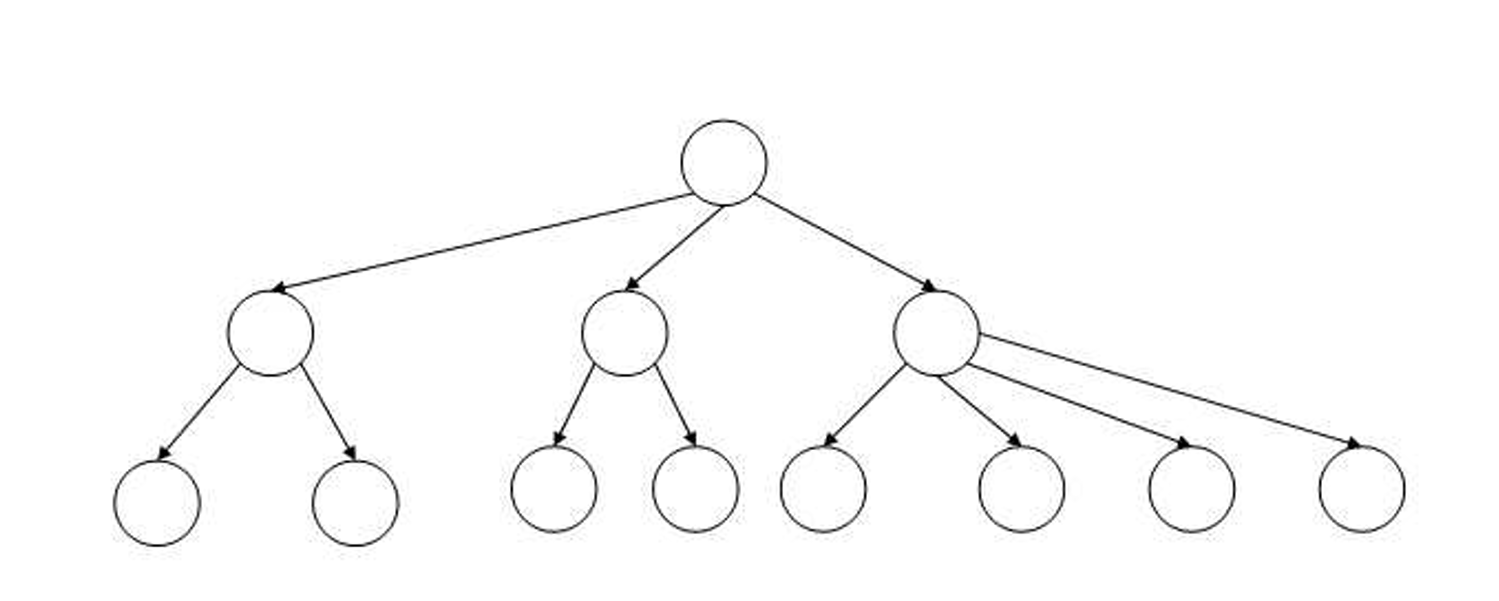
범위가 [2, 4]인 B-tree의 예시이다.

3. Wildcard queries

Wildcard queries

와일드카드란?
-> 텍스트 값에서 알 수 없는 문자를 사용할 수 있는 특수 문자로, 철자가 정확히 기억나지 않을 때 와일드카드 문자를 사용해 특정 항목을 찾을 수 있다. (참고: https://support.microsoft.com/ko-kr/topic/%EC%99%80%EC%9D%BC%EB%93%9C%EC%B9%B4%EB%93%9C-%EB%AC%B8%EC%9E%90%EC%9D%98-%EC%98%88-939e153f-bd30-47e4-a763-61897c87b3f4)

예를 들어,
mon*
은 mon으로 시작하는 모든 term을 포함하는 문서를 찾는다.
B-tree 딕셔너리를 사용하면 쉽게 처리할 수 있는데, mon으로 시작하고 moo로 시작하는 단어 사이에 있는 모든 용어들을 범위 검색하여 찾을 수 있다.

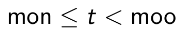
*mon
d은 mon으로 끝나는 모든 term을 포함하는 문서를 찾는다.
이를 위해 트리를 역순으로 한 개 더 유지하는 것이 필요하다.
정확히는, 역순으로 해놓은 후 nom으로 시작하고 non으로 시작하는 단어 사이에 있는 모든 용어들을 범위 검색한다.

최종 결과로는 와일드카드 쿼리에 해당하는 모든 용어들이 매칭되며, 그 다음 해당 용어를 포함하는 모든 문서를 검색하게 된다.

How to handle * in the middle of a term

*가 중간에 있으면 어떻게 될까?

m*nchen
이라는 쿼리가 있다고 하면, B-tree에서 m와 nchen을 찾은 후 교집합해야한다.
당연히 비용이 크다.
그래서 permuterm index라는 대안이 나왔다.

Permuterm index

permuterm index의 기본 아이디어는 모든 와일드카드 쿼리를 회전하여 마지막에 *가 나오도록 하는 것이다.
이러한 각 회전을 B-tree 딕셔너리에 저장한다.

회전이 무슨 말인가 싶을 것이다.
예를 들어 HELLO가 있다고 하면

hello$, ello$h, llo$he, lo$hel, o$hell, $hello

위 내용들을 B-tree에 저장한다.

Permuterm -> term mapping

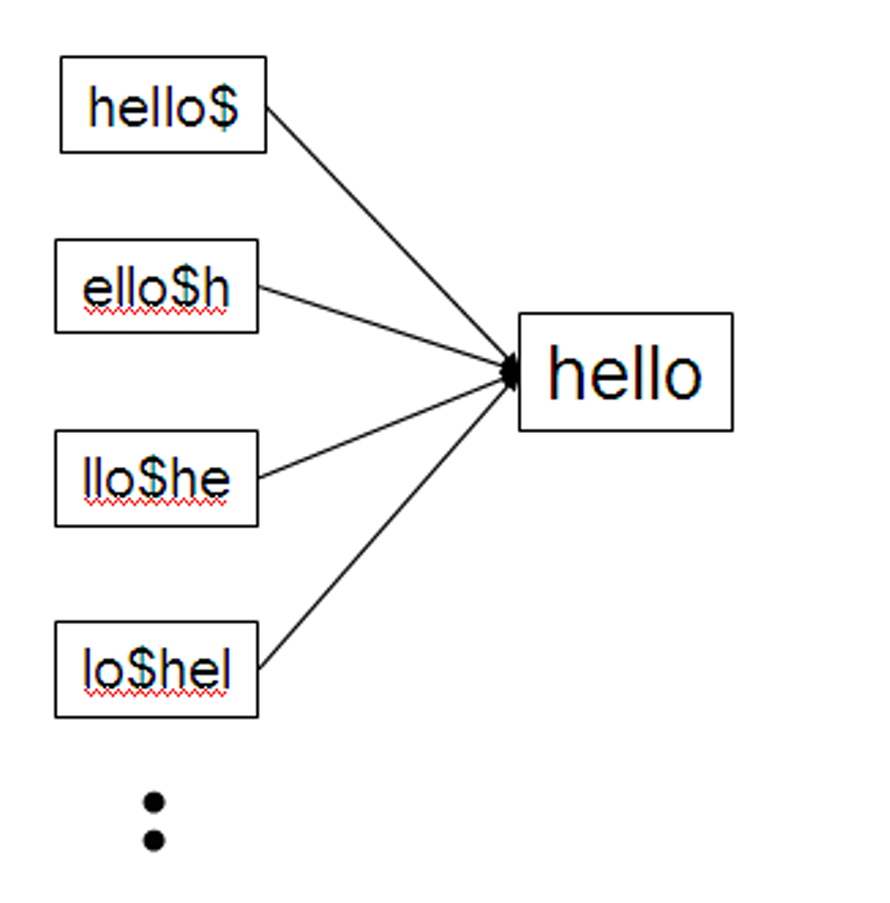
Permuterm index

왜 저렇게 저장하는 걸까?
아까 HELLO에 대해 hello,ello, elloh, llohe,lohe, lohel, o$hell, $hello 를 저장했다고 했다.
그러면 쿼리의 종류에 따라 아래처럼 처리할 수 있다.

- X: X$로 검색
- X*: $X*로 검색
- *X: X$*로 검색
- *X*: X*로 검색
- X*Y: Y$X* 로 검색

위 다섯 유형을 보자. 기본 검색인 X 빼고는 전부 *로 끝나게 해서 검색함을 알 수 있다!

예를 들어 hel*o를 검색하고 싶다면,

o$hel*

을 검색하면 된다. 그냥 간단하게 로테이션 돌려서 *가 단어 끝에 오게 해주면 끝이다.

퍼뮤텀 인덱스는 트리 구조로 구현되므로 permuterm tree라고 부르는 게 정확할 수 있지만, 일반적으로는 그냥 permuterm index라고 부른다.

Processing a lookup in the permuterm index

위처럼 와일드카드를 맨 오른쪽에 오게 로테이션 돌리고, B-tree 조회를 사용하면 된다.

근데 문제점은, Permuterm은 일반 B-tree에 비해 딕셔너리 크기가 4배 이상 크다. (경험적 수치)

k-gram indexes

공간을 효율적으로 쓰기 위해 k-gram index라는 것을 사용한다.
한 term에 발생하는 모든 문자 k-gram(k개의 문자 시퀀스)를 열거한다.

예시를 보자.

예시: "April is the cruelest month"
여기서 2-gram(=bigrams)을 얻을 수 있다.

$a ap pr ri il l$ $i is s$ $t th he e$ $c cr ru ue ul le es st t$ $m mo on nt th h$

저기서 $의 역할은 아까와 똑같이 special word boundary symbol이다.

bigrams에서 bigram을 포함하는 term으로 inverted index를 유지한다.

Postings list in a 3-gram inverted index

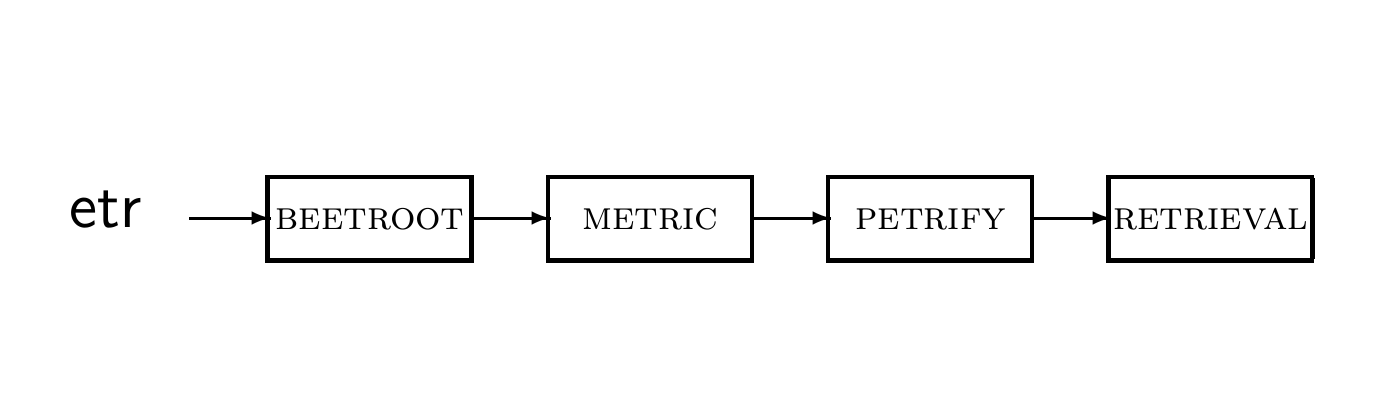
3-gram인 경우 사진처럼 inverted index 및 postings list를 유지할 수 있다.

k-gram (bigram, trigram, ...) indexes

우리는 이제 2가지 다른 유형의 inverted index를 다룰 수 있게 되었다.

  1. 용어로 구성된 쿼리를 기반으로 문서를 찾기 위한 term-document inverted index
  2. k-gram으로 구성된 쿼리를 기반으로 term을 찾기 위한 k-gram 인덱스

Processing wildcard terms in a bigram index

k-gram에 대해 위에서 배웠고, 그럼 wildcard를 어떻게 bigram index로 처리할 수 있을까?

예시: mon*
저 쿼리는 아래처럼 분해되어 실행된다.
$m AND mo AND on

mon으로 시작하는 모든 term을 찾겠다는 의미이다.

하지만 moon처럼 mon으로 시작하지 않는 false positives도 가져올 수 있다.

즉, 검색된 용어들 중 쿼리와 일치하지 않는 용어들을 걸러내야 한다. (후처리, postfiltering)

후처리를 통과한 용어들은 term-document inverted index에서 검색된다.

k-gram index와 permuterm index는 어떻게 다를까?

  • k-gram index는 공간 효율적이다.
  • Permuterm index는 후처리가 필요없다.

Exercise

또 구글을 예로 들어보겠다.

구글을 wildcard 쿼리에 대해 매우 제한적인 지원만을 하고 있다.

예를 들어, 구글에서 Geneva 대학교를 찾고 있는데, 프랑스어라 어떤 악센트를 사용해야 할지 몰라 아래처럼 검색하려고 했다고 하자.

gen* universit*

구글은 저걸 처리할 수가 없다.

관련해서 구글은 2010년 4월 29일에 아래와 같은 발표를 한 적이 있다.

Note that the * operator works only on whole words, not parts of words.

하지만 위는 사실이 아니다.
pythag*와 m*nchen을 검색해보면 알 수 있다.

왜 구글은 와일드카드 처리를 지원하지 못할까?

Processing wildcard queries in the term-document index

  • 문제 1: 많은 수의 부울 쿼리를 실행해야 한다.
    예를 들어 [gen* universit*]를 검색하려면 구글은
genevauniversity OR genevauniversit´e OR gen` eveuniversity OR gen`eveuniversit´e OR generaluniversities OR ...

저 무수한 길이의 쿼리를 죄다 실행해야 한다. 굉장히 비용이 크다.

  • 문제 2: 유저들은 입력하는 것을 싫어한다.
    만약 축약 쿼리가 허용된다면 유저들은 맨날맨날 저것만 쓰게 될 텐데, 앞서 말했듯이 비용이 크기 때문에 구글 입장에서는 굉장한 부담이 된다.

다만 위 문제는 Google Suggest로 다소 완화되었다고 한다.

4. Edit distance

Edit distance

  • 문자열 s1와 s2 사이의 edit distance는 문자열 s1을 s2로 변환하기 위해 필요한 최소한의 기본 작업 수를 의미한다.

edit distance를 계산하는 단계를 Levenshtein distance라고 부른다.
Levenshtein distance는 3단계로 나눌 수 있다. 1. 삽입 2. 삭제 3. 치환

예시1: dog-do: 1 (g 삽입)
예시2: cat-cart: 1 (t 삭제)
예시3: cat-cut: 1 (a->u 치환)
예시4: cat-act: 2 (c->a 치환, a->c 치환)

Damerau-Levenshtein distance는 Levenshtein distance에 4. 전위 라는 한 단계를 더 추가한다.
전위는 문자열 내 인접한 두 문자의 위치를 바꾸는 작업이다.
이 방법을 쓰면 cat-act이 c와 a의 위치를 바꾸는 1회의 작업으로 계산되어, 거리가 1이 된다.

Levenshtein distance: Computation

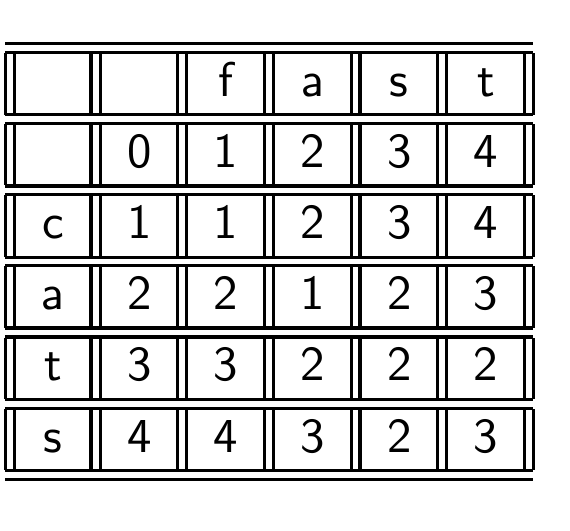
Levenshtein distance 표는 이렇게 그릴 수 있다.
a 빼고는 다 치환해야 해서 3이다. 어떻게 저 숫자가 나오는지는 아래에서 다루겠다.

Levenshtein distance: Algorithm

이 알고리즘은 두 문자열 사이의 편집 거리를 계산하기 위해 Dynamic Programming 방법을 사용한다. 즉, 문제를 작은 단위로 쪼개 해결한다는 것이다.

추가 설명 (by ChatGPT)
for i ← 0 to |s1|: 첫 번째 문자열 s1의 길이(즉, |s1|)까지 반복하는 루프를 시작합니다. 이는 행렬 m의 첫 번째 열을 초기화하는 데 사용됩니다.
do m[i, 0] = i: 행렬 m의 i번째 행, 첫 번째 열에 i값을 할당합니다. 이것은 문자열 s1에서 빈 문자열로 가는 데 필요한 삭제 작업의 수를 나타냅니다.
for j ← 0 to |s2|: 두 번째 문자열 s2의 길이(즉, |s2|)까지 반복하는 루프를 시작합니다. 이는 행렬 m의 첫 번째 행을 초기화하는 데 사용됩니다.
do m[0, j] = j: 행렬 m의 첫 번째 행, j번째 열에 j값을 할당합니다. 이것은 빈 문자열에서 문자열 s2로 가는 데 필요한 삽입 작업의 수를 나타냅니다.
for i ← 1 to |s1|: 문자열 s1의 각 문자에 대해 반복합니다. 이 반복은 실제로 두 문자열 간의 편집 거리를 계산하기 위한 동적 프로그래밍 테이블을 채우는 데 사용됩니다.
do for j ← 1 to |s2|: 문자열 s2의 각 문자에 대해 내부 반복을 시작합니다.
do if s1[i] = s2[j]: 이 조건문은 문자열 s1의 i번째 문자와 문자열 s2의 j번째 문자가 같은지 확인합니다.
then m[i,j] = min{m[i-1,j]+1, m[i,j-1]+1, m[i-1,j-1]}: 만약 문자가 같다면, 행렬 m의 현재 위치 m[i, j]를 계산하기 위해 삭제, 삽입, 치환 비용 중 최소값을 선택합니다. 여기서 m[i-1, j-1]은 치환 비용을 나타내며, 이 경우에는 문자가 같기 때문에 추가 비용 없이 이전 값이 그대로 사용됩니다.
else m[i,j] = min{m[i-1,j]+1, m[i,j-1]+1, m[i-1,j-1]+1}:
만약 문자가 다르다면, 행렬 m의 현재 위치 m[i, j]를 계산하기 위해 삭제, 삽입, 치환 작업 중 최소 비용을 더한 값에 1을 더해 최소값을 선택합니다.
return m[|s1|, |s2|]:
마지막으로, 행렬 m의 우측 하단 모서리, 즉 m[|s1|, |s2|] 값이 두 문자열 s1과 s2 사이의 Levenshtein 거리를 나타내며, 이 값을 반환합니다.

뭔 소리인가 싶을 거다.

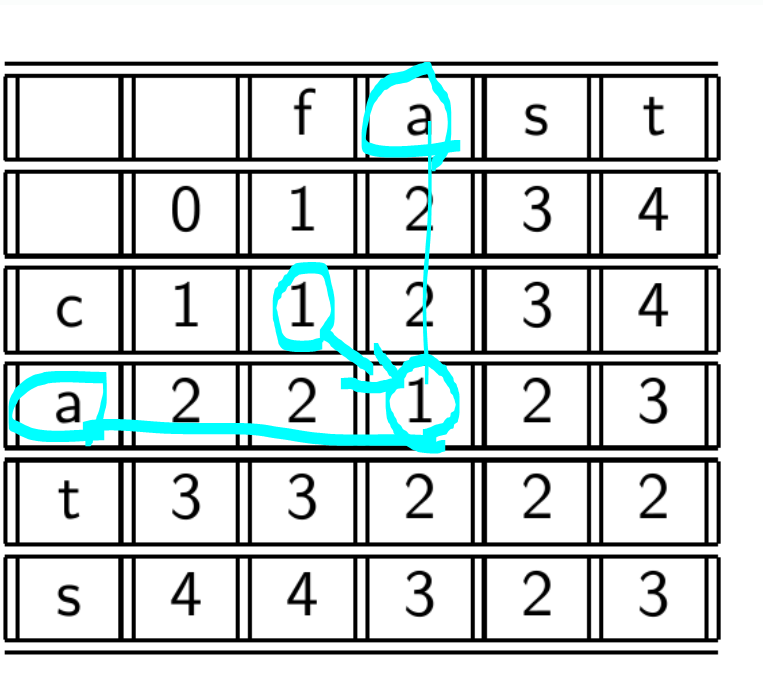
쉽게 말해 문자가 같으면 대각선 우측 하단으로는 더하지 않고 나머지 주변 3개는 다 1씩 더한다.

Levenshtein distance: Example

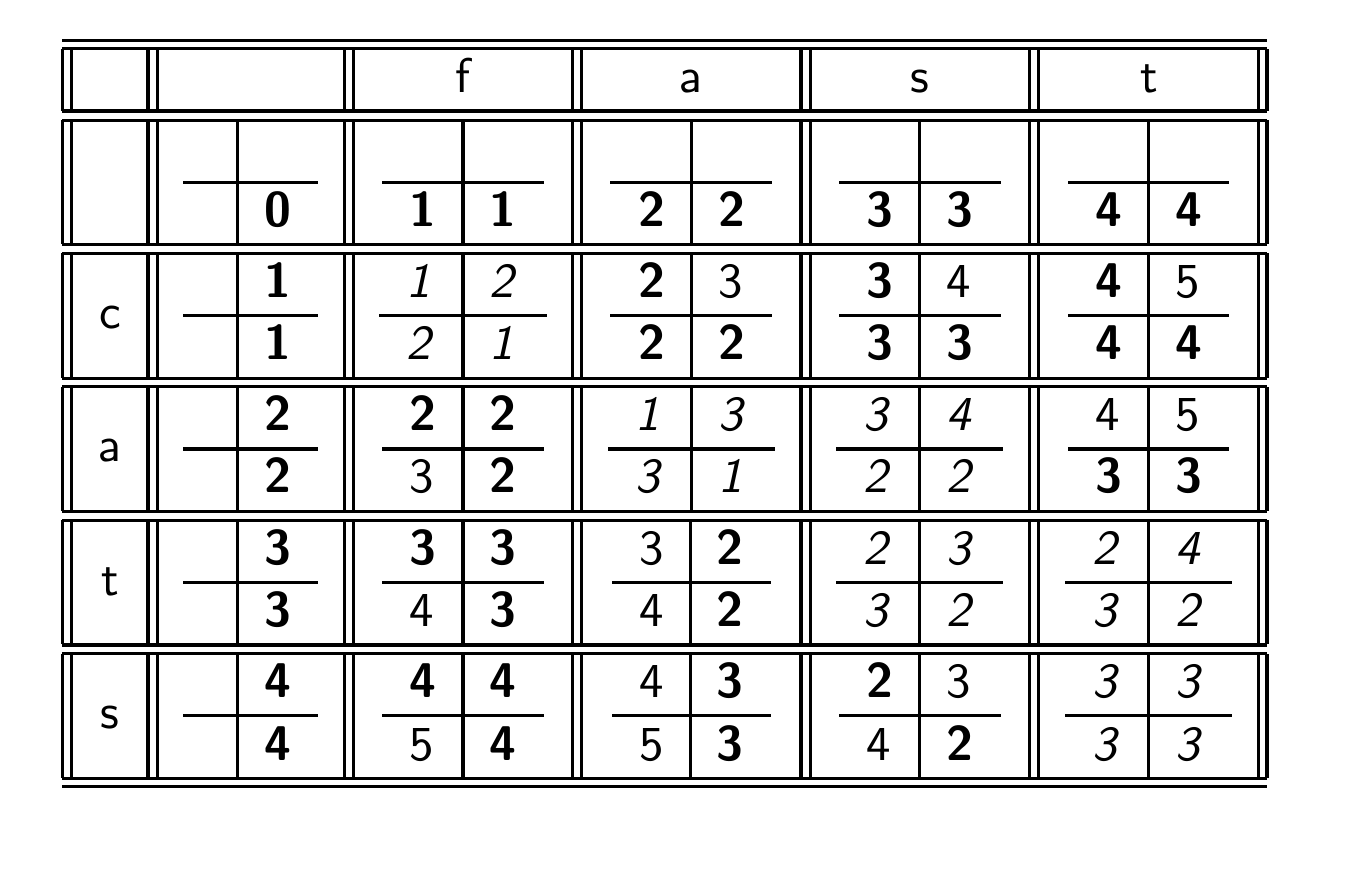
자세하게 그리면 이렇게 되는데, 상당히 복잡해서 이렇게까지 할 필요는 없다.

Each cell of Levenshtein matrix

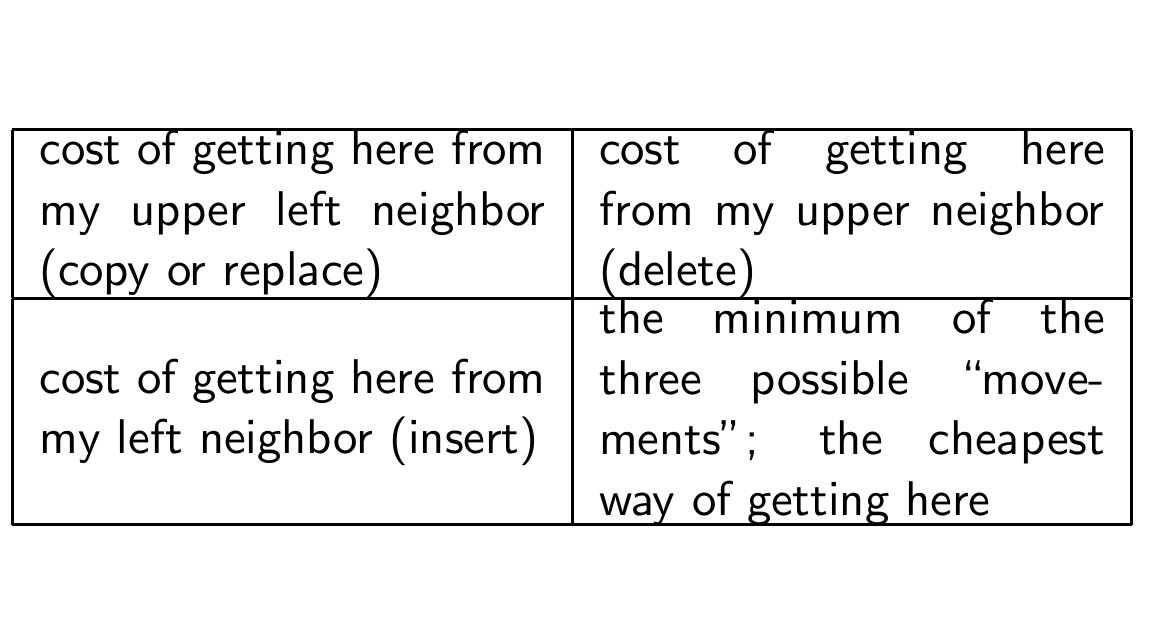
각 셀의 정보는 사진과 같다.

Dynamic programming (Cormen et al.)

동적 프로그래밍에는 두 가지 중요한 특성이 있다.

  1. Optimal Substructure (최적 부분 구조)
    문제의 최적 해결책은 하위 문제(subproblems)의 최적 해결책을 포함하고 있다. 즉, 큰 문제의 해결 방법이 작은 문제들의 해결 방법을 포함하고 있다.

  2. Overlapping Subsolutions (중복되는 하위 해결책들)
    하위 문제들의 해결책이 중복되어, brute-force 알고리즘을 전체 최적 해를 계산할 때 여러 번 계산된다.

이 특성들은 edit distance 문제에 활용된다.

  • edit distance에서의 하위 문제는 두 문자열의 prefixes에 대한 edit distance이다. 예를 들어, kitten과 sitting의 edit distance를 구할 때, kit-sit, ki-si 같은 게 하위 문제이다.
  • prefix의 거리를 오른쪽으로, 대각선 아래로, 아래로 3번 계산해야한다.

Weighted edit distance

edit distance와 유사하지만, 각 operation에 가중치가 부여된다.

  1. 가중치 부여: 작업의 비용이 작업에 관련된 문자에 따라 다 달라진다.
  2. 실수 감지: 키보드 입력 실수를 잡아내는데, m을 n으로 입력할 가능성이 m을 q로 입력할 가능성보다 더 높다.
    따라서 m을 n으로 바꾸는 작업의 weight edit distance가 m을 q로 바꾸는 작업보다 작아야 한다.
  3. 가중치 행렬 필요: 각 문자 쌍 사이의 치환 비용을 나타내는 가중치 행렬이 필요하다.
  4. 이러한 알고리즘을 다루기 위해 기존의 동적 프로그래밍 알고리즘을 수정하여 가중치를 다룰 수 있게 해야 한다.

Using edit distance for spelling correction

edit distance를 사용해서 철자를 교정할 수 있다.

먼저, 주어진 쿼리(잘못 입력된 단어나 문장)에 대해 설정된 edit distance 내에 있는 모든 가능한 문자 시퀀스를 열거한다. (weight 있을 수도 있음)

그 후, 생성된 word 시퀀스 집합과 정확한 단어들의 목록과의 교집합을 찾는다.

마지막으로 사용자에게 잘못된 입력을 올바른 철자로 교정하는 제안을 한다.

Exercise

직접 두 문제 모두 해보자.
알고리즘 이해 참고: https://hsp1116.tistory.com/41

  1. OSLO - SNOW의 Levenshtein distance matrix 계산
  1. cat을 catcat으로 변환하는 Levenshtein editing operation

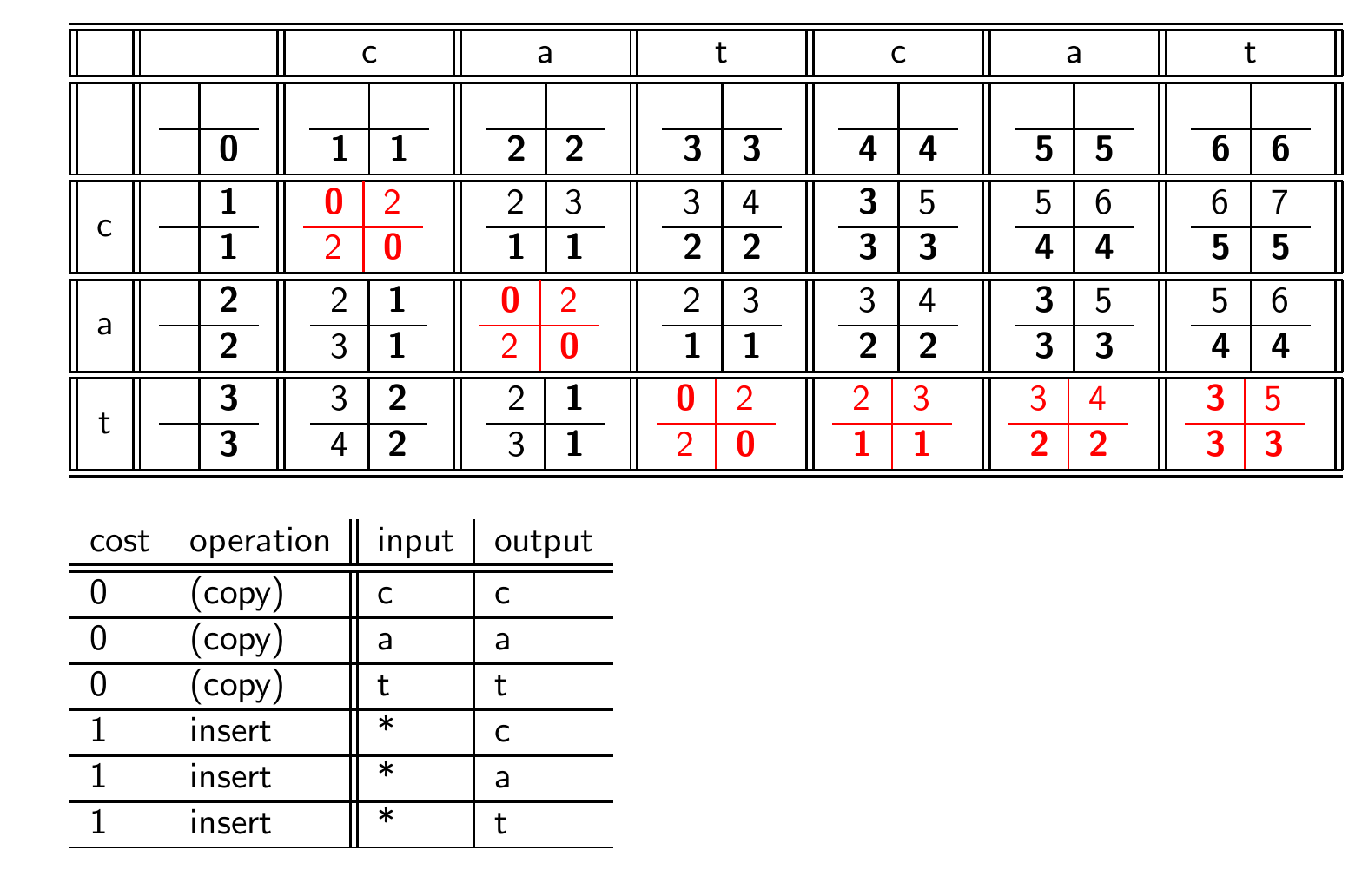
규칙

몇 번 연습해보며 규칙을 찾았다.
1. 빈 문자열에 대해 다 쓰기 0 1 2 3 4...
2. 두 문자가 같으면 대각선 아래로 바로 내림, 아니면 주변 3개 중에 제일 작은 거 골라서 1 더해서 씀

5. Spelling correction

Spelling correction

철자 교정의 두 가지 사용 사례

  • 문서 교정: indexing 과정에서 문서를 교정하는 데 사용됨.
  • 사용자 쿼리 교정: 사용자가 검색 엔진 등에서 입력한 쿼리의 오타를 교정함

두 가지 철자 교정 방법이 있다.
1. Isolated word spelling correction(독립된 단어 철자 교정)
각 단어를 개별적으로 확인하여 오타를 찾음.
an asteroid that fell form the sky
처럼 단어가 잘못된 문맥에서 사용되었을 때는 오타를 잡아내지 못한다. (form->from)

  1. Context-sensitive spelling correction(문맥을 고려한 철자 교정)
    주변 단어들을 보고 오타를 교정한다.
    form을 from으로 고칠 수 있다.

Correcting documents

사용자가 실시간으로 작성하는 문서의 오타를 잡아내는 것이 아니라, 주로 OCR 문서에 대해 교정한다.
예를 들어, 이미지 파일로부터 문자를 인식하여 텍스트 형식으로 변환하는 과정에서 생길 수 있는 잘못된 인식(e를 c로 인식하는 등)들을 수정하는 것이다.

이 때, 원본 문서는 변경하지 않는다는 IR의 철학을 치켜야 한다. 문서의 내용은 그대로 유지하면서, 검색 가능한 텍스트로 변환하는 과정에서 발생하는 오류들을 수정하는 데에 중점을 둔다.

Correcting queries

문서는 알겠고, 사용자 쿼리에서의 철자 교정은 어떻게 수행할까?

  • First: 독립된 단어 철자 교정=> 첫 번째 단계는 각각의 단어를 개별적으로 철자 교정하는 것이다.
  • 전제 조건1: 올바른 단어들의 목록이 있다고 가정할 때, 이 목록에서 올바른 철자를 얻는다.
  • 전제 조건2: 잘못된 단어와 올바른 단어 사이의 거리를 계산할 수 있는 방법이 있어야 한다.
  • 간단한 철자 교정 알고리즘: 잘못 철자된 단어와 가장 거리가 작은 올바른 단어를 반환한다.
  • 예시: informaton이라는 단어가 주어지면, 알고리즘은 information이라는 단어를 제안한다.
  • 올바른 단어의 목록: list of correct words, 우리가 가지고 있는 컬렉션 내의 모든 단어들의 어휘를 사용할 수 있다.

그런데 이게 왜 문제가 되는 걸까?
-> 문맥을 고려하지 못하기 때문

Alternatives to using the term vocabulary

철자 교정 시 term vocabulary를 선택할 때 사용할 수 있는 대안적인 자원

  • 표준 사전
  • 산업 특화 사전
  • 컬렉션의 term vocabulary 활용 (특정 컬렉션에서 사용되는 용어들의 어휘를 사용하며, 적절한 가중치를 적용함)

Distance between misspelled word and correct word

틀린 철자의 단어와 올바른 단어 사이의 거리를 재는 것에도 여러 방법이 있다.

  • Edit distance & Levenshtein distance
  • Weighted edit distance
  • k-gram overlap

Spelling correction

결과적으로 Spelling correction은 어떻게 할 수 있는 걸까?

  • edit distance: 위에서 배운 edit distance를 활용해 isolated word spelling correction을 수행할 수 있다. (아래 언급)
  • k-gram 인덱스
  • Context-sensitive
  • General issues

k-gram indexes for spelling correction

위에서 k-gram도 철자 교정에 활용할 수 있다고 했다.
구체적으로 어떻게 하는 것일까?

우선, k-gram index가 으레 그랬듯이 모든 k-gram을 열거한다.
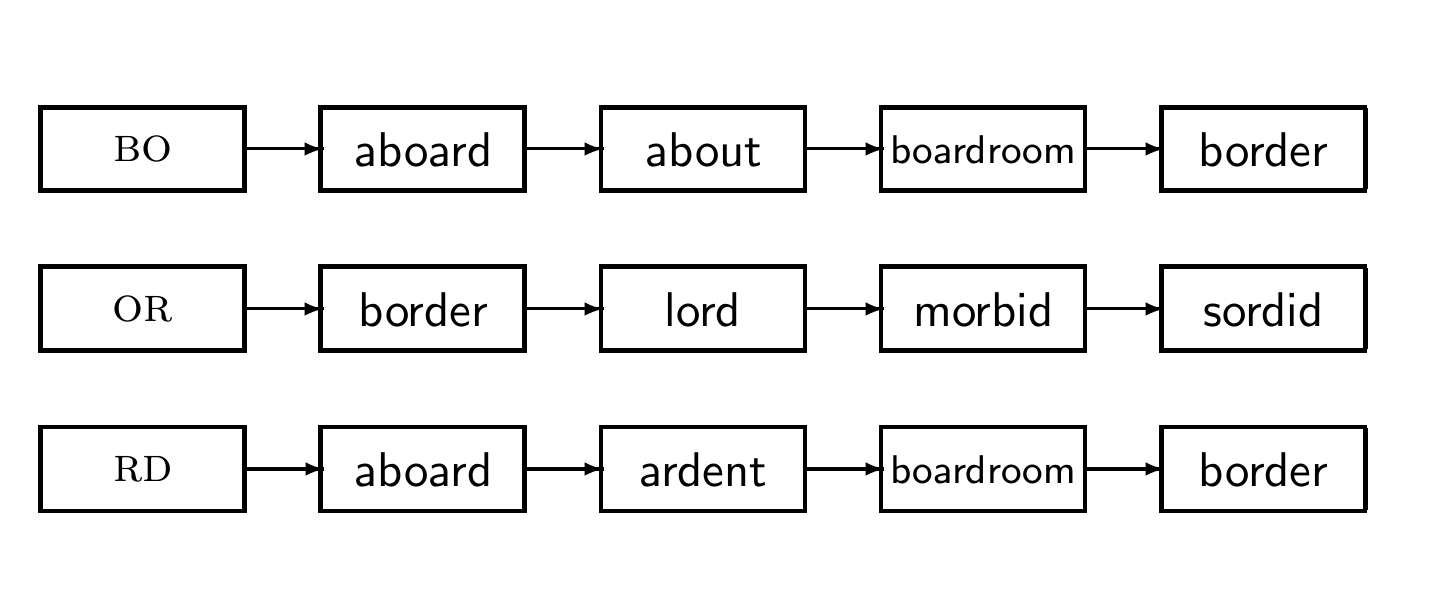
예시: bordroom을 bigram index로
-> bo or rd dr ro oo om

그 후, k-gram 인덱스를 사용하여 query term k-gram과 일치하는 올바른 단어를 검색한다.

교정할 단어와 올바른 단어 간의 유사도를 측정하기 위해 매칭되는 k-gram의 수를 기준으로 임계값을 설정한다.
예: 쿼리 용어와 최대 3개의 k-gram이 다른 단어만을 반환할 수 있도록 임계값을 설정할 수 있음

k-gram indexes for spelling correction: bordroom

Context-sensitive spelling correction

위에서는 한 단어에 대한 철자 교정만을 수행하였다.
문맥을 고려하려면 어떻게 해야 할까?

예시) an asteroid that fell form the sky

어떻게 form을 from으로 교정할 수 있을까?

-> hit-based spelling correction (히트 기반 철자 교정)
쿼리의 각 term에 가까운 올바른 용어들을 검색한다.
예를 들어 flew form munich => flea를 flew, from을 form, munch를 munich에 대한 교정어로 검색한다.

이후, 검색된 교정어로 가능한 모든 쿼리 문구를 생성하고, 각각을 쿼리로 시도한다.
한 번에 하나의 용어만 수정한다.

예시) flea form munich, flew from munich, flew form munch 등 많은 쿼리를 시도한다.

flew from munich가 가장 많은 히트(검색 결과)를 얻은 것으로 간주되어 올바른 쿼리로 선택된다.

그러면 만약, flew에 대해 8개의 대안, form에 대해 20개의 대안, munich에 대해 3개의 대안이 있으면 총 몇 개의 교정된 phrase를 열거할 수 있을까?
=> 8203=420가지

즉, 비효율적이다.

좀 더 효율적으로 하기 위해, 문서가 아닌 쿼리의 컬렉션을 살펴보는 방안이 있다.

General issues in spelling correction

철자 교정에서 고려해야 할 문제들이 있다.

  1. 유저 인터페이스
  • 자동 교정 vs 교정 제안
  • 여러 개의 가능한 교정이 있을 때 어떻게 표시할 것인가
  • simple vs powerful UI 간의 트레이드 오프
  1. 비용
  • 철자 교정은 계산적으로 비용이 많이 들 수 있는 작업이다.
  • 모든 쿼리를 실행하지 않으려면? > 매치되는 문서가 매우 적은 쿼리에 대해서만 철자 교정 수행
  • 그런데 주요 검색 엔진들의 철자 교정 기능은 매우 효율적이라서 모든 쿼리에 대해 실행될 수 있을 만큼 충분히 경제적이라고 한다. 물론 모든 검색 엔진이나 시스템이 이 수준의 효율성을 갖추고 있지는 않을 것이다.

Exercise: Understand Peter Norvig's spelling corrector

피터 노빅이 파이썬으로 작성한 간단한 철자 교정기이다.

참고 자료: https://americanopeople.tistory.com/347

이 알고리즘은 단어 레벨에서 동작하며, 문맥은 고려하지 않는다.

  1. 단어 사전을 가져온다.
  2. 분할, 삭제, 전치, 치환, 삽입 등 여러 유형 시뮬레이션
  3. 생성된 수정 후보들을 통해 올바른 단어를 찾음
  4. 가장 높은 빈도수를 가진 단어를 최종 수정안으로 선택

6. Soundex

Soundex

Soundex은 음성학적인 유사성에 기초하여, 단어의 철자가 다르더라도 비슷하게 발음되는 단어들을 매칭하는 데 사용된다.
phonetic을 찾기 위한 기초이다.

예를 들어, 'chebyshev'와 'tchebyscheff'는 철자는 다르지만 발음이 비슷하여 같은 Soundex 코드를 가질 수 있다.

Soundex algorithm

알고리즘은 다음과 같다.

  1. 각 token을 인덱싱하기 전 4자리로 줄인 형태로 변환한다.
  2. query terms에 대해서도 동일한 처리를 한다.
  3. 변환된 형태에 기반한 색인을 만들고 검색한다.

구체적으로는,

  1. 첫 글자 유지: 이는 Soundex 코드의 첫 번째 문자가 됨
  2. 다음 문자를 0으로 변경: A, E, I, O, U, H, W, Y (자기 주장이 약한 소리들이다)
  3. 나머지 철자를 다음과 같이 변경
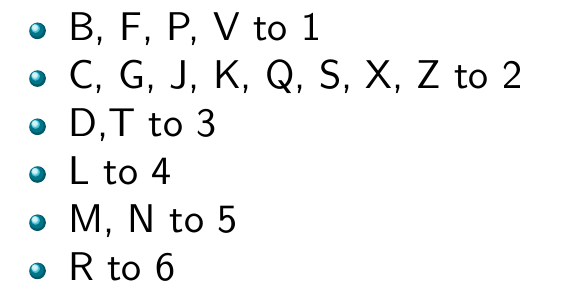
  4. 연속된 동일한 숫자 5쌍 중 하나씩을 반복해서 제거한다.
  5. 결과 문자열에서 모든 0을 제거하고, 제거한 코드의 길이가 4글자 미만인 경우 결과 문자열에 후행 0을 채워 반환

Example: Soundex of HERMAN

HERMAN이라는 단어를 예시로 들어보자.

H는 첫 글자이므로 유지한다.

E, A는 0으로 바꾼다.
-> 0RM0N

나머지 철자도 규칙대로 바꾼다.
-> 06505

0을 전부 삭제한다.
06565 -> 655

H655를 반환한다.

여기서 알 수 있는 점은, 만약 HERMANN이 입력됐다 하더라도 같은 코드를 반환했을 것이라는 거다.

0RM0NN
->065055
->06505 (연속된 숫자 중 하나 제거)
->655
->H655

How useful is Soundex?

이런 Soundex는 얼마나 정보검색에 적합한가?

사실 그닥 적합하지는 못하다.

그러나 다른 애플리케이션(예: 인터폴)의 high recall(고회상) 작업에는 좋다.

조벨과 다트는 IR에서 phonetic matching을 위한 더 나은 대안을 제시한 바 있다.

Exercise

내 성 가지고 Soundex code 계산해보기

EUN
=> E0N
=> E05
=> E0500

※ 추가로 공부할 점

  • Google Suggest가 제공하는 구글의 Wildcard 처리
  • Levenshtein distance 표 그리기
  • 파이썬으로 Levenshtein distance 그려보기
  • 피터 노빅 알고리즘 이해하기
  • Soundex 공부
  • 파이썬으로 Soundex 알고리즘 짜보기
  • 조벨과 다트가 제안한 게 뭔지 찾아보기
profile
hoho
이전 포스트

[Information Retrieval] 2. The term vocabulary and postings lists

다음 포스트

[Information Retrieval] 4. Index Construction

0개의 댓글