[CV Study] WEEK04- Swin Transformer: Hierarchical Vision Transformer using Shifted Windows

-·2022년 7월 13일

논문 설명을 잘 해주신 영상이 있어서, 이 영상을 주로 참고하여 정리해보았다. 목차 역시 영상의 순서를 따라가보려고 한다!

들어가기 전

2주차에 진행했던 ViT를 읽고, 그 후속연구에 대해서 공부하기로 했다. 참고로 ViT가 2020년 10월에 발표되었고, 그 이후 2021년 3월에 이 Swin Transformer 논문이 발표되었다. 지금까지도 Swin Transformer을 기반으로 논문이 아주 활발하게 발표되고 있다. 잠깐 찾아보니 medical image를 도메인으로 하는 swin-unet도 있고 그렇다.

1. Purpose

ViT의 한계

한정된 태스크 문제 : ViT 모델은 오직 분류 문제를 해결하기 위해 설계되었다.
이미지 도메인의 문제 : 다음은 도메인에 대한 문제가 있다. ViT는 텍스트 도메인에서 사용되었던 트랜스포머 구조를 그대로 가져와서 사용한다. 거의 수정을 하지 않는 것을 목표로 했기 때문에, 이미지 도메인을 위한 특성이 담겼다고 보기 어렵다.
연산량 : 연산량의 문제도 있다. ViT에서는 텍스트 토큰 대신 이미지 패치가 들어가게 되는데, 패치마다 self-attention을 수행하므로, 이미지의 패치(토큰)수가 증가할 수록 연산량이 quadratic하게 증가한다.

Purpose of Swin Transformer

Swin Transformer는 당연히, 위에서 언급한 ViT의 한계를 극복하기 위해 설계되었다.

분류 태스크에만 한정되지 않은, 다양한 목적의 backbone으로 사용될 수 있도록 하자!
Transformer 구조에 이미지 도메인만의 특성을 반영해보자!
더 적은 연산량으로 계산하자!

2. Notation

$M$ : Window size (patch 개수를 기준으로 count)
$n$ : Window 개수
$N$ : 이미지의 patch 개수

3. Background

ViT에 대한 사전 이해가 필요하다. 그러나 우리는 2주차에 보고 넘어갔으니 model overview만 남기고 생략..

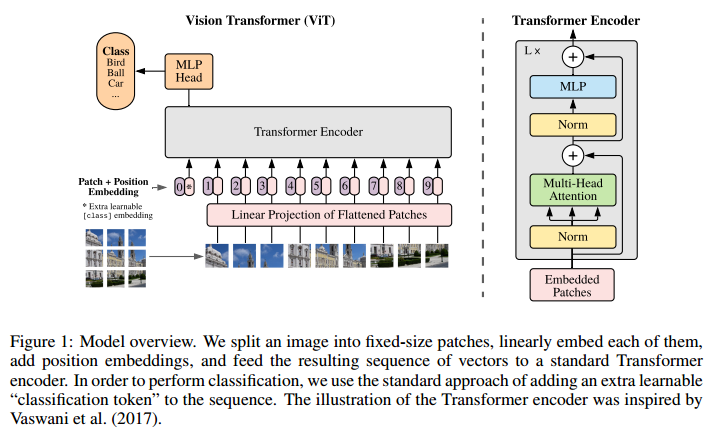
4. Solution

기존 ViT와는 다르게, 이미지 도메인의 특성을 고려한다. 그렇다면 이미지의 특성은 어떤 것이 있는지 보면, 두 가지로 정리할 수 있다.
- high resolution of pixels (높은 해상도)
- large variations in the scale of visual entities (물체의 다양한 크기)

1. Local Window

따라서 저자들은, 모델에 Local Window를 적용하는 방법을 제안한다.

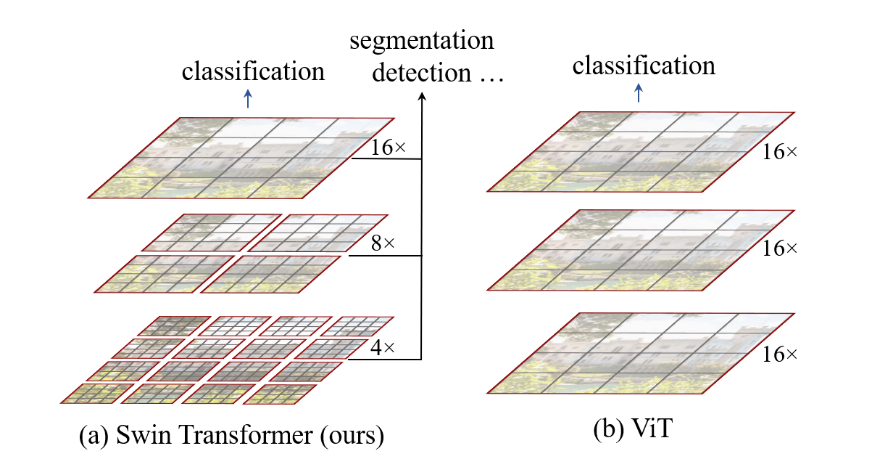
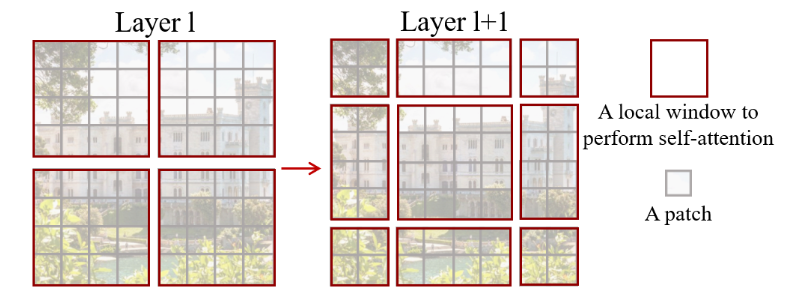
거두절미하고 figure를 보면, ViT와 Swin Trainsformer의 차이점과, Swin Trainsformer에 적용된 윈도우가 어떤 것인지 직관적으로 이해할 수 있다.
또한, Swin Trainsformer의 서로 다른 윈도우 크기를 갖는 Hierarchical 구조 역시 한 눈에 파악할 수 있다.
- {low-level에 각각 4개의 패치로 구성된 윈도우 내에서 각각 어텐션 진행 -> 다음 레이어로 넘어가서 패치를 합쳐서 새로운 윈도우 구성, 그 내에서 어텐션 진행 ...} 의 반복
  - 이것이 바로 Shifted WINdow!
- 즉, 각 계층마다 다른 해상도의 결과값을 얻을 수 있다. (각 레이어마다 보는 윈도우의 크기가 다르니까!)
- 이러한 특성으로 인해, segmentation이나 detection 등 다양한 태스크에도 적용 가능한 backbone 형태의 모델이라고 할 수 있다고 한다.
이 때, 두 모델 모두 classification을 하게 되는데, 차이점은 [cls] token을 사용하는 ViT와는 달리, Swin의 경우 [cls] token을 사용하지 않고, 그 대신 token들의 mean을 사용한다.

2. Low Complexity

Swin은 ViT보다 complexity도 적다.
ViT처럼 패치마다 self-attention을 하는 것이 아니라, 윈도우 내에서 self-attention을 수행하기 때문인듯?

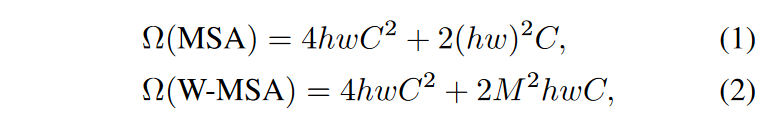
5. Method

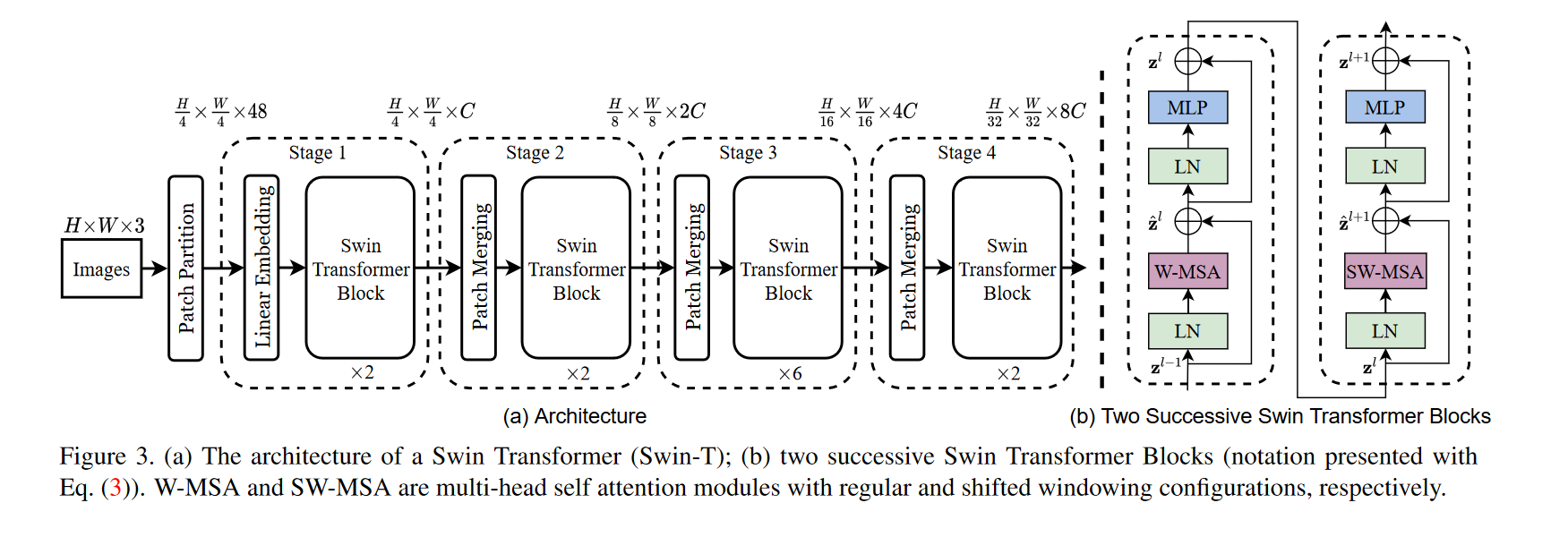
크게 두 가지의 구조, 네 가지의 스테이지로 구성되어있다.

Patch Merging

각각 다음 스테이지로 넘어가는 과정에서, Patch Merging이 이루어진다. 각 스테이지가 진행됨에 따라 해상도를 줄여주는 역할을 수행.
주변 이웃 패치의 정보를 가져와서, 하나의 차원으로 축소해주는 과정.
- 주변에 있는 2x2 사이즈로 이웃 패치 정보를 가져와서 하나의 차원으로 reduction하는 과정을 의미.
- 먼저, 하나의 패치가 C-dim이라면, 4C-dim으로 변환. 그 다음 linear production을 통해 2C-dim으로 reduction.

이러한 reduction을 "왜" 수행하는지에 대한 구체적인 설명은 논문에 없음.

참고한 동영상에 따르면, stage를 반복해나가면서 merging을 통해 reduction 없이 concat만 하게 되면, 차원이 엄청 커지기 때문에 이를 방지하기 위해 진행하지 않았나 추측함.
또, feature들의 결과를 서로 섞어주는 역할을 수행하게 된다.

Code :

 class PatchMerging(nn.Module):
  r""" Patch Merging Layer.
  Args:
      input_resolution (tuple[int]): Resolution of input feature.
      dim (int): Number of input channels.
      norm_layer (nn.Module, optional): Normalization layer.  Default: nn.LayerNorm
  """

  def __init__(self, input_resolution, dim, norm_layer=nn.LayerNorm):
      super().__init__()
      self.input_resolution = input_resolution
      self.dim = dim
      self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
      self.norm = norm_layer(4 * dim)

  def forward(self, x):
      """
      x: B, H*W, C
      """
      H, W = self.input_resolution
      B, L, C = x.shape
      assert L == H * W, "input feature has wrong size"
      assert H % 2 == 0 and W % 2 == 0, f"x size ({H}*{W}) are not even."
      
      # 입력 이미지는 높이 H와 폭 W의 크기를 갖도록 reshape
      x = x.view(B, H, W, C) 
			
      # 입력의 벡터화, 네 부분으로 나누게 된다. H/2 W/2이므로, 각 벡터는 입력의 1/4.
      x0 = x[:, 0::2, 0::2, :]  # B H/2 W/2 C
      x1 = x[:, 1::2, 0::2, :]  # B H/2 W/2 C
      x2 = x[:, 0::2, 1::2, :]  # B H/2 W/2 C
      x3 = x[:, 1::2, 1::2, :]  # B H/2 W/2 C
      
      # 4개의 벡터 concat, 4개의 벡터이므로 채널은 4*C
      x = torch.cat([x0, x1, x2, x3], -1)  # B H/2 W/2 4*C
      x = x.view(B, -1, 4 * C)  # B H/2*W/2 4*C
      
      #  linear production을 통해 4C-dim -> 2C-dim으로 reduction
      x = self.norm(x)
      x = self.reduction(x)

      return x

  def extra_repr(self) -> str:
      return f"input_resolution={self.input_resolution}, dim={self.dim}"

  def flops(self):
      H, W = self.input_resolution
      flops = H * W * self.dim
      flops += (H // 2) * (W // 2) * 4 * self.dim * 2 * self.dim
      return flops

Swin Transformer Block

(b)에서 자세한 figure를 볼 수 있다. 왼쪽과 오른쪽은 연속적으로 이어진 구성이고, (a)의 각 스테이지 아래의 X는, (b)의 페어가 적용된 횟수를 의미함.
첫 번째 Swin Transformer Block에서의 MSA은, W-MSA(Window Multi-head Self Attention)라고 하며, 두 번째에서는 SW-MSA(Shifted Window Multi-head Self Attention)라고 함.
또 Efficient batch Computation, Relative Position Bias, Cyclic Shift and Attention Mask 등의 detail도 있는데 아래에서 추가로 설명할 예정.

W-MSA(Window Multi-head Self Attention)

Local Window 내부에서의 Self attention
이미지에 포함된 윈도우 내에서 각각, 독립적으로 별도로 self-attention을 진행하는 방법.
self-attention의 횟수는 local 윈도우의 개수.

이 때, 이미지 하나에 대해서만 attention을 적용하는 것이 아닌 윈도우 단위로 attention을 $n$ 번 적용해야 하기 때문에, 연산이 더 많아지게 된다. 이런 연산량을 해결하기 위하여 등장한 것이 Efficient batch Computation이다.

(1) Efficient batch Computation

$n$ 개의 윈도우를 배치와 같은 차원으로 합쳐서, 한 번에 병렬적으로 연산하는 방법이다.
반복해서 연산을 하는 것이 아닌, 병렬 처리를 통해 빠르게 계산!

(2) Relative Position Bias는

두 축마다, Relative Position의 범위가 $[-M+1, M-1]$ 로 이루어짐
Bias Matrix $\hat{(B)}$ 은 $\mathbb{R}^{(2M-1)*(2M-1)}$ 차원으로 구성이 되어있음.
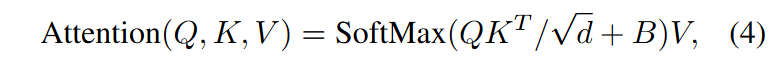
이 수식에서 $B$ 는 $\hat{(B)}$ 에서 값을 가져와서 사용하게 됨.
그렇다! ViT에서 NLP처럼 넣어주던 position embedding은 절대 좌표를 앞에 더해주는 식이었는데, 저자들은 그러한 pos embed보다 이 상대적인 position을 더해주는 것이 더 좋다고 이야기한다.

더 자세히..

그래서 이게 무슨 의미인가? 영상에서 소개한 예시를 통해 이해해보자.
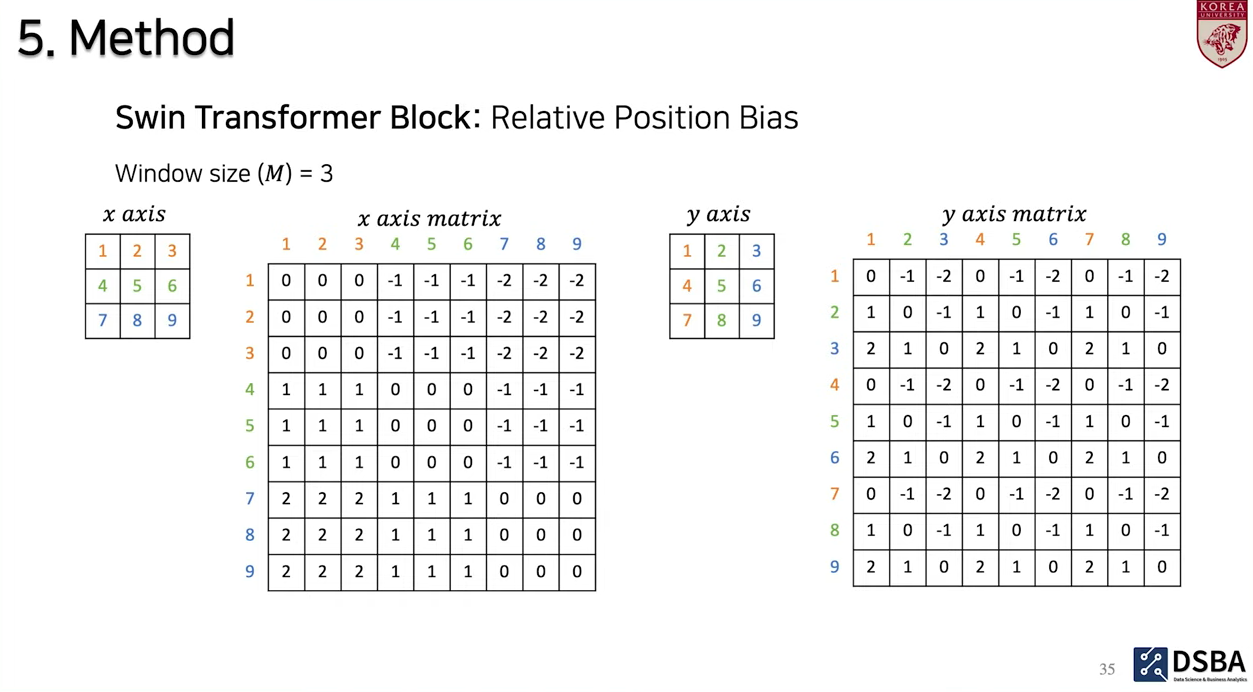
예시에서 윈도우 사이즈 $n$ 은 3. x축과 y축을 기준으로 서로 다른 기준을 두어 Relative position을 나타낼 수 있다고 함.
먼저, x축 기준으로 생각해보면 각 x축에 대해 서로 다른 색으로 표시가 됨. 먼저 1에 대해서 보면, 자기 자신과의 거리는 0. 1과 2에 대해서도 같은 축에 있기 때문에 거리가 0. 그런데 1과 4를 보게 되면 다음 축에 존재하기 때문에 거리가 -1, 1과 7은 거리가 -2.
y축을 기준으로 보면, 자기 자신과는 0. 그러나 1과 2를 보게 되면 다른 축에 있기 때문에 거리가 -1... 이런 식으로 거리마다 값(bias)를 확인할 수 있음.
이렇게 구성된 각각의 axis matrix에 대해, 각각 { $M -1$ }을 더해주게 됨. 이는 즉, 음수가 포함된 범위를 인덱스로 사용하기 위해 0부터 시작되게 하기 위함.
그 다음은, x축의 모든 element에 대해, { $2M-1$ } 값을 곱해주게 됨.
그 다음 axis matrix들을 더해주게 되면, 최종적으로 relative position index matrix를 얻게 됩니다.
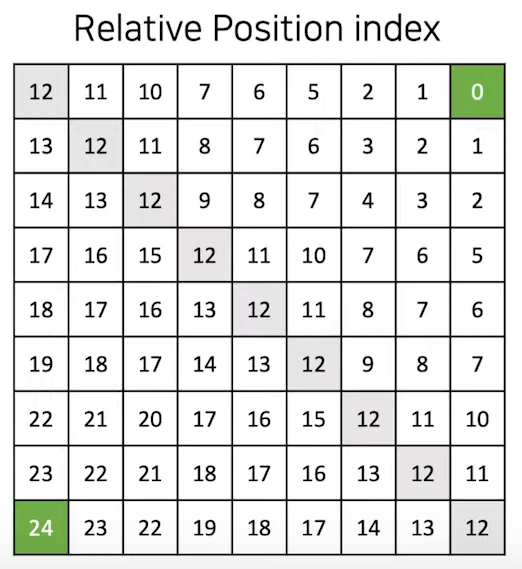
max value가 24인 이유는, $\hat{(B)}$ 의 차원이 $\mathbb{R}^{(2M-1)*(2M-1)}$ 였는데, $2M-1 = 2*3-1 = 5$ 이기 때문에 $5*5 = 25$ 이기 때문이다.
그 다음 $\hat{(B)}$ 으로 부터 $B$ 값을 얻고, 이를 Q@K를 스케일링 한 값에 더하여 소프트맥스 통과하고, V를 곱해주는 것이 수식4에 대한 설명이다.
결론적으로, 이 논문에서는 Relative Position Bias를 사용하여서, 보다 적은 파라미터로, 넓은 범위의 Relative Position을 학습할 수 있다고 이야기한다.

어쨋든 Code:

class WindowAttention(nn.Module):
  r""" Window based multi-head self attention (W-MSA) module with relative position bias.
  It supports both of shifted and non-shifted window.
  Args:
      dim (int): Number of input channels.
      window_size (tuple[int]): The height and width of the window.
      num_heads (int): Number of attention heads.
      qkv_bias (bool, optional):  If True, add a learnable bias to query, key, value. Default: True
      qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
      attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
      proj_drop (float, optional): Dropout ratio of output. Default: 0.0
  """

  def __init__(self, dim, window_size, num_heads, qkv_bias=True, qk_scale=None, attn_drop=0., proj_drop=0.):

      super().__init__()
      self.dim = dim
      self.window_size = window_size  # Wh, Ww
      self.num_heads = num_heads
      head_dim = dim // num_heads
      self.scale = qk_scale or head_dim ** -0.5

      # define a parameter table of relative position bias
      self.relative_position_bias_table = nn.Parameter(
          torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads))  # 2*Wh-1 * 2*Ww-1, nH

      # get pair-wise relative position index for each token inside the window
      coords_h = torch.arange(self.window_size[0])
      coords_w = torch.arange(self.window_size[1])
      coords = torch.stack(torch.meshgrid([coords_h, coords_w]))  # 2, Wh, Ww
      coords_flatten = torch.flatten(coords, 1)  # 2, Wh*Ww
      relative_coords = coords_flatten[:,
      :, None] - coords_flatten[:, None, :]  # 2, Wh*Ww, Wh*Ww
      relative_coords = relative_coords.permute(1, 2, 0).contiguous()  # Wh*Ww, Wh*Ww, 2
      relative_coords[:, :, 0] += self.window_size[0] - 1  # shift to start from 0
      relative_coords[:, :, 1] += self.window_size[1] - 1
      relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
      relative_position_index = relative_coords.sum(-1)  # Wh*Ww, Wh*Ww
      self.register_buffer("relative_position_index", relative_position_index)

      self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
      self.attn_drop = nn.Dropout(attn_drop)
      self.proj = nn.Linear(dim, dim)
      self.proj_drop = nn.Dropout(proj_drop)

      trunc_normal_(self.relative_position_bias_table, std=.02)
      self.softmax = nn.Softmax(dim=-1)

  def forward(self, x, mask=None):
      """
      Args:
          x: input features with shape of (num_windows*B, N, C)
          mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
      """
      B_, N, C = x.shape
      qkv = self.qkv(x).reshape(B_, N, 3, self.num_heads, C // self.num_heads).permute(2, 0, 3, 1, 4)
      q, k, v = qkv[0], qkv[1], qkv[2]  # make torchscript happy (cannot use tensor as tuple)

      q = q * self.scale
      attn = (q @ k.transpose(-2, -1))

      relative_position_bias = self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
          self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1)  # Wh*Ww,Wh*Ww,nH
      relative_position_bias = relative_position_bias.permute(2, 0, 1).contiguous()  # nH, Wh*Ww, Wh*Ww
      attn = attn + relative_position_bias.unsqueeze(0)

      if mask is not None:
          nW = mask.shape[0]
          attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
          attn = attn.view(-1, self.num_heads, N, N)
          attn = self.softmax(attn)
      else:
          attn = self.softmax(attn)

      attn = self.attn_drop(attn)

      x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
      x = self.proj(x)
      x = self.proj_drop(x)
      return x

  def extra_repr(self) -> str:
      return f'dim={self.dim}, window_size={self.window_size}, num_heads={self.num_heads}'

  def flops(self, N):
      # calculate flops for 1 window with token length of N
      flops = 0
      # qkv = self.qkv(x)
      flops += N * self.dim * 3 * self.dim
      # attn = (q @ k.transpose(-2, -1))
      flops += self.num_heads * N * (self.dim // self.num_heads) * N
      #  x = (attn @ v)
      flops += self.num_heads * N * N * (self.dim // self.num_heads)
      # x = self.proj(x)
      flops += N * self.dim * self.dim
      return flops

SW-MSA(Shifted Window Multi-head Self Attention)
- Goal : W-MSA 적용 이후, Local Window 간의 Self attention을 적용하자.
- 연결되어있지 않았던 부분에 대하여 윈도우가 적용되었음을 확인할 수 있음.
- layer l+1 그림을 보면, window의 개수가 처음에 비하여 가로 세로 하나씩 더 증가한 것을 확인할 수 있다. 2*2개에서 3*3개로 늘어났다!
- 따라서, 윈도우의 개수가 증가하여 연산이 비효율적으로 이루어지게 된다.
- 이를 해결하기 위하여 제안한 방식이 Cyclic Shift and Attention Mask, 이를 통해 W-MSA와 동일한 윈도우 개수를 사용하게 된다.
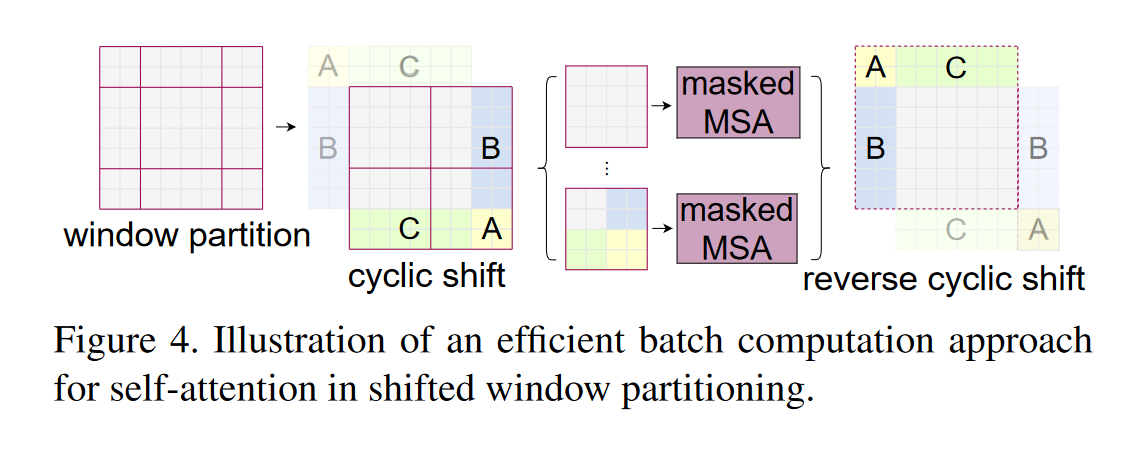
- cyclic shift : window_size//2만큼 우측 하단으로 shift하고, ABC 구역에 mask를 씌워서 self-attention이 이루어지지 않도록 한다. (반대쪽 경계에 있는 애들과는 att. 계산 하지 않기 위해서!)
- 같은 색의 블록은 cyclic shift되고, mask를 적용하여 각각 self-attention이 진행되는데, 4개의 윈도우를 사용하여, local 윈도우 간 attnetion을 계산하게 된다.
- 최종적으로 마지막 결과를 reverse로 적용하여, 원래 이미지로 복원한다.
- 여기서의 attention mask는 수식 4의 bias를 더해준 값에 더해지게 된다. 따라서 m2*m2의 차원을 가져야 한다.
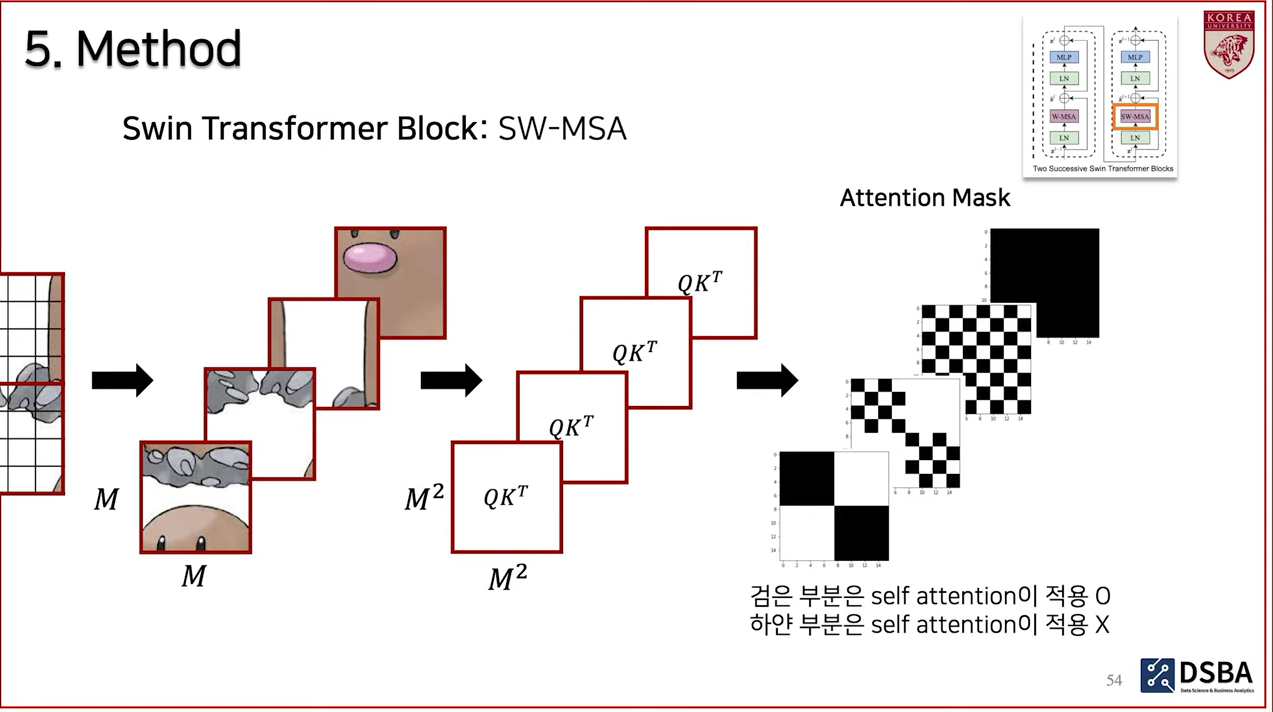
- 영상에서는 att. amsk를 찍어보았을 때 다음과 같이 나타나는 것을 확인할 수 있었다고 한다.
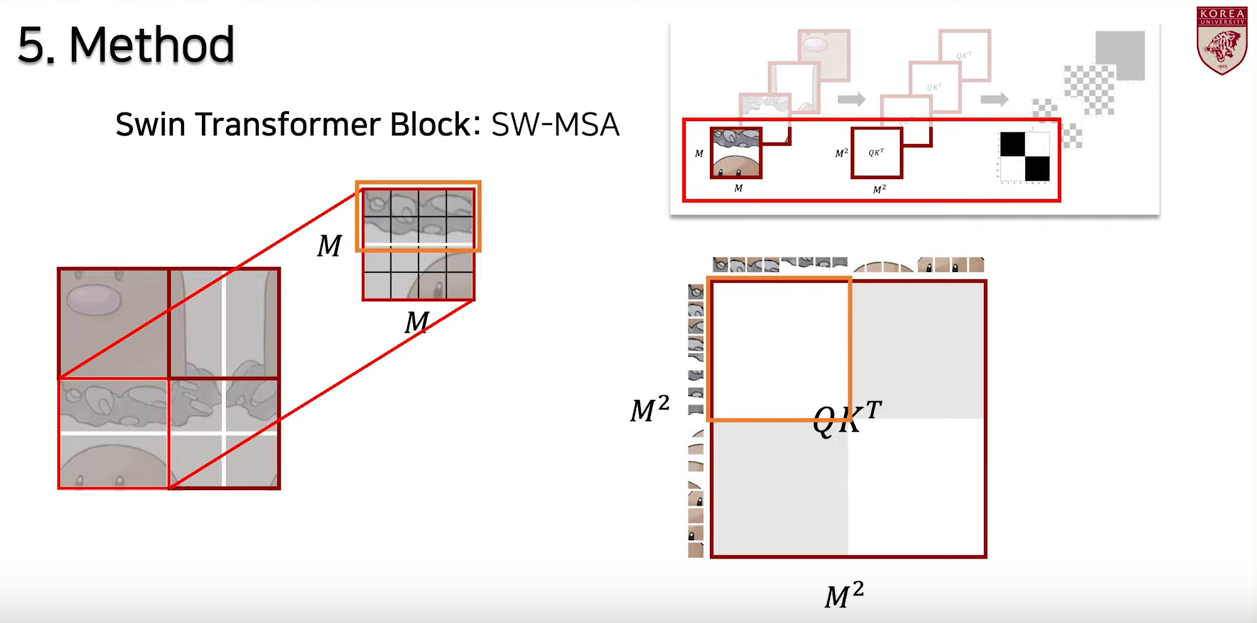
- 이런 식으로 self-attention이 이루어지고 있다!...

class SwinTransformer(nn.Module):
    def __init__(self, img_size=224, patch_size=4, in_chans=3, num_classes=1000,
                 embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24],
                 window_size=7, mlp_ratio=4., qkv_bias=True, qk_scale=None,
                 drop_rate=0., attn_drop_rate=0., drop_path_rate=0.1,
                 norm_layer=nn.LayerNorm, ape=False, patch_norm=True,
                 use_checkpoint=False, fused_window_process=False, **kwargs):
        super().__init__()

        self.num_classes = num_classes
        self.num_layers = len(depths)
        self.embed_dim = embed_dim
        self.ape = ape
        self.patch_norm = patch_norm
        self.num_features = int(embed_dim * 2 ** (self.num_layers - 1))
        self.mlp_ratio = mlp_ratio

        # split image into non-overlapping patches
        self.patch_embed = PatchEmbed(
            img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim,
            norm_layer=norm_layer if self.patch_norm else None)
        num_patches = self.patch_embed.num_patches
        patches_resolution = self.patch_embed.patches_resolution
        self.patches_resolution = patches_resolution

        self.pos_drop = nn.Dropout(p=drop_rate)

        # stochastic depth
        dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))]  # stochastic depth decay rule

        # build layers
        self.layers = nn.ModuleList()
        for i_layer in range(self.num_layers):
        	# BasicLayer = A basic Swin Transformer layer for one stage.
            layer = BasicLayer(dim=int(embed_dim * 2 ** i_layer),
                               input_resolution=(patches_resolution[0] // (2 ** i_layer),
                                                 patches_resolution[1] // (2 ** i_layer)),
                               depth=depths[i_layer],
                               num_heads=num_heads[i_layer],
                               window_size=window_size,
                               mlp_ratio=self.mlp_ratio,
                               qkv_bias=qkv_bias, qk_scale=qk_scale,
                               drop=drop_rate, attn_drop=attn_drop_rate,
                               drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
                               norm_layer=norm_layer,
                               downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
                               use_checkpoint=use_checkpoint,
                               fused_window_process=fused_window_process)
            self.layers.append(layer)

        self.norm = norm_layer(self.num_features)
        self.avgpool = nn.AdaptiveAvgPool1d(1)
        self.head = nn.Linear(self.num_features, num_classes) if num_classes > 0 else nn.Identity()

        self.apply(self._init_weights)

    def _init_weights(self, m):
        if isinstance(m, nn.Linear):
            trunc_normal_(m.weight, std=.02)
            if isinstance(m, nn.Linear) and m.bias is not None:
                nn.init.constant_(m.bias, 0)
        elif isinstance(m, nn.LayerNorm):
            nn.init.constant_(m.bias, 0)
            nn.init.constant_(m.weight, 1.0)

    @torch.jit.ignore
    def no_weight_decay(self):
        return {'absolute_pos_embed'}

    @torch.jit.ignore
    def no_weight_decay_keywords(self):
        return {'relative_position_bias_table'}

    def forward_features(self, x):
        x = self.patch_embed(x)
        x = self.pos_drop(x)

        for layer in self.layers:
            x = layer(x)

        x = self.norm(x)  # B L C
        x = self.avgpool(x.transpose(1, 2))  # B C 1
        x = torch.flatten(x, 1)
        return x

    def forward(self, x):
        x = self.forward_features(x)
        x = self.head(x)
        return x

    def flops(self):
        flops = 0
        flops += self.patch_embed.flops()
        for i, layer in enumerate(self.layers):
            flops += layer.flops()
        flops += self.num_features * self.patches_resolution[0] * self.patches_resolution[1] // (2 ** self.num_layers)
        flops += self.num_features * self.num_classes
        return flops

7. Experiments

Method 끝 ! 실험으로 가자 케케

Architecture Variants.

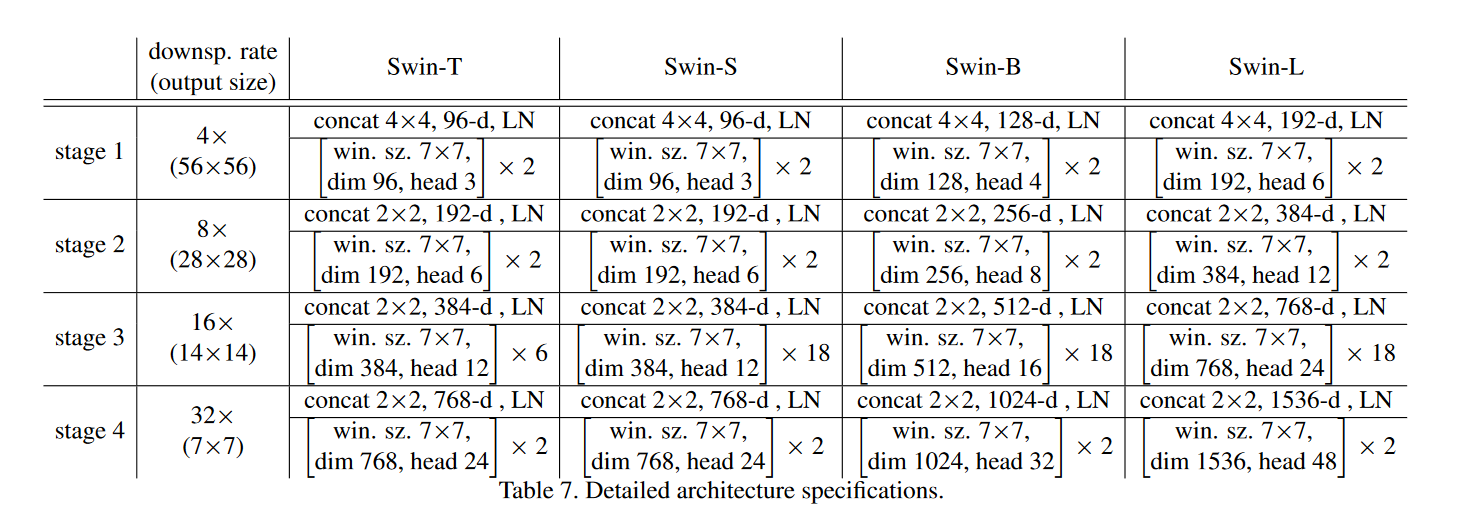
supplement의 테이블을 가져왔다. 기본적으로 input은 [224*224*3] 를 사용하였고 윈도우 사이즈는 7이다. 뒤 실험에서 input이 [384*384*3]인 경우도 있는데, 이 때는 윈도우 사이즈를 12를 사용했다고 한다.

Experiments settings.

Image Classification에 ImageNet-1K, Object Detection에 COCO 2017, 마지막으로 Semantic Segmentation에 ADE20K을 사용. 모두 동일하게 pre-trained에는 ImageNet-22K를 사용했음.
추가로, 저자들은 다양한 augmentation과 regulazation이 필요하다고 함. ViT에서도 이야기했지만, inductive bias가 적기 때문에...!
ViT에서 중요했던 repeated aug.와 EMA는 더 이상 성능에 큰 영향을 주지 못함.
optimizer로는 다른 최근 연구에서 사용하는 AdamW를 채택.

그 외에도..

Relative Positional Bias 여부,
Shifted Window 여부,
Window 적용 방법에 따른 속도 비교,
Sliding Window와 Shifted Window에 따른 실험 등을 진행했다.

Baseline으로는 CNN계열과 ViT 계열(ViT, DeiT) 모두를 사용하였다.
- DeiT는 ViT보다 더 적은 데이터로, Knowledge distillation과 regulazation을 통해 성능을 향상시킨 모델.

Classification

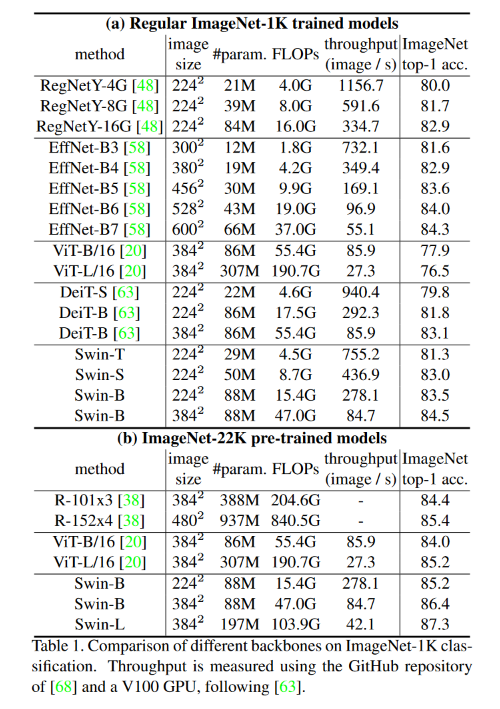
ImageNet-1K
- 성능은 비슷하나, 성능과 학습 속도의 trade-off가 더 작음.
ImageNet-22K
- 더 적은 파라미터로 좋은 성능.

왜 그럴까? 발표자의 생각으로는, ViT는 Local Window 개념이 없어서 Inductive bias가 더 적다. 따라서 사전학습 데이터의 양이 중요함.

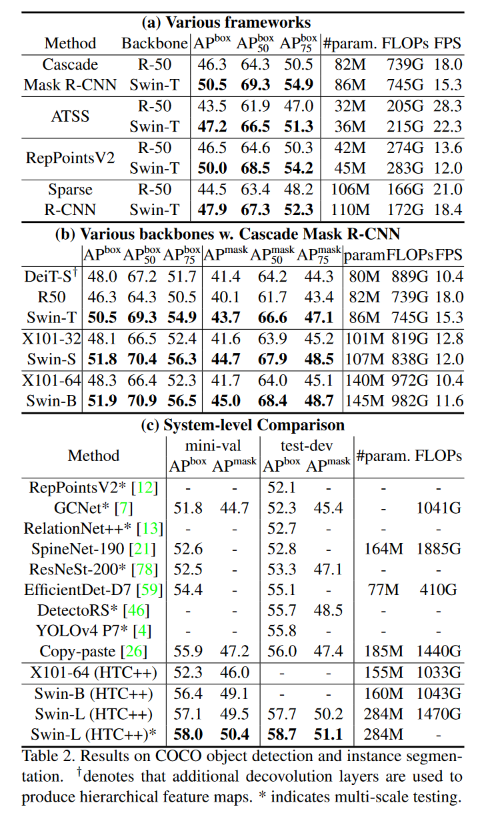
Object Detection

Frameworks 기준
backbone 기준

Semantic Segmentation

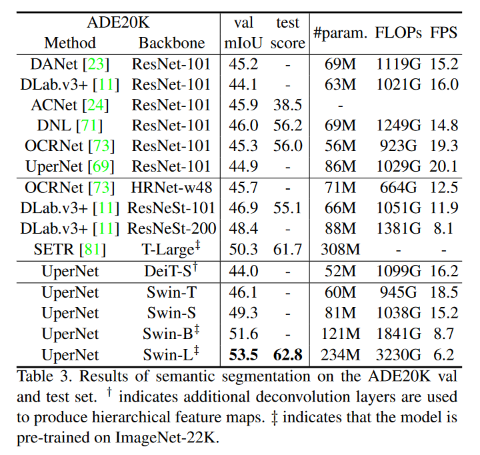
적은 파라미터로 좋은 성능.

Ablation Study

Shifted Window

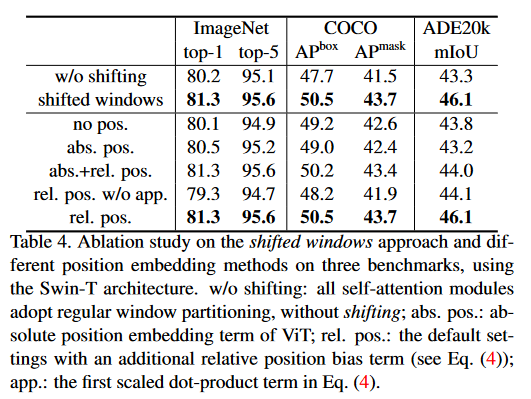
윈도우 간 관계를 학습하는 것이 Detection과 Segmentation 성능 향상에 도움이 된다.

Relative Positional Bias

semantic seg.에 큰 도움이 된다.
dense prediction에 직접적인 기여를 하기 때문...!

Window 적용 방법에 따른 속도 비교

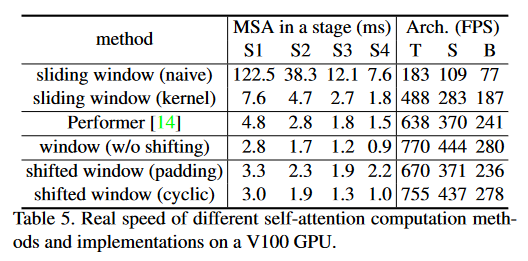
첫 행과 마지막 행 비교해보면 속도 차이가 엄청나다 ..

Sliding Window와 Shifted Window

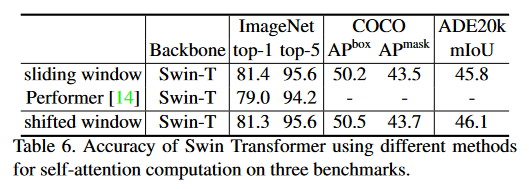
더 빠른 속도로 동일한 성능.

7. Conclusion

모델 구조

local window를 적용하여, inductive bias를 주입
patch merging을 통해, 계층 구조 형성

Contribution

이미지 특성 고려
다양한 vision task
더 적은 computation complexity

Code

MS에서 제공하는 official code가 있다.

후기

어떤 연구를 진행해볼수 있을까?

Reference 🔥

https://youtu.be/2lZvuU_IIMA
https://github.com/microsoft/Swin-Transformer
https://greeksharifa.github.io/computer%20vision/2021/12/14/Swin-Transformer/

이전 포스트

[Story Generation] Paper Review : A Corpus and Cloze Evaluation for Deeper Understanding of Commonsense Stories

다음 포스트