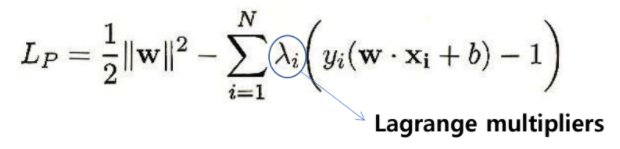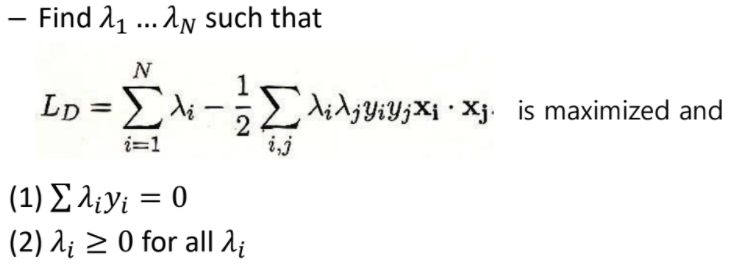Linear Separators
- Data를 분리할 linear hyperplane 찾기 (decision boundary, 결정 경계)
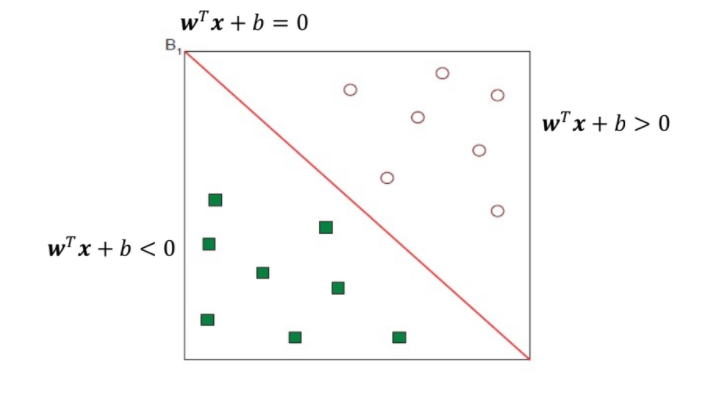
wT : θ , b:w0
Another Possible Solution
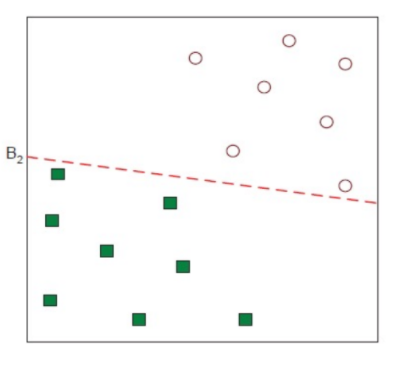
💡 그렇다면 어떤 linear separator가 가장 적합할까? (optimal)
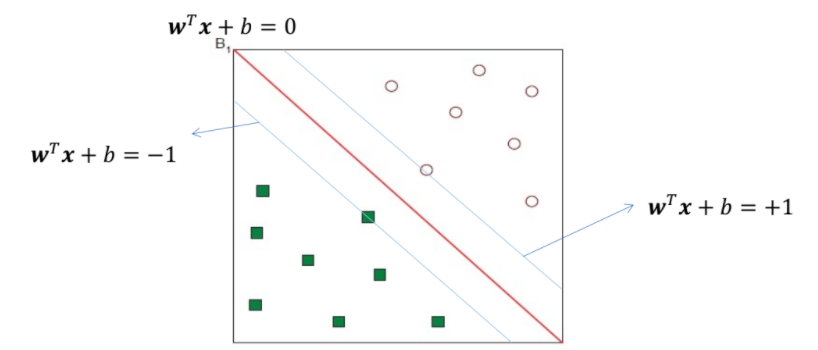
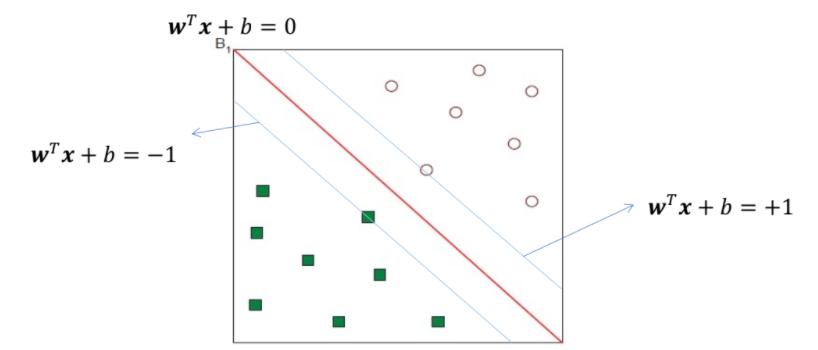
💡 B1, B2 중에 어떤 게 더 좋을까?
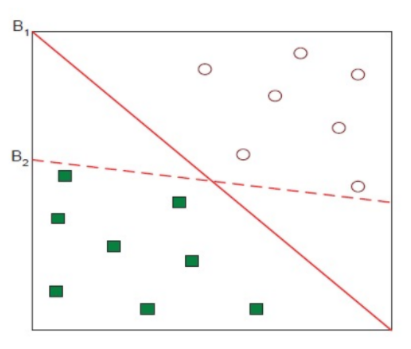
⇒ B1이 더 좋음!!
⇒ How do you define better? → defined the margin
점과 선 사이의 거리
-
점 (x1,y1)과 선 ax+by+c=0
d=a2+b2∣ax1+by1+c∣
-
점 (x1,y1,z1)과 평면 ax+by+cz+d=0
d=a2+b2+c2∣ax1+by1+cz1+d∣
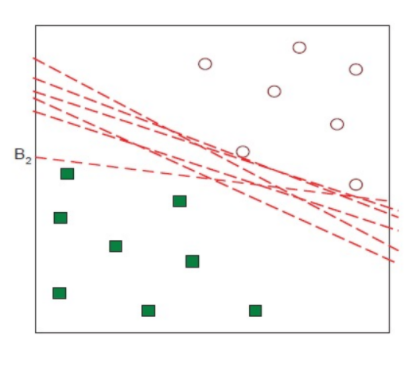
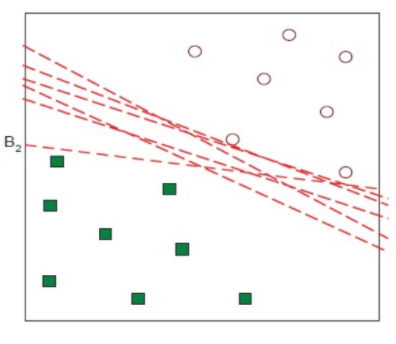
Margin
-
Distance from example x to the seperator is
r=∣∣w∣∣wTx+b
-
margin이 가장 큰 hyperplane 선택
-
가장 가까운 hyperplane ⇒ support vector
-
separator의 Margin ρ는 classes 사이의 separation의 width 값
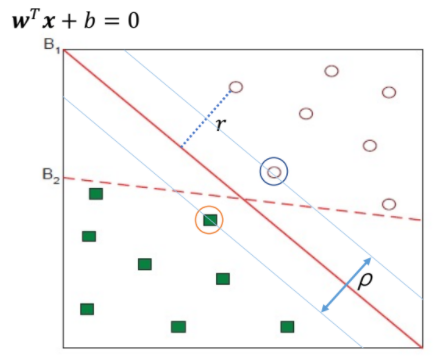
Maximum Margin Classification
-
Margin을 최대화하는 것은 직관에 따라 좋으며, 아마 거의 정확한(PAC, probably approximately correct) 이론
-
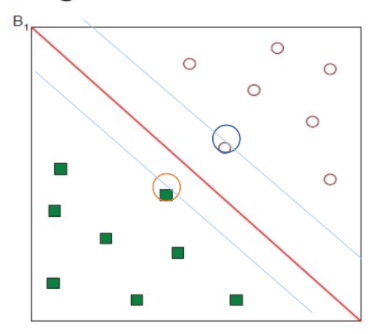
오직 support vector만 중요하며 다른 training examples는 무시해도 됨
⇒ support vector 2개만 남겨놓고 나머지는 버림
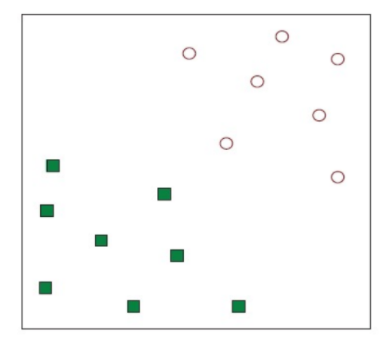
💡 Linear separable 하지 못한 예시는?
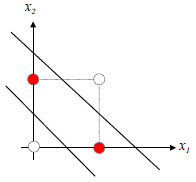
⇒ 대표적인 예 : XOR 문제
Linear SVMs Mathematically
- 모든 data의 거리(functional margin)가 적어도 1이라고 가정
- 적어도 하나의 data가 1과 같다고 가정
-
제약 조건 (training set {(xi,yi)})
wTx+b≥1 if yi=1
wTx+b≤−1 if yi=−1
-
주어진 data를 학습하는 것은 w를 찾는 것과 같음 ❗
⇒ margin이 가장 큰 w를 찾아야 함
단, 제약 조건을 만족해야 함
-
Margin ρ
ρ=∣∣w∣∣2
💡 최적화 문제
최적화 문제는 보통 최소화하는 문제이지만 우리는 margin을 최대화하는 게 목적임
⇒ 원래 margin에 역수를 취해서, 2∣∣w∣∣가 최소가 되도록 하는 ||w||를 찾기
(단, 제약조건을 만족하면서)
- 21wTw는 Quadratic function (2차 함수)
yi(wTx+b)≥1는 Linear (선형)
📌 Quadratic programming
- 목적함수가 이차 함수이며, 제약조건이 선형일 때 최적화하는 문제
- Lagrange multiplier(라그랑주 승수법)을 사용하여 해결할 수 있음
Constrained Optimization
📌 Equality constraints - Lagrange multiplier
-
f(x1,x2,...,xd)에 대한 제약조건 gi(x)=0, i=1,2,...,p
⇒ 제약조건이 여러 개(p개)일 수도 있음!
-
라그랑주 승수법
Lagrangian 정의
L(x,λ)=f(x)+∑i=1pλigi(x)
⇒ λi는 dummy variable(가변수)로 Lagrange multiplier
⇒ 모든 constraint에 대해서 λ 를 곱하고 더하며, constraint가 n개 있으면 λ도 n개 있음!
- 미분 수행
∂xi∂L=0, ∀i=1,2,...,d
∂xi∂L=0, ∀i=1,2,...,p
⇒ d : x 개수
⇒ p : constraint 개수
📝 Example
-
f(x,y)=x+2y를 최소화
-
constraint : x2+y2−4=0
-
Lagrangian 정의
L(x,y,λ)=x+2y+λ(x2+y2−4)
-
미분 수행
∂x∂L=1+2λx=0
∂y∂L=1+2λy=0
∂λ∂L=x2+y2−4=0
-
결과
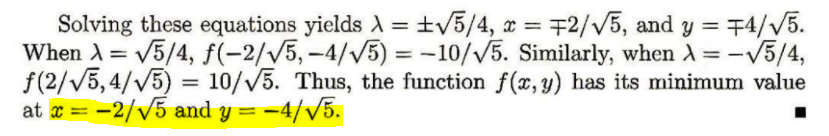
📌 Inequality constraints - KKT
-
f(x1,x2,...,xd)에 대한 제약조건 hi(x)≤0, i=1,2,...,q
-
Lagrangian
L=f(x)+∑i=11λihi(x)
-
다음과 같은 제약조건을 만족해야함 (Karush-Kuhn-Tucker 조건 (KKT))
∂xi∂L=0, ∀i=1,2,...,d
hi(x)≤0, ∀i=1,2,...,q
λi≥0, ∀i=1,2,...,q
λihi(x)=0, ∀i=1,2,...,q
-
KKT 조건을 직접 푸는 건 어려움
📝 Example
-
f(x,y)=(x−1)2+(y−3)2 를 최소화
-
constraint : x+y≤2, and y≥x
⇒ x+y−2≤0,x−y≤0
-
Lagrangian 정의
L=(x−1)2+(y−3)2+λ1(x+y−2)+λ2(x−y)
-
KKT 제약조건
∂x∂L=2(x−1)+λ1+λ2=0
∂y∂L=2(y−3)+λ1−λ2=0
λ1(x+y−2)=0
λ2(x−y)=0
λ1≥0,λ2≥0,x+y≤2,y≥x
💡 Case 1: λ1=0,λ2=0
2(x−1)=0
2(y−3)=0
x = 1, y= 3이므로 제약조건 x+y≤2 만족 X
💡 Case 2: λ1=0,λ2=0
x−y=0
2(x−1)+λ2=0
2(y−3)−λ2=0
x = 2, y = 2, λ_2 = -2이므로 제약조건 λ2≥0,x+y≤2 만족 X
💡 Case 3: λ1=0,λ2=0
x+y−2=0
2(x−1)+λ1=0
−2(x+1)+λ1=0
x = 0, y = 2, λ_1 = 2이므로 제약조건 만족 ❗
💡 Case 4: λ1=0,λ2=0
x+y−2=0
x−y=0
2(x−1)+λ1+λ2=0
2(y−3)+λ1−λ2=0
x = 1, y = 1, λ_1 = 2, λ_2 = -2이므로 제약조건 만족 X
Cont'd
💡 그럼 이제 우리한테 주어진 문제를 풀어보자!

-
Lagrangian 정의
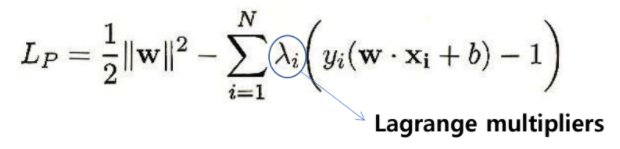
-
Karush-Kuhn-Tucker (KKT) conditions

- dual problem
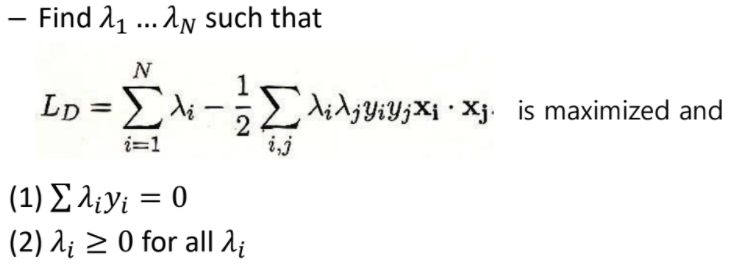
-
w=∑λiyixi, b=yk−wTxk
-
λ의 대부분이 0 값을 가지며, λ가 0이 아닌 데이터들이 support vector가 됨!
-
새로운 data f(x)=∑λiyixiTx+b
-
xiTxj 중요 ❗