이 글은 [파이썬과 케라스로 배우는 강화학습]을 기반으로 작성되었습니다.

시작하며

지난 포스팅 에서는 MDP와 벨만방정식에 대해 다루었습니다. 이번 포스팅에서는 벨만 방정식을 계산으로 풀어 순차적 의사결정 문제를 해결하는 다이나믹 프로그래밍에 대해 다루겠습니다.

다이나믹 프로그래밍

지난 포스트에서 벨만 방정식을 풀어내는 것이 강화학습의 과제라고 했습니다. 다이나믹 프로그래밍은 벨만 방정식을 이용해 MDP로 정의되는 순차적 의사결정 문제를 "계산"으로 풀어냅니다. 그리고 이 다이나믹 프로그래밍의 한계를 극복하고자 도입되었던 것이 강화학습입니다.

다이나믹 프로그래밍은 1953년 리처드 벨만에 의해 소개되었습니다. 다이나믹 프로그래밍의 기본적인 아이디어는 큰 문제 안에 작은 문제들이 중첩된 경우에 전체 큰 문제를 작은 문제로 쪼개서 풀겠다는 것입니다. 그리고 작은 문제의 해답을 서로 이용하는 것입니다. 이를 MDP에 도입하면, 가치함수를 구하는 과정을 한 번에 구하는 것이 아니라 작은 과정으로 쪼개서 반복적으로 계산하는 것이라고 이해할 수 있습니다. 즉 iteration을 도입해 여러 번에 나눠서 가치 함수를 풀어나갑니다.

다이나믹 프로그래밍에는 정책 이터레이션과 가치 이터레이션 두 가지 방법이 있습니다. 정책 이터레이션은 벨만 기대방정식을 이용해 문제를 풀고 가치 이터레이션은 벨만 최적방정식을 이용해 문제를 풉니다.

정책 이터레이션

정책은 에이전트가 모든 상태에서 어떻게 행동할지에 대한 정보입니다. 우리는 MDP로 정의되는 문제를 푸는 것을 통해서 가장 높은 보상을 얻게 하는 정책을 찾아야 합니다. 하지만 처음에는 보상도, 최적의 정책도 알 수가 없으므로 처음에는 무작위로 행동을 정하는 정책에서부터 시작하여 점점 발전시켜나가는 방법을 사용합니다. 이를 정책 이터레이션이라 합니다.

정책 이터레이션을 진행하며 정책을 바꿔나가기 위해서는, 현재 정책을 평가하고 이를 바탕으로 발전을 시켜야 합니다. 따라서 정책 평가와 정책 발전의 개념이 도입됩니다.

정책 평가

정책을 어떻게 평가할 수 있을까요? 정책 평가의 근거는 가치함수입니다. 다이나믹 프로그래밍의 핵심은, iteration을 도입해 여러 번에 나눠서 가치 함수를 풀어나가는 것이라고 말씀 드렸었습니다. 즉, 정책 이터레이션은 벨만 기대 방정식을 사용해 여러 번에 나눠서 가치 함수를 풀어나가고, 이를 바탕으로 정책을 발전시키는데, 핵심은 주변 상태의 가치함수와 한 타임스텝의 보상만 고려해서 현재 상태의 다음 가치함수를 계산하는 것 입니다. 그리고 이를 반복하는 것 입니다.

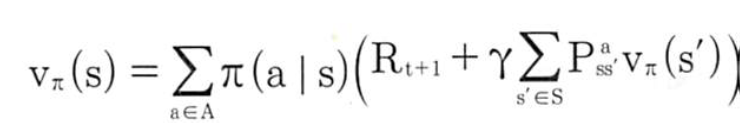
지난 포스팅에서 언급했던 계산 가능한 벨만 방정식의 형태입니다. 이 수식에서 상태변환확률을 1이라고 가정하면(앞으로 간다는 행동을 취했을 때 실제로 앞으로 갈 수 있는 확률이 100%라고 가정) 수식은 다음과 같이 변형됩니다. grid world 같은 예제에서는 상태변환확률이 1이라고 할 수 있습니다.

vπ(s) = Σπ(a|s)(Rt+1 + γvπ(St+1) | St = s ]

다이나믹 프로그래밍의 정책 평가는 π라는 정책에 대해 반복적으로 수행되며, 정책 평가에 따라 반복적인 정책 발전이 이루어져야 합니다. 따라서 계산의 단계를 표현하기 위해서 k 변수를 식해 추가합니다. k번째 가치함수를 통해 k+1번째 가치함수를 계산하는 식은 아래 수식과 같습니다.

vk+1(s) = Σπ(a|s)(Rt+1 + γvk(St+1) | St = s ]

이 수식으로 가치 함수를 평가할 수 있습니다. 그런데 위 수식을 풀어내려면, 수식에서도 확인할 수 있듯 에이전트는 다음 상태 St+1의 현재단계(k)의 가치함수를 이용해야 합니다. 즉, grid world 예제에서 상, 하, 좌, 우 4가지의 행동이 가능하다고 했을 때, vk+1(s) = Σπ(a|s)(Rt+1 + γvk(St+1) | St = s ] 의 수식을 계산하려면 각 행동을 취했을 때 도달할 상태의 가치함수 값 4가지를 이용해야 합니다.

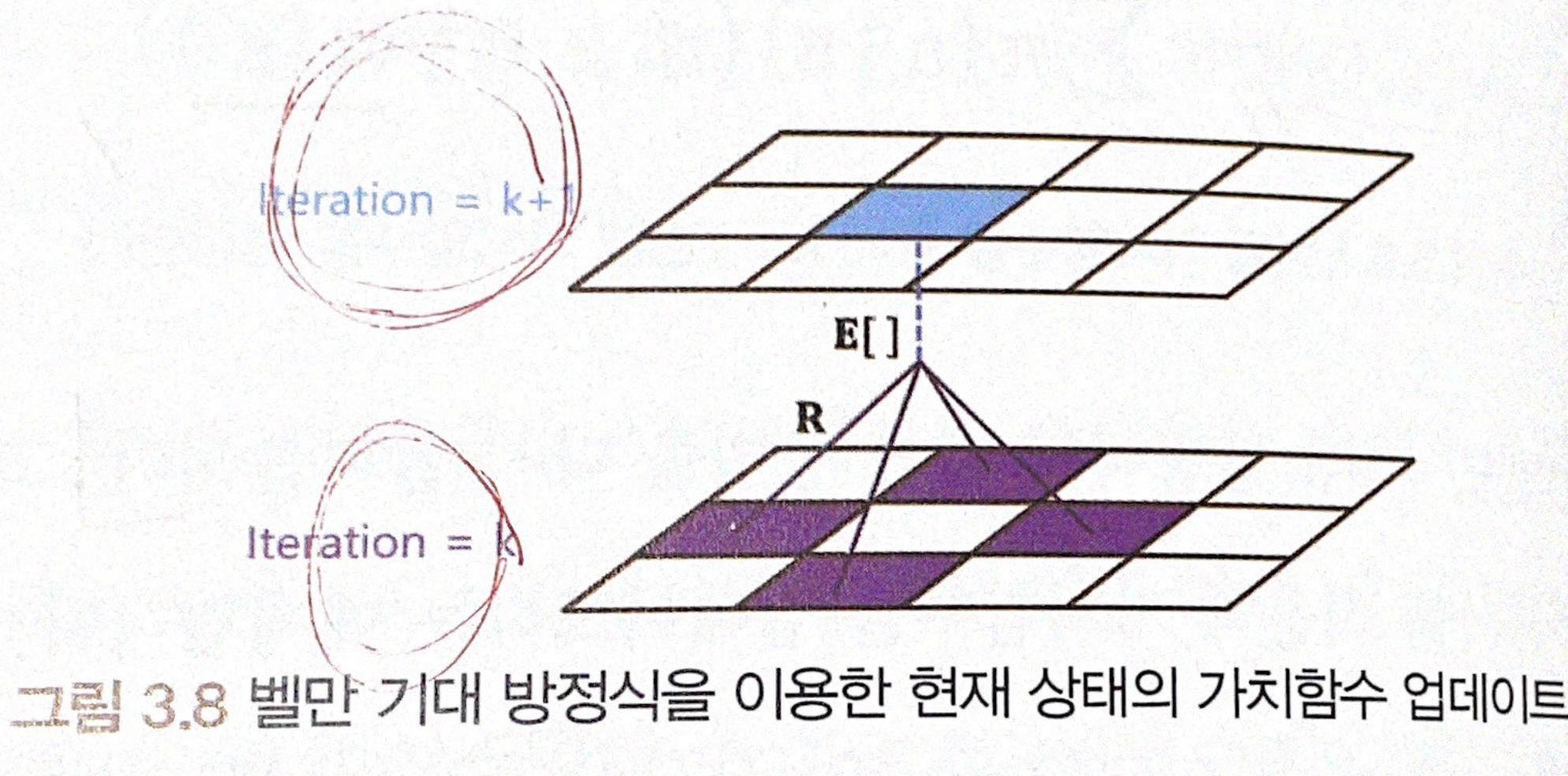
이를 그림으로 표현하면 위와 같습니다. iteration k+1 단계의 가치함수 행렬에서 현재 상태(하늘색)의 가치함수 vk+1(s)는 iteration k 단계의 다음 상태(보라색)의 가치함수를 고려해서 계산하게 됩니다.

정책 발전

정책 평가를 마쳤다면 정책을 발전시켜야 할 것입니다. 정책 발전의 방법은 정해져 있는 것은 아니지만, greedy policy improvement(탐욕 정책 발전)이 가장 널리 알려져 있습니다. 탐욕 정책 발전의 개념은 간단합니다. 선택 가능한 행동 중 가장 큰 가치를 가지는 행동을 선택하는 것입니다. 즉, 상태 s에서 선택 가능한 행동의 큐함수들을 모두 비교하고 그 중에서 가장 큰 큐함수를 가지는 행동을 선택하면 됩니다. 탐욕 정책 발전으로 업데이트하게 되는 새로운 정책 π'(s)는 다음과 같습니다.

π'(s) = argmaxa∈AQπ(s,a)

greedy를 통해 정책을 업데이트하면 이전 가치함수에 비해 업데이트된 정책으로 움직였을 때 받을 가치함수가 무조건 크거나 같게됩니다. 이런 식으로 정책을 업데이트해 최적 정책에 수렴하려는 방법을 다이나믹 프로그래밍의 정책 이터레이션이라고 합니다.

가치 이터레이션

가치 이터레이션은 현재의 가치함수가 최적은 아니지만, 최적이라고 가정합니다. 물론 처음의 가치함수가 최적이 아니므로 최적 정책의 형태를 가정하는 것은 틀린 가정일 것입니다. 하지만 반복적으로 가치함수를 발전시키기 때문에 결국 최적에 도달하는데, 이를 가치 이터레이션이라고 부릅니다. 가치 이터레이션에서는 '정책 발전'의 개념이 필요가 없습니다. 정책의 발전은 설명하지 않고 오직 가치함수만 업데이트를 시킵니다. 정책은 이미 가치함수 안에 내재되어 있으므로, 가치함수를 업데이트하면 자동적으로 정책 역시 발전된다고 가정합니다.

벨만 기대 방정식을 이용하는 정책 이터레이션과 다르게 가치 이터레이션은 벨만 최적 방정식을 이용합니다.

maxE[Rt+1 + γv*(St+1) | St = s, At = a]

최적 방정식을 계산함을 통해 나오는 v*(s)값은 최적 가치함수입니다. 가치함수를 최적 정책에 대한 가치함수라고 가정을 하고, iteration을 돌려 반복적으로 계산을 하게 되면, 최적 정책에 대한 참 가치함수인 '최적 가치함수'를 찾을 수 있다는 것이 바로 가치 이터레이션의 아이디어 입니다.

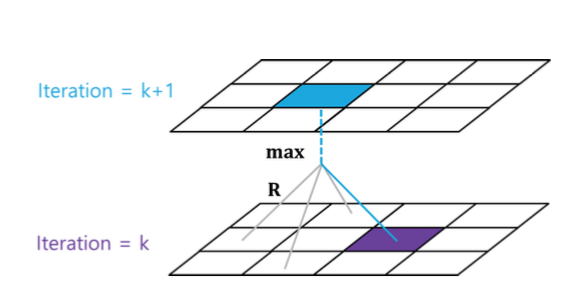
최적 방정식 수식에서도 볼 수 있듯, 가치 이터레이션은 max를 취하기 때문에 현재 상태에서 가능한 Rt+1 + γvk(St+1) 중에 최고의 값으로 업데이트만 하면 됩니다. 정책 이터레이션에서 가치함수를 업데이트 할 때에는 각 행동을 취했을 때 도달할 상태의 가치함수 값 4가지 모두를 이용해야 했지만, 가치 이터레이션에서는 최고 값으로만 업데이트하면 됩니다.

따라서 계산 가능한 벨만 최적 방정식은 다음과 같습니다.

vk+1(s) = maxa∈A(r(s,a)+γvk(s'))

즉, 기대 방정식을 이용하는 정책 이터레이션과 달리 최적 방정식을 이용하는 가치 이터레이션을 쓰면 max를 취하기 때문에 새로운 가치함수를 업데이트할 때 정책값을 고려해줄 필요가 없을 뿐더러 다음 상태들을 다 고려할 필요도 없고 제일 높은 값을 가지는 값 하나로만 업데이트해주면 됩니다. 이것이 가치 이터레이션의 주요 포인트입니다.

다이나믹 프로그래밍의 한계

그러나 정책 이터레이션과 가치 이터레이션으로 대표되는 다이나믹 프로그래밍에는 분명한 한계점이 존재합니다. 이러한 한계점으로 인해 강화학습의 필요성이 대두되었습니다. 다이나믹 프로그래밍의 한계점은 다음과 같습니다.

1. perfect model을 알아야한다.
2. 계산 복잡도가 높다.
3. 상태의 차원이 늘어날수록 상태 수가 기하급수적으로 늘어나는 차원의 저주 문제가 존재한다.

특히 1번 문제점이 중요한데, 다이나믹 프로그래밍은 보상과 상태 변환 확률을 정확히 안다는, 즉, 환경을, 모델을 안다는 가정 하에 풀 수 있습니다. 그런데 보통은 이 정보를 정확히 알 수 없기 때문에, 현실 세계의 문제를 풀 때에는 이 한계가 치명적으로 작용합니다. 따라서 model-free의 필요성이 대두되고, 환경은 모르지만 환경과의 상호작용을 통해 학습하는 방법, 즉 강화학습이 등장하게 됩니다.

다음 포스팅

다음 포스팅에서는 모델 없이 학습하는 강화학습의 기본 알고리즘에 대해서 포스팅 하겠습니다. 자세히는 몬테카를로 예측, 시간차 예측, 강화학습 알고리즘 SARSA와 Q-learning에 대해 다룹니다.