Section 5_Sprint 1

JIYOUNG KIM·2022년 3월 28일

section5 코드스테이츠

Codestates AIB

목록 보기

13/15

Day 1

python Programming

정규표현식, re

re.search()
- 문자열 처음부터 일치하지 않아도 됨
- ctrl+f 느낌
re.match()
- 문자열 처음부터 일치해야 함
re.match().span()
re.match().group()
- 매치된 문자열 취득
re.match().groups()
- 각 그룹의 문자열 취득
re.complie()
- 정규표현 패턴 문장열을 컴파일하여 정규표현 패턴 오브젝트를 작성할 수 있음
re.VERBOSE
- 정규표현식이 더 읽기 편하게 만들어 줌
string 앞에 0을 채우는 방법
1. rjust(width, [fillchar])
```
str = "123"
str.rjust(5, "0")
# 00123

"123".rjust(5, "a")
# aa123
```
2. zfill(width)
  - rjust() 와 달리 0으로만 채우는 것
print('raw string을 사용하지 않고고\b 문자 출력하기')
→ raw string을 사용하지 않고 문자 출력하기
print(r'raw string을 사용하지 않고고\b 문자 출력하기')
→ raw string을 사용하지 않고고\b 문자 출력하기
map(function, iterable)
- iterable : 리스트, 튜플 등 반복 가능한 자료형
filter(function, list)
- 리스트에 들어있는 원소들을 함수에 적용시켜서 결과가 참인 값들로 새로운 리스트를 생성
```
list(filter(lambda x: x<5, range(10)))
# [0,1,2,3,4]
```
reduce(function, sequence)
- 시퀀스(문자열, 리스트, 튜플)의 원소들을 누적적으로 함수에 적용
```
reduce(lambda x, y: x+y, [0,1,2,3,4])
# 10
# 0+1=1, 1+2=3, 3+3=6, 6+4=10
```
얕은 복사 & 깊은 복사 & 단순할당
- 얕은 복사 : a.copy() = a[:] 와 깊은 복사 : deepcopy() 는 메모리 위치가 다름
  - a[0], b[0] 의 메모리의 위치는 얕은 복사는 같지만 깊은 복사는 다름
- 단순할당 : a=b 는 메모리 위치가 같음
- https://pinkwink.kr/1234
메타문자

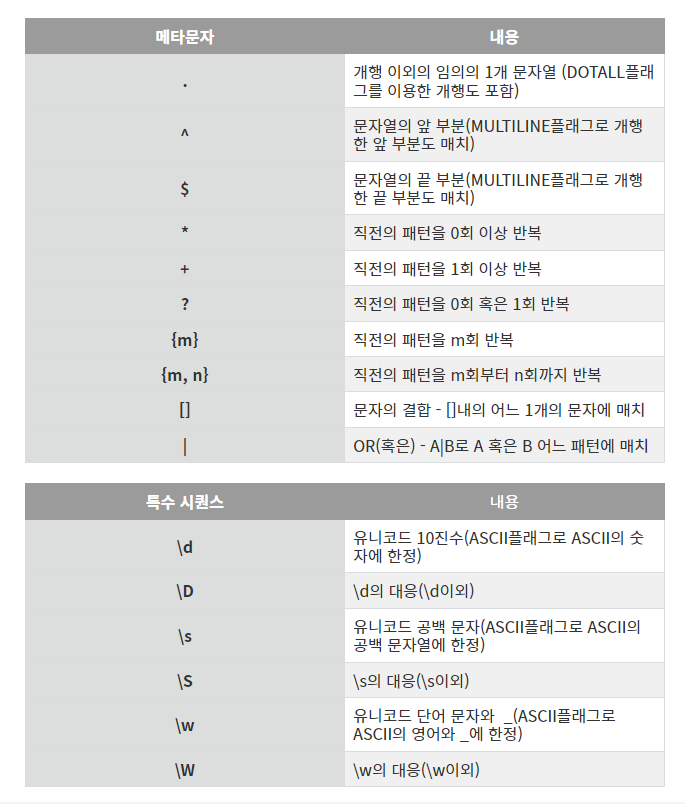
정규표현식 정리
https://hamait.tistory.com/342

Day 2

Problem Solving

Comprehension

List Comprehension
[반복실행문 for 반복변수 in 반복범위 if 조건 else 조건외]
Set Comprehension
{반복실행문 for 반복변수 in 반복범위 if 조건 else 조건외}

Dictionary Comprehension
{키:밸류 for 반복변수 in 반복범위 if 조건 else 조건외}

names = ['amy', 'jane', 'sophia', 'jay']
scores = [7, 9, 5, 10]
pas = []
for name, score in zip(names, scores):
    if score > 8:
        pas.append('PASS')
    else:
        pas.append('NO PASS')

# 컴프리헨션으로 표현
pas = ['PASS' if score > 8 else 'NO PASS' for name, score in zip(names, scores)]

scores = [7, 9, 5, 10]
ans = []

for score in scores:
    arr = ['no pass', 'pass']
    ans.append(arr[score > 8])
    
# 컴프리헨션으로 표현
pas = [['no pass','pass'][score > 8] for name, score in zip(names, scores)]

지역변수와 전역변수

지역변수 : 해당 변수가 포함된 함수 안에서만 수정하고 읽을 수 있음
- 이름이 같더라도 소속된 함수가 다르면 다른 변수로 취급
일반 전역변수 : 하나의 파이썬 파일전체에서 값을 읽을 수 있음
- global 전역변수 : 변수가 생성되는 시점이 일반 전역변수와 다름
  
  전역변수 문제점
  https://codingcoding.tistory.com/361

예외처리

try ~ except
try ~ except ~ else
try ~ except ~ finally
- 오류 발생 유무와 관계없이 특정 코드를 무조건 실행시키려 할 때
사용자 정의 예외처리
- raise Exception('안내문구')
- assert 조건식, 조건식이 False인 경우 출력되는 메세지
  - 조건식이 False : AssertionError 예외 발생
  - 조건식이 True : 어떠한 메시지도 표시되지 않음

의사코드 작성법
https://42kchoi.tistory.com/114

리스트명.sort() : 리스트형의 메소드, 리스트 원본값 직접 수정
sorted(리스트명) : 내장함수, 리스트 원본값은 그대로, 정렬값을 반환

Day 3

Python with OOP

OOP : Object Oriented Programming, 객체지향 프로그래밍

실체가 있는 모든 물체를 클래스와 인스턴스, 함수, 변수라는 object로 변화시켜서 프로그램을 구성
기본 전제: 기능(함수, 변수) 재사용이 가능하도록 설계 및 프로그래밍 했는지
OOP의 개념을 무분별하게 활용하면 유지보수가 어려워 질 수 있어 설계방향 및 서비스 기능에 따라 사용해야 함
data-driven(데이터기반 의사결정), 컴퓨터 하드웨어 성능, 데이터양 증가에 따라 OOP 활용 증가

OOP의 구성

캡슐화
- 내부 속성(변수)과 함수를 하나로 묶어서 클래스로 선언
상속과 포함
- 상속(Inheritance) : 상위 클래스의 모든 기능(함수, 변수)을 재사용할 수 있음
- 포함(Composition) : 다른 클래스의 일부 기능(함수)만을 재사용
추상화
- 복잡한 내용에서 핵심적인 개념 및 기능을 요약하는 것
- object의 기능에 따라 추상클래스(상위클래스)를 상속받아 개별적으로 클래스(하위클래스)를 생성
- 기본적으로 추상메소드를 선언하며 실제 실행되는 기능은 보여지지 않음
  - 실제 실행되는 기능은 선언된 추상클래스는 상속 받은 다른 클래스의 메소드에서 확인 가능
다형성
- 계층 구조의 상속관계에서 상속받은 기능 외, 다른 기능을 추가적으로 제공하고자 할 때 사용
- 구현되는 하위클래스에 따라 클래스를 다르게 처리하는 기능
- 상속과 달리 상위클래스의 기능을 그래도 재사용하는 것은 아님
- 장점
  - 프로그램 작성 코드량 줄여줌 → 잘 쓰면 if/else 문 줄일 수 있음
  - 코드의 가독성 높여줌

연산자 1개(is not) : A는 B가 아니다.
foo = ''
if foo is no None: # 한 번만 해석하면 됨
   print('가독성 좋음') 
연산자 2개(not, is) : A가 아닌것은 None이다.
if not foo is None: # 두 번 해석해야 함
   print('가독성 좋지 않음')

Programmatic Design

클래스 설계
- 코드 재사용
클래스의 인스턴스화
- 클래스를 생성했으면, 이를 활용하기 위한 인스턴스 필요
- object가 생성된 후 object가 소프트웨어의 메모리에 할당되면 인스턴스가 되는 것
  - object는 인스턴스를 포함할 수 있고 포괄적 의미를 가짐
```
class MyFirstClass:
   pass
a = MyFirstClass() # 인스턴스화(메모리할당됨)

print(a) # 주소값은 일반적인 정수값과 다르게 나옴
```
모듈
- 파이썬에서 코드가 저장된 파일
- 모듈을 활용하면 유지보수가 쉬운 프로그램 작성 가능
- 모듈 불러오는 방법
  - import 모듈명
  - from 모델명 import 변수/함수/클래스명
  - from 모듈명 import *
메소드 오버라이딩
- 상속처럼 부모클래스의 메소드를 재호출하는 것이 아니라 같은 이름의 메소드를 신규 생성하는 것
- 다형성 개념의 한 종류

enumerate
반복문 사용 시 몇 번째 반복문인지 확인 가능
인덱스 번호화 컬렉션의 원소를 튜플형태로 반환

Q & A

파이썬의 자료형은 하나의 클래스
a.split() 은 문자열에서 사용 가능
객체지향
- 어떤 프로그래밍 방식(방법론) → 프로그래밍을 더 쉽고 더 잘하기 위해 사용
클래스
- 현실에 있는 사물을 정의
- 클래스를 사용할 때 가장 큰 이점
  - 유지보수 간편 → 대규모 프로그램 개발 가능
  - 상속기능 이용
    - 클래스들끼리 기능 물려주는 것
    - 부모클래스 --(기능)--> 자식클래스
    - 부모의 기능을 자식 클래스에 코딩하지 않아도 됨
객체
- 속성(상태, 특징)과 행위(행동, 동작, 기능)로 구성된 대상
- 속성은 변수로, 행동은 함수로 구현
- 객체를 만들고 이용할 수 있는 기능을 제공하는 프로그래밍 언어를 객체지향 프로그래밍 언어라 함
- 객체를 만들려면 먼저 클래스 선언해야 함
- 클래스는 객체의 공통된 속성과 행위를 변수와 함수로 정의한 결과
  - 클래스 : 객체를 만들기 위한 기본 틀
  - 객체 : 기본 들을 바탕으로 만들어진 결과, 클래스의 인스턴스라함

클래스 구조

# 클래스 선언
class 클래스명():
    실행코드
    # self : 객체 생성한 후 자신을 참조하는데 이용
    def 함수명(self, 여러가지 인자들):
       실행코드
       
# 객체 선언
객체명 = 클래스명()

# 객체의 메소드 호출
객체명.메소드명()

# 클래스 선언
 class Car():
 pass

# 선언된 클래스로부터 객체 생성
my_car = Car()

# 객체에 속성값 설정
my_car.color = 'red'

# 객체에 속성값을 가져와서 출력
print('차 색상:', my_car.color)

# 클래스를 선언할때 초기화 함수 사용하면 객체를 생성하는 것과 동시에 속성값을 지정 할 수 있음
class Car():
   def __init__(self, color):
       self.color = color

my_car = Car('black')
print('차 색상:', my_car.color)

객체 초기화
__init__() 함수는 클래스의 인스턴스가 생성될 때 자동으로 실행되기 때문에 __init__() 함수에 초기화하려는 인자를 정의하면 객체를 생성할 때 속성을 최기화할 수 있음

클래스에서 사용되는 변수

클래스 변수는 클래스 내에 있지만 함수 밖에서 변수명=데이터 형식으로 정의한 변수로 클래스에서 생성한 모든 객체가 공통으로 사용가능, 클래스명.변수명 형식으로 접근 가능

인스턴스 변수는 클래스 내의 함수 안에서 self.변수명=데이터 형식으로 정의한 변수로서 클래스 내의 모든 함수에서 self.변수명 으로 접근 가능

# 클래스 선언
class Car():
    pass

# 선언된 클래스로부터 객체 생성
my_car = Car()

# 객체에 속성값 설정
my_car.color = 'red'

# 객체에 속성값을 가져와서 출력
print('차 색상:', my_car.color)

# 클래스를 선언할때 초기화 함수 사용하면 객체를 생성하는 것과 동시에 속성값을 지정 할 수 있음
class Car():
   def __init__(self, color):
       self.color = color

my_car = Car('black')
print('차 색상:', my_car.color)

# 클래스명 Card를 통해 my_card1, my_card2, my_card3 만들고 3개의 카드 balance 가 모두 10000가 출력되게

# 클래스 선언
class Card():
   def __init__(self):
       self.balance = 10000

my_card_1 = Card()
my_card_2 = Card()
my_card_3 = Card()

# 객체 3개 선언

# 객체 속성값 가져와서 출력
print(my_card_1.balance)
print(my_card_2.balance)
print(my_card_3.balance)

# 총 발급된 카드 수가 3이 나오도록
class Card():
   issued_card_count = 0
   def __init__(self):
       self.balance = 10000
       Card.issued_card_count += 1

my_card_1 = Card()
my_card_2 = Card()
my_card_3 = Card()

print('총 발급된 카드 수:', Card.issued_card_count)

함수에서 어떤 변수를 호출하면 지역 영역, 전역 영역, 내장 영역 순서로 변수가 있는지 확인

Day 4

Data Structure Essential

자료구조의 배경

대용량의 다양한 데이터를 효율적으로 처리(저장)하기 위해 개발
배열
- 각각의 변수를 하나의 변수에 여러 개의 인덱스로 묶는 것
  - arr[5]
- 파이썬에서는 배열을 리스트와 튜플로 구현 & 활용
  - 리스트 자료형이 자료구조의 연결리스트로 역할

자료구조와 효율성

Big O 표기법(notation)
- 알고리즘 효율 확인 가능
  - 해당 코드가 얼마나 수행되었는지(결과값을 출력하기 위한 연산을 얼마나 반복하였는지)에 따라 효율성 확인
- 데이터 입력값 크기에 따라 알고리즘 실행 속도의 변화를 설명하는 방법
- 알고리즘 계산 복잡도 종류
  - 시간 복잡도 : 알고리즘을 활용해 얼마나 실행시간이 걸렸는지
  - 공간 복잡도 : 문제해결을 위해 얼마만큼 메모리 저장 공간이 필요한지
    - 하드웨어의 성능이 증가하면서 공간 복잡도보다 소프트웨어 성능인 시간 복잡도가 더 중요
- Big O 표기법(O(n))만으로 성능 예측 X
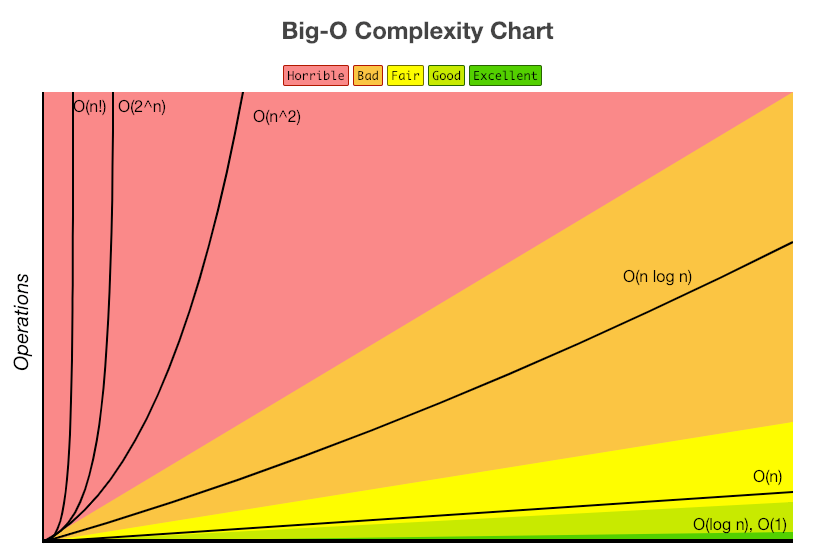
- 0(1) - 상수시간(Constant): 문제를 해결하는 데 오직 한 단계만 처리
- (log n) - 로그시간(Logarithmic) : 문제를 해결하는 데 필요한 단계들이 연산마다 특정요인에 의해 줄어듬
- 0(n) - 선형시간(Linear) : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐
- 0(nlogn) - 선형로그시간(Linearithmic) : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큰의 수행시간을 가짐
- 0(n^2) - 2차시간(Quadratic) : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱
- 0(c^n) - 지수시간(Exponential) : 문제를 해결하기 위한 단계의 수는 주어진 상수값 c의 n제곱
  - 시간복잡도를 확인할 때 우선적으로 고려할 것은 반복문으로 반복문이 한번 수행되면 0(n)이 될 수 있고, 반복문이 중첩해서 2개가 수행되면 0(n^2)이 될 수 있음 → 입력출력값 로직에 따라 달라질 수 있음

Q & A

자료구조
- 자료를 쉽게 관리하기 위해 다양한 구조로 묶은 것
알고리즘
- 컴퓨터에 지시하는 처리 절차
- 그 처리의 대상이 되는 것이 데이터
- 데이터의 처리를 실시하는 가장 기본적인 구조 : 변수
- 데이터가 메모리에 저장되어서 사용됨
데이터는 메모리에 저장
- 데이터 입력 / 데이터 가공 / 데이터 출력
  → 과정을 거치는 동안 데이터는 메모리라는 장치에 저장
  - 컴퓨터는 알고리즘에서의 처리 명령에 따라 메모리에서 데이터를 꺼내 가공한 후 메모리에 저장하는 작업을 반복
복잡도
- 시간 복잡도 : 얼마나 빠르게 실행되는지
  - 빠르고 느린지는 시간보다는 단계가 얼마나 있는지, 적은 단계로 복잡도를 줄여 성능을 높이는 것을 목표로 함
- 공간 복잡도 : 얼마나 많은 저장공간이 필요한지
- 좋은 알고리즘 = 실행시간이 짧고 저장공간도 적게 쓰는 알고리즘
  → 둘다 만족 시킬 수 있을까? N(시간과 공간은 반비례)
  → 보편적으로 시간복잡도 우선시해서 프로그램 작성

JIYOUNG KIM

데이터분석가

이전 포스트

Section 4_Sprint 3

다음 포스트

Section 5_Sprint 1

Codestates AIB

Day 1

python Programming

정규표현식, re

Day 2

Problem Solving

Comprehension

지역변수와 전역변수

예외처리

Day 3

Python with OOP

OOP : Object Oriented Programming, 객체지향 프로그래밍

OOP의 구성

Programmatic Design

Q & A

Day 4

Data Structure Essential

자료구조의 배경

자료구조와 효율성

Q & A

Section 4_Sprint 3

Section 5_Sprint 2

0개의 댓글