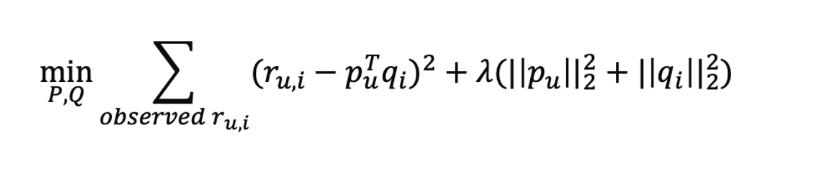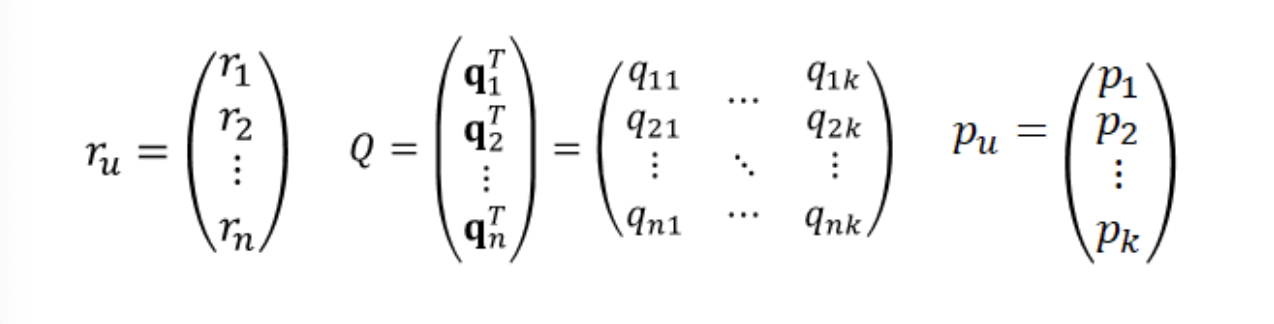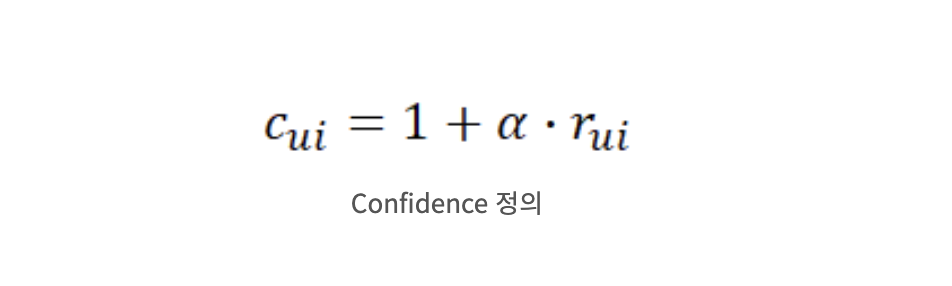Least Square Method, ALS 수식 증명

Least Square Method

• Wikipedia
  최소 제곱법(Least Square Method)은 데이터의 잔차(Residual) 제곱합을 최소화하는 모수(Parameter)를 추정하는 방법입니다.

• 특히 선형 회귀 분석(linear regression analysis)에서 많이 사용된다.

• 오차(Noise)가 가우시안 분포를 따른다는 가정 하에, 최적의 예측값(Predicted Value)을 추정할 수 있습니다.

• 데이터셋에서 빠르게 계산할 수 있으며, 이를 통해 큰 규모의 데이터셋에서도 적용할 수 있습니다.

The goal is to find the parameter values for the model that "best" fits the data.

$r_{i}=y_{i}-f\left(x_{i}, \boldsymbol{\beta}\right)$

• Residual : 타겟값 - 예측값

$S=\sum_{i=1}^{n} r_{i}^{2}$

• the sum of squared residuals

The least-squares method finds the optimal parameter values by minimizing the sum of squared residuals.

$\frac{\partial S}{\partial \beta_{j}}=2 \sum_{i} r_{i} \frac{\partial r_{i}}{\partial \beta_{j}}=0, j=1, \ldots, m$

and since $r_{i}=y_{i}-f\left(x_{i}, \boldsymbol{\beta}\right)$, the gradient equations become

$-2 \sum_{i} r_{i} \frac{\partial f\left(x_{i}, \boldsymbol{\beta}\right)}{\partial \beta_{j}}=0, j=1, \ldots, m$

• The minimum of the sum of squares is found by setting the gradient to zero. Since the model contains m parameters, there are m gradient equations.
  미분한 값이 0이 되도록 학습하면 된다.

데이터를 각각의 모델에 맞게 적합시킨 결과

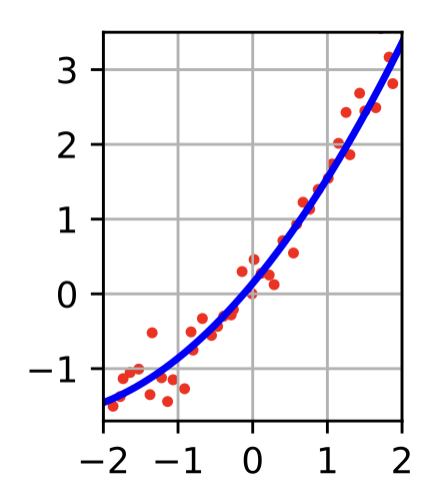
• 2차 함수
  
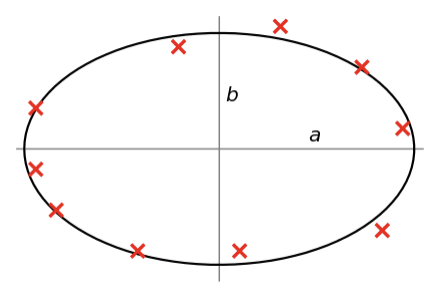
• 타원형

• PLUS
  f(x)가 2차 함수, 타원 등.. 어떤 형태가 주어지고
  만약 y=ax^2+bx+c가 f(x)라면 a,b,c를 찾는 것을 의미한다.

• 추천 시스템에서 최소 제곱법(Least Square Method)
  사용자의 구매 기록이나 평가 데이터를 토대로 상품의 특성과 사용자의 취향을 분석하여 상품 추천을 제공하는 데 사용될 수 있다.
  예측 값이 사용자가 아직 구매하지 않은 상품에 대한 사용자의 선호도라고 가정하면 아직 구매하지 않은 상품에 대한 예측 값을 계산할 수 있습니다.

예를 들어, 영화 추천 시스템에서는 영화 제목, 배우, 감독, 장르 등의 특성을 상품 변수로, 사용자의 선호도를 나타내는 변수로는 영화에 대한 평가나 시청 기록 등을 사용할 수 있습니다.
이후, 최소 제곱법을 사용하여 상품 변수와 사용자 변수 간의 관계를 모델링하고, 모델을 이용하여 아직 구매하지 않은 상품에 대한 예측 값을 계산합니다. 이렇게 계산된 예측 값(선호도)이 높은 상위 상품 목록을 사용자에게 추천할 수 있습니다.

• Check Point

1. 최소 제곱법은 일반적으로 선형 회귀 모델에 적용되는 방법이기 때문에, 추천 시스템에서는 상품과 사용자의 선호도를 선형적인 관계로 모델링한다는 가정이 필요합니다. 따라서, 추천 시스템에서 최소 제곱법을 사용하기 전에 이 가정이 적절한지 검토해야 합니다.
2. 최소 제곱법은 이상치(outlier)나 데이터 분포의 비선형성 등에 민감할 수 있으므로, 이러한 문제에 대한 처리가 필요할 수 있습니다.

Alternating Least Square

• ALS 목적함수
  
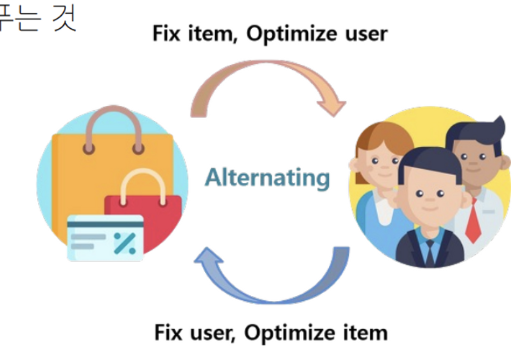
• 동작 방식
  
  ALS의 메인 아이디어는 MF에 사용되는 사용자와 아이템 잠재벡터 이렇게 두 종류의 파라미터를 서로 번갈아가면서 업데이트를 한다는 것이다. 즉, P와 Q 중 하나를 고정해놓고 다른 하나를 업데이트하는 방식이다.

  • 각각을 고정했을 때의 목적식
    $\begin{aligned} & \min _{p_{u}}\left\|r_{u}-Q p_{u}\right\|^{2}+\lambda\left\|p_{u}\right\|^{2} \\ & \min _{q_{i}}\left\|r_{i}-P q_{i}\right\|^{2}+\lambda\left\|q_{i}\right\|^{2} \end{aligned}$

$p_{u} \text { 의 목적함수 } \quad \min _{p_{u}}\left\|r_{u}-Q p_{u}\right\|^{2}+\lambda\left\|p_{u}\right\|^{2}$

1. 목적함수 전개

   $\begin{aligned} L\left(p_{u}\right) & =\left\|r_{u}-Q p_{u}\right\|^{2}+\lambda\left\|p_{u}\right\|^{2} \\ & =\left(r_{u}-Q p_{u}\right)^{T}\left(r_{u}-Q p_{u}\right)+\lambda p_{u}{ }^{T} p_{u} \\ & =r_{u}{ }^{T} r_{u}-r_{u}{ }^{T} Q p_{u}-p_{u}^{T} Q^{T} r_{u}+p_{u}^{T} Q^{T} Q p_{u}+\lambda p_{u}{ }^{T} p_{u} \\ & =r_{u}{ }^{T} r_{u}-2 r_{u}{ }^{T} Q p_{u}+p_{u}^{T} Q^{T} Q p_{u}+\lambda p_{u}{ }^{T} p_{u} \end{aligned}$

2. 목적함수를 파라미터로 미분하기

   $\begin{aligned} \frac{\partial L\left(p_{u}\right)}{\partial p_{u}} & =\frac{\partial}{\partial p_{u}}\left(r_{u}{ }^{T} r_{u}-2 r_{u}{ }^{T} Q p_{u}+p_{u}^{T} Q^{T} Q p_{u}+\lambda p_{u}{ }^{T} p_{u}\right) \\ & =-2 r_{u}{ }^{T} Q+2 p_{u}^{T} Q^{T} Q+2 \lambda p_{u}{ }^{T} \end{aligned}$

3. 목적함수의 미분값을 0으로 설정한 후에 최적 파라미터를 구한다.

$\begin{gathered} -2 r_{u}^{T} Q+2 p_{u}^{T} Q^{T} Q+2 \lambda p_{u}^{T}=0 \\ p_{u}^{T} Q^{T} Q+\lambda p_{u}^{T}=r_{u}^{T} Q \\ p_{u}^{T}\left(Q^{T} Q+\lambda I\right)=r_{u}^{T} Q \\ \left(Q^{T} Q+\lambda I\right)^{T} p_{u}=Q^{T} r_{u} \\ \left(Q^{T} Q+\lambda I\right) p_{u}=Q^{T} r_{u} \\ p_{u}=\left(Q^{T} Q+\lambda I\right)^{-1} Q^{T} r_{u} \end{gathered}$

4. ALS를 사용한 MF의 파라미터 업데이트 수식
   $\begin{aligned} & p_{u}=\left(Q^{T} Q+\lambda I\right)^{-1} Q^{T} r_{u} \\ & q_{i}=\left(P^{T} P+\lambda I\right)^{-1} P^{T} r_{i} \end{aligned}$

• Plus
  numpy.linalg.solve(A,B): Ax=B에서 x를 찾아준다.

• Implicit Feedback을 고려해보자!
  
• 유저 u가 아이템 i를 선호하는 지 여부(Preference)를 Binary로 표현하여 사용한다.
  
• 사용자가 아이템을 얼마나 선호하는지를 나타낸 Confidence 값을 정의한다. 여기서 α는 인터랙션(positive feedback, negative feedback)이 있는 경우 r의 중요도를 조절하는 하이퍼파라미터이다.
  
• 목적함수: r -> f(Preference)로 변환한 후, 얼마나 선호하는 지(Confidence를) 정보를 곱해주었다.
  
• Preference와 Confidence를 고려한 업데이트 수식

• ALS와 SGD
  ALS는 SGD와 다르게 데이터 포인트를 순차적으로 업데이트 하지 않아도 되고 주어진 행렬을 가지고 계산하면 되기 때문에 행렬을 쪼개서 분산처리가 가능하여 학습 속도가 매우 빠르다.

ALS는 또한 Sparse한 데이터에 대해 SGD보다 강건(Robust)한 모습을 보인다. Implicit Feedback의 경우 Explicit Feedback보다 더 Sparse한 경향이 있다. 따라서 Implicit Feedback에는 SGD보다 ALS를 사용하는 것이 유리하다.
Sparse하다: 아이템에 대한 정보가 적고, 사용자와 아이템 간의 연결이 드문 경우를 말합니다

• 다음에 공부할 것
  ALS 기반으로 학습한 모델에 대해서 ANN기법을 사용하여 모델을 서빙한다.
  모든 아이템의 유사도를 구하려면 시간이 많이 소요된다.
  accuracy latency 간의 trade-off를 고려해야 한다.
  annoy , faiss 등의 라이브러리를 활용해서 빠른 서빙을 한다.
  ++ 평가지표

• 참고 자료
  위키피디아 Least Square
  ALS 블로그
  Implicit Feedback 데이터에 적합하도록 MF 기반 모델을 설계하여 성능을 향상시킨 논문