다중회귀분석이란?
종속 변수와 여러 독립 변수들 간의 관계를 모델링하는 통계적 기법으로 독립 변수들이 종속 변수에 미치는 영향력과 방향성을 평가하는 것
1. library
# 시작 전 실행.
library(readr)
library(dplyr)
library(tidyr)
library(stringr)
library(tidyverse)2. 데이터 호출 및 정제
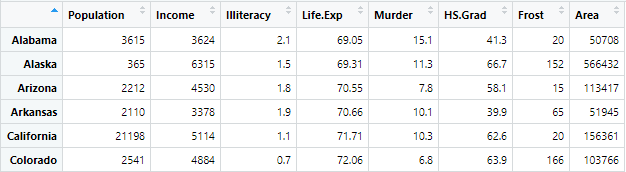
- 사용 데이터: state.x77
- names(): 인구수, 수입, 문맹률, 기대수명, 범죄율, 고졸, 결빙일수, 면적
- as.data.frame(): 데이터 프레임으로 타입 변환
- rename(): 컬럼명 변경
data(state)
stateDF <- state.x77 %>% as.data.frame() %>% rename("Life.Exp"="Life Exp", "HS.Grad"="HS Grad")▼ Console ▼
3. 다중회귀분석 실시
- 목적: 미국 50개 주에 대한 통계데이터(state.x77)에서 Life.Exp(기대수명)변수에 대해 'Population(인구 수), Income(수입), Illiteracy(문맹률), Murder(범죄율), HS.Grad(고졸), Frost(결빙일수), Area(면적)'이 미치는 영향력과 방향성 평가
※ 모델 생성 전 훈련 및 검증, 테스트 데이터로 나눈 후 진행하여야 하지만, 본 과정의 최종 분석 목적은 '전 인구의 55%가 고졸이고 살인비율이 10만명당 8명일 때 Life.Exp(기대수명)의 결과값 예측' 을 하는 것으로 데이터를 나누지 않겠습니다.
1-1) 독립변수: 종속변수 제외 전부
(1) 회귀분석 모델 생성
model1 <- lm(Life.Exp ~ ., data = state.x77) summary(model1)▼ Console of summary ▼
Call:
lm(formula = Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad + Frost + Area, data = stateDF)Residuals:
Min 1Q Median 3Q Max
-1.48895 -0.51232 -0.02747 0.57002 1.49447
Coefficients:
_ Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.094e+01 1.748e+00 40.586 < 2e-16 ***
Population 5.180e-05 2.919e-05 1.775 0.0832 .
Income -2.180e-05 2.444e-04 -0.089 0.9293
Illiteracy 3.382e-02 3.663e-01 0.092 0.9269
Murder -3.011e-01 4.662e-02 -6.459 8.68e-08 ***
HS.Grad 4.893e-02 2.332e-02 2.098 0.0420 *
Frost -5.735e-03 3.143e-03 -1.825 0.0752 .
Area -7.383e-08 1.668e-06 -0.044 0.9649
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.7448 on 42 degrees of freedom
Multiple R-squared: 0.7362, Adjusted R-squared: 0.6922
F-statistic: 16.74 on 7 and 42 DF, p-value: 2.534e-10
(2) 해석
- (Intercept): 회귀 모델의 절편, 종속 변수외 나머지 독립변수 들이 0일 때의 종속 변수의 추정 값
- Coefficients (회귀계수): 독립 변수와 종속 변수 간의 관계를 이해하고 예측하기 위한 정보 제공① Residual Standard Error (잔차 표준 오차)
⒜ 정의
- 예측값과 실제 관측값 사이의 평균 제곱 오차의 제곱근으로 작은 값일 수록 모델의 예측이 관측값과 가까움
⒝ 해석
잔차 표준 오차의 값은 0.7448이므로 모델의 적합도 및 예측 성능이 높다. (※ 0.7448은 백분율이 아님)
② Multiple R-squared (다중 결정 계수) & Adjusted R-squared (수정된 결정 계수)
⒜ 정의
- 다중 결정 계수: 회귀 모델이 종속 변수의 변동을 얼마나 잘 설명하는지를 나타내는 지표로 백분율로 표현
- 수정된 결정 계수: 다중 결정 계수를 독립 변수의 개수와 표본 크기를 고려하여 수정한 값
⒝ 해석
※ 종속 변수의 변동(variability): 종속 변수의 값들이 평균으로부터 얼마나 퍼져 있는지를 나타냄
- 다중 결정 계수: 종속 변수의 변동 중 약 73.62%를 설명할 수 있음을 뜻한다. 높을 수록 설명력이 더 좋다.
- 수정된 결정 계수: 종속 변수의 변동 중 약 69.22%를 설명할 수 있음을 뜻한다.높을 수록 설명력이 더 좋다.
정리하자면, 두 계수는 모델의 설명력을 나타내는 지표이지만 약간 다른 측면을 고려한다.
다중 결정 계수는 독립 변수의 수가 증가하면 같이 증가하는 경향이 있어 모델에 불필요한 변수가 추가된다면 값이 높아지는 경향이 있다.
수정된 결정 계수는 이러한 다중 결정 계수의 문제를 고려하여 데이터의 크기를 고려해 모델의 설명력을 조정한 지표로 모델에 추가된 변수가 실제로 유의미한 개선을 가져왔는지를 고려한다. 따라서 수정된 결정 계수가 다중 결정 계수보다 작을 수 있으며, 더 적절한 변수를 사용하고 있는 모델일수록 그 반대가 된다.
또한, 두 계수 모두 1에 가까울 수록 설명력이 높다고 할 수 있지만, 모델에 독립 변수를 추가하는 것이 설명력에 큰 개선을 가져오지 않는 경우인 과적합을 의미하기도 한다. 즉, 다른 데이터에 대한 일반화 능력이 낮아질 수 있으므로 1에 가까울 때에도 변수의 선택과 모델의 복잡성을 고려해야 한다.
따라서, 모델의 평가와 변수 선택에는 두 가지 계수를 함께 고려해야 한다.
③ 검정 통계량
⒜ 정의
- F-statistic: 회귀 모델 전체의 유의성을 평가하는 지표로 값이 클 수록 모델이 통계적으로 유의미한 관계를 가짐
- t-value: 개별 독립 변수의 효과를 평가하는 지표로 독립 변수가 종속 변수에 미치는 영향의 크기와 방향성을 나타냄, 값이 클수록 효과가 통계적으로 유의미 하다는 의미
- p-value: 가설 검정을 통해 얻어진 결과로 참일 확률로 값이 작을 수록 해당 가설이 통계적으로 유의미하다고 판단
⒝ 해석
※ Degrees of Freedom (자유도): 통계 분석에서 모집단의 특정한 특성을 추정하거나 검정하기 위해 사용되는 독립적인 정보의 수로 회귀 분석에서 자유도는 모델의 적합도와 가설 검정에 관련된다.
F-statistic 또는 t-value 의 값과 자유도에 기반하여 p-value를 계산할 수 있다. 이는 F-statistic 값과 p-value를 통해 모델 전체의 유의성을 평가할 수 있으며 각 독립 변수의 t-value와 p-value를 통해 개별 독립 변수의 유의성을 평가할 수 있다는 것이다.
여기서 F-statistic 의 값은 16.74 로 유의수준(0.05)보다 크고 p-value 값은 2.534e-10로 유의수준보다 작은 것을 보았을 때, 적어도 하나의 독립변수가 종속변수와 관련이 있으며 이러한 검정통계량의 유의미 하다는 것을 알 수 있다.
같은 기준으로 t-value와 p-value를 해석한다. Income(수입) & Illiteracy(문맹률) & Area(면적) 변수의 t-value의 절대값이 작고 p-value의 값이 유의수준보다 큰 것을 알 수 있다. 이는 이 세가지 변수가 종속 변수와 유의미한 관련이 없다는 것을 나타낸다.
1-2) Variable Selection (변수 선택 기법)
- 정의: 변수 선택은 모델에 포함되는 독립 변수의 집합을 최적화하여 모델의 예측 성능과 해석력을 향상시키는 것
- 사용기법: 본 과정에서는 모든 변수를 포함한 전체 모델에서 유의하지 않은 변수를 제거하여 성능을 향상시키는 것을 목표로 하므로 이에 가장 알맞는 후진 제거법(Backward Elimination)을 사용
# step(): 기존 회귀모형에서 유의하지 않은 변수를 제거.
model2 <- step(model1, direction = "backward")
summary(model2)▼ Console▼
- 과정 *두번째만, 나머지 과정은 생략
Start: AIC=-22.18
Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad + Frost + AreaDf Sum of Sq RSS AIC
- Area 1 0.0011 23.298 -24.182
- Income 1 0.0044 23.302 -24.175
- Illiteracy 1 0.0047 23.302 -24.174
(none) 23.297 -22.185
- Population 1 1.7472 25.044 -20.569
- Frost 1 1.8466 25.144 -20.371
- HS.Grad 1 2.4413 25.738 -19.202
- Murder 1 23.1411 46.438 10.305
Step: AIC=-24.18
Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad + FrostDf Sum of Sq RSS AIC
- Illiteracy 1 0.0038 23.302 -26.174
- Income 1 0.0059 23.304 -26.170
(none) 23.298 -24.182
- Population 1 1.7599 25.058 -22.541
- Frost 1 2.0488 25.347 -21.968
- HS.Grad 1 2.9804 26.279 -20.163
- Murder 1 26.2721 49.570 11.569
해석
모든 변수가 포함된 AIC는 -22.18이다. 각 변수를 제거하여 제곱합 및 잔차 제곱합, AIC의 값을 보았을 때 Area 변수를 제거 한 것이 가장 유의미한 것을 알 수 있다. 따라서, 다음 step 에서는 Area를 제외한 모델로 후진 제거법을 진행한다.
Area를 제거한 것과 같은 과정이 반복 되다가, 현재 단계의 모델이 최적의 성능이 된다면(어떠한 변수를 제거한 모델이 현재 모델 보다 낮은 성능)이라면 후진 제거법을 멈추게 되고 최종 모델이 된다.
※ 참고 ※
- Sum of Squares (SS, 제곱합)
└ 변수 선택 기법에서는 변수의 추가 또는 제거로 인해 제곱합이 어떻게 변화하는지를 평가하여 모델의 성능을 판단
└ 회귀 분석에서 제곱합은 모델의 예측값과 실제 관측값 간의 차이를 제곱하여 합한 값- Residual Sum of Squares (RSS, 잔차 제곱합)
└ 변수 선택 기법에서는 변수를 추가하거나 제거함으로써 잔차 제곱합이 최소화되는 모델을 선택
└ 회귀 모델에서 예측값과 실제 관측값 간의 차이의 제곱의 합- Akaike Information Criterion (AIC, 아카이케 정보 기준)
└ 변수 선택 기법에서는 AIC가 가장 작은 모델을 선택 (작을수록 데이터를 잘 설명하는 모델)
└ 모델의 적합도와 복잡성을 고려하는 선택 기준으로 모델의 잔차 제곱합과 변수의 수를 고려하여 계산=> 3가지 모두 값이 적을수록 좋다.
- 기술 통계
Call:
lm(formula = Life.Exp ~ Population + Murder + HS.Grad + Frost, data = stateDF)Residuals:
Min 1Q Median 3Q Max
-1.47095 -0.53464 -0.03701 0.57621 1.50683
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.103e+01 9.529e-01 74.542 < 2e-16 ***
Population 5.014e-05 2.512e-05 1.996 0.05201 .
Murder -3.001e-01 3.661e-02 -8.199 1.77e-10 ***
HS.Grad 4.658e-02 1.483e-02 3.142 0.00297 **
Frost -5.943e-03 2.421e-03 -2.455 0.01802 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.7197 on 45 degrees of freedom
Multiple R-squared: 0.736, Adjusted R-squared: 0.7126
F-statistic: 31.37 on 4 and 45 DF, p-value: 1.696e-12
해석: 전체적으로 기존 모델보다 성능이 조금 향상 되었지만, 변수 제거로 인한 통계적 유의미성은 미미하다.
기존 모델에서 후진 제거법을 통해 유의미하지 않은 변수들을 제거했다. 그 결과 잔차 표준 오차는 0.7448 → 0.7197, p-value는 2.534e-10 → 1.696e-12로 감소 되었으며, 수정된 결정 계수는 69.22% → 71.26%, F-statistic은 16.74 → 31.37로 증가 되었다. 또한, 각 독립 변수의 t-value의 절대값은 증가하였으며 p-value 역시 유의미한 결과로 확인된다.
하지만 두 개의 모델을 비교한 아래 결과를 살펴보면, 변수 선택 기법에 의한 변수 제거는 항상 통계적으로 유의미한 결과를 도출하지 않음을 알 수 있다. 즉, 변수 제거로 인해 모델의 설명력이 크게 변하지 않았거나, 제거된 변수가 종속 변수와 상관성이 적어서 유의미한 영향을 주지 못했을 가능성이 있다. 그러므로 경우에 따라 변수의 중요성과 데이터의 특성을 고려하여 모델을 평가할 필요가 있다.
anova(model2, model1)▼ Console▼
Analysis of Variance Table
Model 1: Life.Exp ~ Population + Murder + HS.Grad + Frost
Model 2: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad + Frost + AreaRes.Df RSS Df Sum of Sq F Pr(>F)
1 45 23.308
2 42 23.297 3 0.010905 0.0066 0.9993
※ 참고 ※
- Res.Df (잔차 자유도): 모델에서 사용되지 않은 독립 변수의 개수, 값이 커야 모델이 더 좋은 적합도 가짐- RSS (잔차 제곱합): 예측 값과 실제 값 사이의 차이를 제곱하여 합한 값, 값이 작을수록 모델의 적합도가 더 좋음
- Df (자유도)
└ 모델에서 사용된 독립 변수의 개수 나타내는 것으로 모델이 데이터를 얼마나 유연하게 표현할 수 있는지를 나타내는 척도
└ 모델의 복잡성을 나타내기 때문에, 과적합을 방지하기 위해 적절한 수준에서 관리 필요
└ 변수의 자유도가 적절하면 모델이 더 좋은 일반화 성능을 가짐- Sum of Sq (제곱합): 모델이 얼마나 많은 변동을 설명하는지를 나타내는 척도로 값이 클수록 좋지만, 다른 요소와 함께 고려해야 함
- F (F-statistic): 모델의 설명된 변동과 설명되지 않은 잔차 변동 사이의 비율을 계산한 값으로 클수록 좋음
- Pr(>F) (p-value): F-statistic 대한 유의확률로 유의수준보다 작으면 통계적 유의성 높아짐
따라서, 이 다음 과정에서는 model2에서 가장 유의미한 변수 두 가지 Murder(범죄율)과 HS.Grad(고졸)을 독립변수로 하는 모델을 생성하여 기존 모델(model1, model2)과 비교한다.
2) HS.Grad 및 Murder 변수
Life.Exp 를 종속변수로, HS.Grad와 Murder 변수를 독립변수(예측 변수)로 설정하여 다중 회귀분석 실시한다.
(1) 회귀분석 모델 생성
model3 <- lm(Life.Exp ~ HS.Grad + Murder, data = stateDF)
summary(model3)▼ Console of summary ▼
Call:
lm(formula = Life.Exp ~ HS.Grad + Murder, data = stateDF)Residuals:
Min 1Q Median 3Q Max
-1.66758 -0.41801 0.05602 0.55913 2.05625Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 70.29708 1.01567 69.213 < 2e-16 ***
HS.Grad 0.04389 0.01613 2.721 0.00909 **
Murder -0.23709 0.03529 -6.719 2.18e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.7959 on 47 degrees of freedom
Multiple R-squared: 0.6628, Adjusted R-squared: 0.6485
F-statistic: 46.2 on 2 and 47 DF, p-value: 8.016e-12
> 해석
: 가장 유의미했던 독립변수들로만 구성하여 모델을 생성했지만, 오히려 model2보다 성능이 낮은 것을 알 수 있다. 따라서 원인을 분석하기 위해 생성된 모델 3가지를 비교한다.
(2) 모델 비교
model3(독립변수: HS.Grad, Murder) 및 model2(독립변수: Population, Murder, HS.Grad, Frost), model1(독립변수: 종속변수 제외 전부) 를 비교를 한다.
anova(model3, model2, model1) ※ anova 함수를 사용할 때 주의할 점: 처음 입력한 모델과 그 후에 입력한 모델들을 차례로 비교하므로, 비교할 모델이 3개 이상이라면 모델 입력 순서에 주의해야 한다.
▼ Console ▼
Analysis of Variance Table
Model 1: Life.Exp ~ HS.Grad + Murder # model3
Model 2: Life.Exp ~ Population + Murder + HS.Grad + Frost # model2
Model 3: Life.Exp ~ Population + Income + Illiteracy + Murder + HS.Grad + Frost + Area # model1Res.Df RSS Df Sum of Sq F Pr(>F)
1 47 29.770
2 45 23.308 2 6.4623 5.8251 0.005851 **
3 42 23.297 3 0.0109 0.0066 0.999259
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
> 해석
- model3 vs model2 (Console 기준: Model1 vs Model2)
: F-statistic 이 유의수준 보다 크고 p-value 는 유의수준 보다 작으므로 두 모델 사이에 유의미한 차이가 있다.- model2 vs model1 (Console 기준: Model2 vs Model3)
: F-statistic 이 유의수준 보다 작고 p-value 는 유의수준 보다 크므로 두 모델 사이에 유의미한 차이가 없다.
>> model2가 다른 두 모델 model1과 model3보다 Life.Exp(기대수명)을 설명하는 데 더 좋은 모델이라고 볼 수 있다. 하지만 이 결과만으로 판단하여 결과를 도출하기 보다는 분석 목적 등 다양한 요소를 함께 고려해야 하는 점을 주의해야 한다.
3) 모델에 대한 종합 해석
첫 모델인 'model1' 에서는 종속변수를 제외한 모든 변수를 독립변수로 설정하여 다중회귀분석을 실시했다. 기술 통계량을 출력했을 때, 전체적으로는 통계적으로 유의미하지만 단일 독립변수의 값을 보았을 때 일부 유의미하지 않은 것이 확인된다.
따라서, 해당 변수들을 제거한 두번째 모델 'model2' 를 생성한 후 마찬가지로 기술 통계량을 출력했다. 전체적으로도 단일 독립변수를 보았을 때도 통계적으로 유의미하다고 판단했다. 하지만, 'model1' 과 비교해 보았을 때 사실상 성능에 큰 차이가 있지 않다는 것이 확인 되었다.
그래서 'model2' 의 독립변수 중 가장 유의미한 두 개의 변수를 선택해 새로운 모델 'model3' 를 생성한 후 기술 통계량을 출력했다. 예상했던 것과는 달리 'model2' 보다 좋지 않은 결과를 보였다.
이 세 개의 모델을 보다 쉽게 비교하기 위해 anova 함수를 사용하여 비교 결과를 출력하였다. 각 모델의 기술 통계량을 분석하여 비교한 것과 같은 결과가 나타났다.
이를 통해 알 수 있는 사실은 유의미한 독립변수들로만 구성한다고 해서 좋은 모델이라고 할 수 없고, 유의미하지 않다고 판단된 변수들을 제거하면 무조건 훨씬 좋은 모델이 된다는 것도 아니라는 것이다. 그렇기 때문에 모델을 만들 때에는 수치를 세밀하게 판단하고 다양한 방법을 사용하여 신중한 분석이 필요하다.
4. 예측
- 조건: 전 인구의 55%가 고졸이고 살인비율이 10만명당 8명일 때 Life.Exp(기대수명)의 결과값 예측
※ 모델의 기술통계량에서 알 수 있는Intercept(절편) & Estimate Std.(추정치의 표준오차) 를 사용할 예정이므로 각 모델의 기술통계량 참고 부탁드립니다.
1) 사용자 정의 함수
(1) 절편 + (추정치의 표준오차 * 살인비율 10만명당 8명) + (추정치의 표준오차 * 55%가 고졸)
# 공식사용 # model3 pre1_Model3 <- function(mur, hs) { lifeExp <- 70.29708 + (-0.23709*mur) + (0.04389*hs) return(lifeExp) } # model2 pre1_Model2 <- function(df, mur, hs) { lifeExp <- 0 for(i in 1:nrow(df)) { lifeExp <- lifeExp + ( 71.03 + (5.014e-05 * df$Population[i]) - (0.3001 * mur) + (0.04658 * hs) - (0.005943 * df$Frost[i]) ) } return(lifeExp/nrow(df)) }
(2) predict ( model, newdata = df )
# predct 함수 사용 # model 3 pre2_Model3 <- function(mur, hs) { return(predict(model3, newdata = data.frame(Murder = mur, HS.Grad = hs))) } # model2 pre2_Model2 <- function(df, mur, hs) { lifeExp <- 0 for(i in 1:nrow(df)){ lifeExp <- lifeExp + predict(model3, newdata = data.frame(Population = df$Population[i], Murder = mur, HS.Grad = hs, Frost = df$Frost[i])) } return(lifeExp/nrow(df)) }
2) 실행
# 기대 수명치 평균값 (실제 관측값)
mean(stateDF$Life.Exp) # =console=> 70.8786
# 공식 사용
pre1_Model3(8, 55); pre1_Model3(8, 0.55); pre1_Model3(0.8, 55); pre1_Model3(0.8, 0.55)
pre1_Model2(stateDF, 8, 55); pre1_Model2(stateDF, 8, 0.55); pre1_Model2(stateDF, 0.8, 55); pre1_Model2(stateDF, 0.8, 0.55)
# 함수 사용
pre2_Model3(8, 55); pre1_Model3(8, 0.55); pre1_Model3(0.8, 55); pre1_Model3(0.8, 0.55)
pre2_Model2(stateDF, 8, 55); pre2_Model2(stateDF, 8, 0.55); pre2_Model2(stateDF, 0.8, 55); pre2_Model2(stateDF, 0.8, 0.55)(1) 비교
▼ 공식 사용 ▼ ▼ 함수 사용 ▼
| model3 | model2 | model3 | model2 | ||
|---|---|---|---|---|---|
1 (8, 55) | 70.81431 | 70.78321 | 70.81416 | 70.81416 | |
| ────── | ────── | ────── | ────── | ────── | |
| 2 (8, 0.55) | 68.4245 | 68.24693 | 68.4245 | 68.4245 | |
| ────── | ────── | ────── | ────── | ────── | |
| 3 (0.8, 55) | 72.52136 | 72.94393 | 72.52136 | 72.52121 | |
| ────── | ────── | ────── | ────── | ────── | |
| 4 (0.8, 0.55) | 70.13155 | 70.40765 | 70.13155 | 70.13155 |
(2) 해석
실제 관측값의 평균이 70.8786 인 점을 고려하여 해석한다.
첫번째로, 변수 영력 조절에 대한 각 결과를 비교했을 때, 공식 또는 함수 사용 여부에 관계 없이 영향력을 크게 했을 때 예측값이 실제 관측값에 가장 가까웠다. 이는 55%의 고졸과 10만명단 8명의 살인비율이라는 조건이 정확하게 명시되어 있으므로 정확하게 반영하기 위해 변수의 영향력을 크게 조절했기 때문이다. 만약, 조건이 명시되어 있지 않은 경우라면, 일반적인 비율을 사용하는 것도 좋다.
두번째로, 예측 방법의 차이에 대한 결과와 서로 다른 모델을 사용했을 때의 결과 를 비교한다. 두 가지 경우 모두 큰 차이가 나지 않으므로, 사용자가 편한 방법을 택하면 된다.
따라서, 코드가 가장 단순하면서 실제 관측값에 가까운 1번 행 > model3 의 값을 최종 예측 값으로 선택하겠다. 이처럼 예측하는 과정을 통해 제일 성능이 높다 생각했던 model2보다 분석목적에 잘 맞는 model3을 사용했을 때 보다 쉽게 진행했음을 알 수 있으므로 다양한 모델을 사용하여 각 예측값과 실제 관측값을 비교분석 후 결과를 도출해야 한다.
5. 시각화
1) 생성
- expend.grid(): HS.Grad(고졸) 및 Murder(범죄)의 범위를 seq 함수를 사용해 조합을 생성
- predict(): model3로 생성한 조합의 예측값 산출
library(rgl)
plotdat <- expand.grid(HS.Grad=seq(min(stateDF$HS.Grad),max(stateDF$HS.Grad), by=2)
,Murder=seq(min(stateDF$Murder),max(stateDF$Murder), by=1))
plotdat$pred1 <- predict(model3, newdata=plotdat)
with(stateDF, plot3d(HS.Grad, Murder, Life.Exp, col="blue", size=1, type="s"))
with(plotdat, surface3d(unique(HS.Grad), unique(Murder), pred1, alpha=0.5,front="line", back="line"))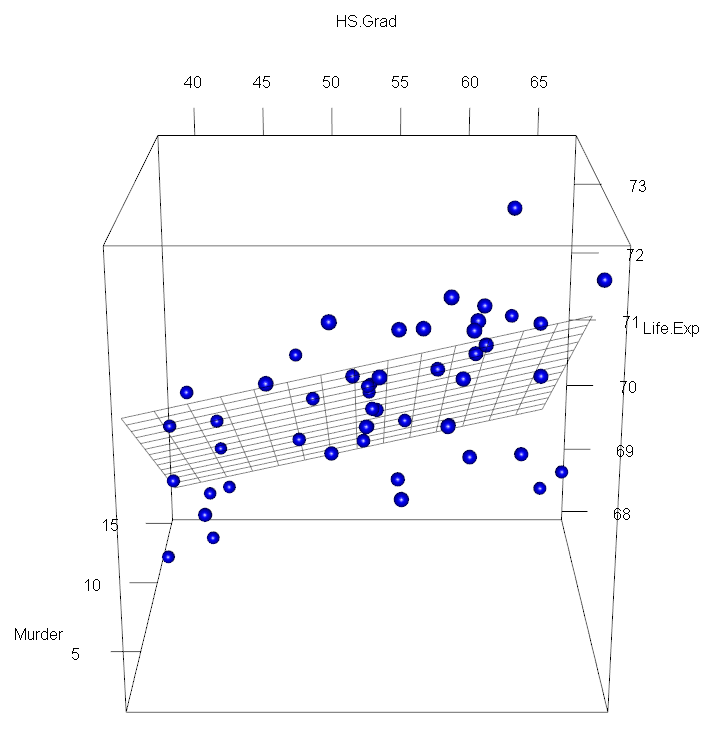
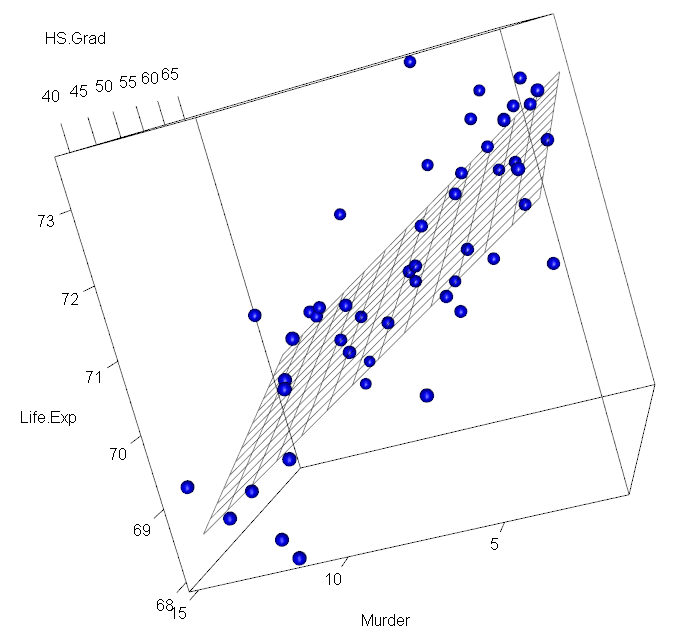
2) 해석
- 양의 관계: 'HS.Grad' (고졸)이 높을수록 'Life.Exp' (기대 수명)이 증가하는 경향을 보인다.
- 음의 관계: 'Murder' (범죄율)이 낮을수록 'Life.Exp' (기대 수명)이 증가하는 경향을 보인다.
기술 통계량의 수치를 분석하는 것보다 그래프를 통해 HS.Grad(고졸), Murder(범죄율)이 Life.Exp(기대수명)에 어떠한 영향을 미치는지를 더 쉽게 파악할 수 있다. 비록 기대 수명에 영향을 미치는 다른 요인을 고려해야 한다는 점을 미루어 보았을 때, 이 두 가지의 영향으로 인한 기대 수명 예측값은 완전한 값이 아니므로 주의해야 한다.
