로지스틱 회귀분석이란?
종속 변수가 이항적인 경우(두 개의 범주를 가지는 경우)에 사용되는 통계적 분석 방법으로 종속 변수와 독립 변수간의 관계를 모델링하고 독립 변수의 값에 따라 종속 변수가 속하는 범주를 예측하는 데 사용됩니다.
분류 문제에 널리 활용되며 예측 모델의 해석이 상대적으로 용이하고 계산적으로 효율적입니다.
1. 데이터 호출
- 사용 데이터: 내장 데이터 mtcars
- 분석 목적: mpg(연비)와 am(변속기종류)가 vs(엔진)에 미치는 영향 확인 및 평가
# 데이터셋 로드
data(mtcars)
help(mtcars)▼ Console of help(mtcars) ▼
Format
A data frame with 32 observations on 11 (numeric) variables. # 32개의 관측치와 11개의 변수로 구성
[, 1] mpg Miles/(US) gallon # 연비
[, 2] cyl Number of cylinders
[, 3] disp Displacement (cu.in.)
[, 4] hp Gross horsepower
[, 5] drat Rear axle ratio
[, 6] wt Weight (1000 lbs)
[, 7] qsec 1/4 mile time
[, 8] vs Engine (0 = V-shaped, 1 = straight) # 0: V-Shaped 엔진, 1: straight 엔진
[, 9] am Transmission (0 = automatic, 1 = manual) # 0: 오토, 1: 스틱
[,10] gear Number of forward gears
[,11] carb Number of carburetors
2. 로지스틱 회귀분석
1) 데이터 분리
모델 생성 전 훈련 및 검증, 테스트용으로 데이터를 분리해 주어야 합니다. 일반적으로 훈련 및 테스트 데이터를 7:3 or 8:2로 분리한 후 훈련 데이터를 훈련 및 검증 데이터로 나눕니다(7:3 or 8:2). 하지만 앞서 살펴본 바와 같이 사용할 데이터의 관측치는 32개로 굉장히 적은 양이고 분석 목적을 생각했을 때 2개의 독립변수만 사용할 예정이므로 검증 데이터 없이 훈련 및 테스트 데이터를 8:2로 나누어 줍니다.
# 데이터 분할
trIdx <- sample(1:nrow(mtcars), 0.8 * nrow(mtcars))
mtcTr <- mtcars[trIdx, ] # 25
mtcTe <- mtcars[-trIdx, ] # 72) 모델 생성
- glm(): R에서 일반화 선형 모델을 생성하기 위해 사용되는 함수로 선형 회귀 뿐만 아니라 옵션을 조정하여 로지스틱 회귀 등 다양한 종류의 선형 모델을 만듦
# 로지스틱 회귀분석을 하기 위해 family 옵션을 binomial로 설정
glmModel <- glm(vs ~ mpg + am, data = mtcTr, family = binomial)
# 결과 요약
summary(glmModel)▼ Console of summary(mtcTr) ▼
Call:
glm(formula = vs ~ mpg + am, family = binomial, data = mtcars)Deviance Residuals:
Min 1Q Median 3Q Max
-2.0585 -0.5189 -0.2513 0.3307 1.6887Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -12.5235 5.1727 -2.421 0.0155 *
mpg 0.6830 0.2927 2.333 0.0196 *
am -3.2436 1.8636 -1.740 0.0818 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1(Dispersion parameter for binomial family taken to be 1)
Null deviance: 33.651 on 24 degrees of freedom
Residual deviance: 18.333 on 22 degrees of freedom
AIC: 24.333Number of Fisher Scoring iterations: 6
※ 참고 ※
로지스틱 회귀분석에서의 Estimate는 로즈 오그 라는 것을 나타냅니다. 이는 종속 변수의 변화를 설명하기 위한 것으로, 해석하기 위해서는 지수함수인 오즈비를 계산해주어야 합니다. 오즈비는 독립변수의 값이 1단위 증가할 때의 확률를 의미합니다.위 기술 통계랑을 예로 들자면, am(변속기종류)의 로즈 오그는 -3.2436으로 am이 1단위가 증가할 때마다 로즈 오그는 3.2436만큼 감소한다는 뜻입니다. 이를 지수함수로 변환하여 해석하면, am이 1단위 증가할 때 vs(엔진)이 0이 될 확률이 1이 될 확률 보다 약 0.038배 낮다고 할 수 있습니다. 즉, am이 1일 때 vs가 1일 확률이 높다는 것입니다.
* 로그 오즈(Log Odds): 어떤 사건이 발생할 확률과 발생하지 않을 확률의 비율을 로그로 취한 값
* 로그 오즈비(Log Odds Ratio): 로그 오즈의 차이를 나타내는 개념, 지수함수 변환 필요(exp 함수사용)
2) 기술통계량 해석
mpg(연비) 단위가 증가하게 되면 vs(엔진)이 0이 될 확률이 증가하고, am(변속기종류) 단위가 증가하게 되면 vs(엔진)이 0이 될 확률이 감소합니다.
또한, Null deviance(귀무편차)의 값보다 Residual deviance(잔차편차)값이 상대적으로 낮고 알고리즘 반복회수가 6으로 모델이 빠른 속도로 최적화 되었으며 절편에서의 p-value가 유의수준보다 낮은 것 등을 살펴보았을 때 대체적으로 유의미한 모델이라고 판단 됩니다.
비록 각 독립변수에 대한 p-value가 유의수준 보다 높지만, 분석 목적에 필요한 독립변수이므로 일단 제외하지 않고 진행 합니다.
※ 참고 ※
- Null deviance(귀무편차): 모든 독립변수를 사용하지 않고 종속변수의 평균값만 사용하여 예측하는 모델로 종속 변수의 변동성을 나타내며 낮을 수록 좋음
- Residual deviance(잔차편차): 모델이 예측한 값과 실제 관측값 간의 차이의 편차를 나타내는 것으로 모델이 데이터에 적합한 정도를 뜻하며 낮을 수록 좋음
=> 잔차편차의 값이 귀무편차에 비해 상대적으로 작다면 모델의 성능이 높다는 의미로 로지스틱 회귀분석에서 모델의 적합도를 평가하기 위해 사용되는 통계량임- Number of Fisher Scoring iterations: Fisher Scoring 알고리즘이 반복적인 과정을 통해 모델의 매개변수를 조정하여 모델의 우도를 최대화 하는 값을 찾는 과정의 반복 횟수를 나타냄
└ 일반적으로 반복 횟수가 많다면 모델은 더욱 정교하게 적합되지만 수렴하는 데 시간이 오래 걸릴 수 있는데 이는 모델 적합의 속도와 정확도 사이의 절충점을 나타내는 것
└ Fisher Scoring: 로지스틱 회귀모델의 최적화 알고리즘 중 하나로 likelihood(최대우도) 추정을 수행
└ likelihood 추정: 모델의 매개변수(회귀계수)를 데이터에 가장 잘 적합한 값을 찾는 과정- Dispersion parameter for binomial family taken to be 1: 로지스틱 회귀분석에서 사용된 확률 분포인 'binomial'에서의 분산 파라미터(dispersion parameter)를 1로 설정했다는 것을 의미하는 것으로 이는 로지스틱 회귀분석에서는 일반적임
3. 예측 및 평가
1) 예측하기
모델 생성 전 분리 해주었던 테스트 데이터를 사용하여 예측합니다. 종속변수가 0 아니면 1 이라는 이항적인 성격이므로, 0.5를 기준으로 작으면 0, 아니면 1 로 예측 값을 설정해줍니다.
# 모델을 적용하여 예측 수행
moPred <- ifelse(predict(glmModel, newdata = mtcTe, type = "response") >= 0.5, 1, 0)
# 예측 결과 확인
moRes <- data.frame(mpg = mtcTe$mpg, am = mtcTe$am, predVs = moPred, trueVs = mtcTe$vs)▼ Console ▼
| predVs | trueVs | |
|---|---|---|
Hornet 4 Drive | 1 | 1 |
| ────────── | ─────── | ─────── |
| Merc 230 | 1 | 1 |
| ────────── | ─────── | ─────── |
| Cadillac Fleetwood | 0 | 0 |
| ────────── | ─────── | ─────── |
| Lincoln Continental | 0 | 0 |
| ────────── | ─────── | ─────── |
| Fiat 128 | 1 | 1 |
| ────────── | ─────── | ─────── |
| Honda Civic | 1 | 1 |
| ────────── | ─────── | ─────── |
| Pontiac Firebird | 1 | 0 |
> 7개의 테스트 데이터 중 1개의 예측이 틀렸습니다.
2) 변수 간 관계 확인
기술 통계 분석 시 Estimate의 값을 통해 예측 했던 변수 간의 관계를 시각화 하여 한번에 파악할 수 있게 시각화 하겠습니다.
# mpg와 vs의 관계 & 예측값과 관측값
ggplot(moRes, aes(x = mpg)) +
geom_point(aes(y = predVs, color = "Predicted"), size = 3) +
geom_point(aes(y = trueVs, color = "Observed"), size = 3) +
geom_line(aes(y = predVs, color = "Predicted"), size = 1) +
geom_line(aes(y = trueVs, color = "Observed"), size = 1, linetype = "dashed") +
labs(x = "mpg", y = "vs", color = "Value") +
scale_color_manual(values = c("Predicted" = "blue", "Observed" = "red")) +
theme_minimal() +
coord_flip()
# am과 vs의 관계 & 예측값과 관측값 는 mpg의 것과 동일하므로 생략합니다.(1) 독립변수 mpg & 종속변수 vs
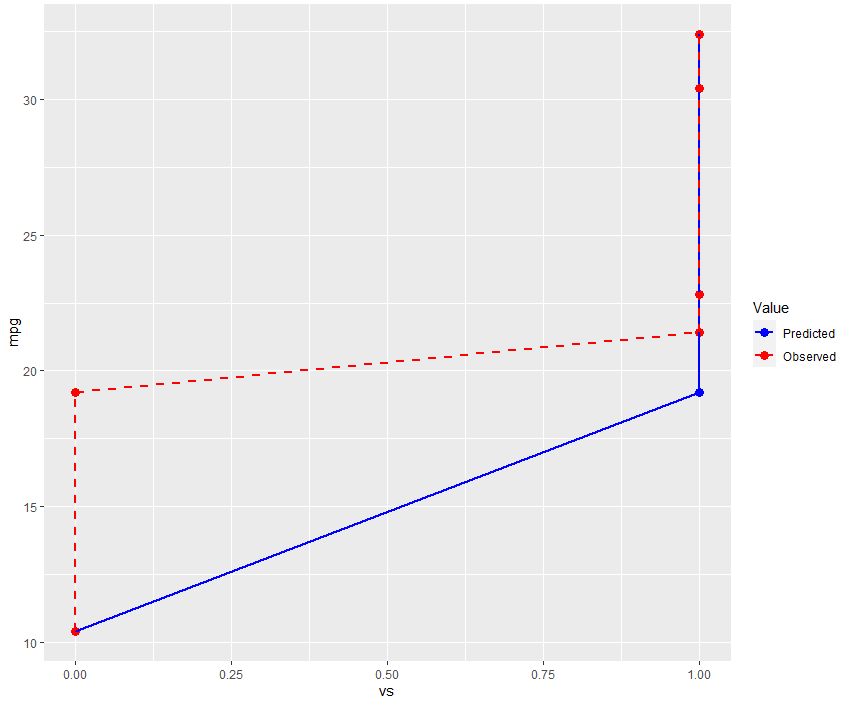
예측값된 값들이 표현된 파란색과 관측값들이 표현된 빨간색이 유사한 경향을 보이고 있습니다. 이는 모델이 mpg 값을 잘 활용하여 vs 값을 예측하고 있다는 뜻입니다. 또한 mpg가 증가할 수록 vs가 0에서 1로 바뀌는 것을 알 수 있습니다.
두 변수의 관계를 통해 알 수 있는 사실은 연비(mpg)가 높으면 straight Engine(vs 값 1)일 것이고, 연비가 낮으면 V-shaped Engine(vs 값 0)이라는 것 입니다.
(2) 독립변수 am & 종속변수 vs
① 테스트 데이터
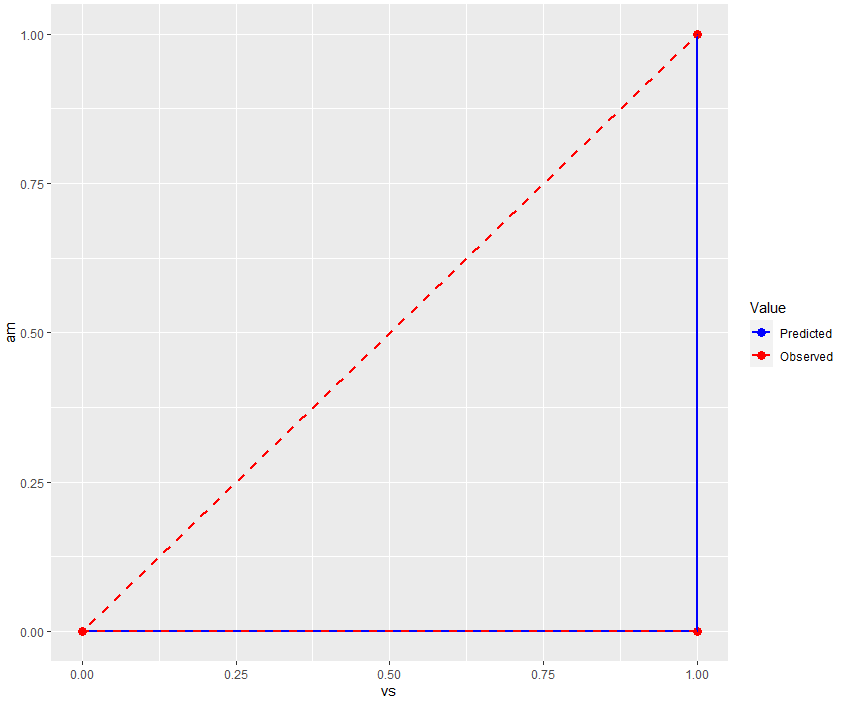
예측값된 값들이 표현된 파란색과 관측값들이 표현된 빨간색이 유사한 경향을 보이고 있습니다. 이는 모델이 am 값을 잘 활용하여 vs 값을 예측하고 있다는 뜻입니다. 하지만 am의 값이 0일 때 vs 값이 0일 때도 있는 것을 보았을 때, am이 vs한테 미치는 영향이 미미한 것으로 보입니다.
추가로 전체 데이터를 대상으로 하여 동일한 과정을 통해 그래프를 만들겠습니다.
② 전체 데이터
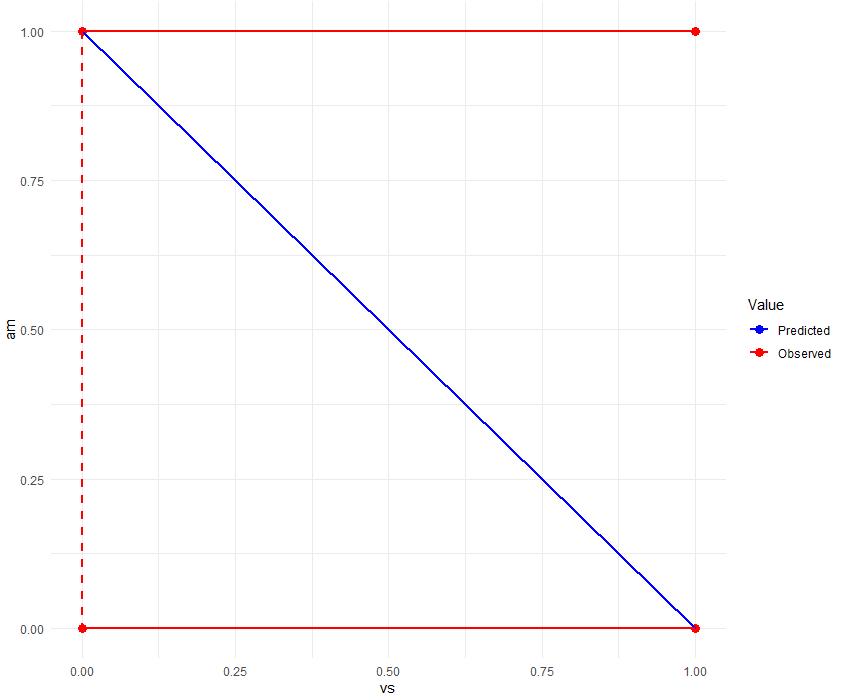
얼핏보면 ①의 결과와 반대인 것처럼 보이지만 비슷한 경향을 띄고 있습니다. 자세히 살펴보면 관측 값(빨간색)들의 경우 am이 0일 때 vs가 0과 1 모두 존재하고(am 1일 때도 마찬가지) 예측 값(파란색)들의 경우 음의 선형 관계를 보여주는 데 이는 모델이 am과 vs의 관계를 보는 방식을 알려줍니다.
예측 값과 관측 값은 서로 일치하는 경향을 보이지만, vs에게 am이 미치는 영향은 작거나 없다는 것을 알 수 있습니다.
3) 모델 평가
이진 분류 모델의 성능을 평가하고 비교하는 데 주로 사용하는 ROC 그래프를 사용하여 시각화 합니다. ROC 그래프는 모델의 성능을 종합적으로 평가하는 데 사용되며 AUC(Area Under the Curve)를 계산하여 수치로 평가할 수 있습니다.
AUC는 ROC 곡선 아래의 면적을 계산한 값으로 0부터 1까지의 범위를 가지며, 0.5보다 크고 1에 가까워질수록 모델의 성능이 좋다고 판단할 수 있습니다.
└ AUC < 0.5: 무작위 예측보다 성능이 나쁨
└ AUC 0.5에 가까움: 모델의 성능이 무작위 수준에 가까움
└ AUC 1에 가까움: 모델의 성능이 좋음
※ 참고 ※
양성(예측) 음성(예측)
양성(실제)
TP(True Positive)
FN(False Negative)────── ───────── ────────── 음성(실제) FP(False Positive) TN(True Negative) > FP은 1종 오류(TypeⅠError), FN은 2종 오류(TypeⅡError) 라고도 불림
- ROC 곡선은 모델의 예측 결과를 다양한 값으로 조정하면서 진짜 양성 비율(TPR)과 가짜 양성 비율(FPR) 사이의 관계를 표현
⇒ TPR(True Positive Rate): 실제 양성 중 정확하게 예측한 비율, 예측 양성 → 실제 양성 (called 민감도 or 재현율)
⇒ 민감도(Sensitivity): 예측 양성 → 실제 양성 비율
⇒ FPR(False Positive Rate): 실제 음성 중 잘못 예측한 비율 (가짜 양성 비율), 예측 양성 → 실제 음성
⇒ 특이도(Specificity): 예측 음성 → 실제 음성 비율, 1-특이도=FPR
library(pROC)
# ROC 그래프를 위해 mtcRes 타입 변환
mtcRoc <- roc(mtcRes$observed, mtcRes$predictions)
# ROC 그래프
plot(mtcRoc, main = "ROC Curve", xlab = "FPR", ylab = "TPR", xlim = c(1, 0), ylim = c(0, 1))
# 대각선 기준선 추가
abline(a = 0, b = 1, lty = 2)
# AUC 계산
legend("bottomright", paste("AUC =", round(auc(mtcRoc), 2)))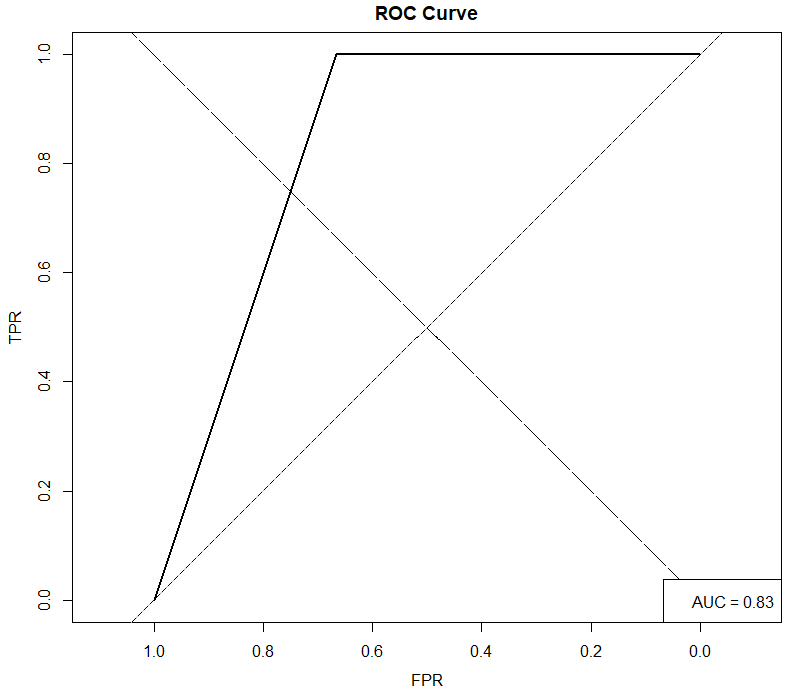
좌측상단으로 갈수록 성능이 우수한 모델임을 나타내는데, 해당 그래프를 보았을 때 ROC 곡선이 좌측 상단에 위치해 있으며, AUC 또한 0.83으로 적은 데이터 대비 높은 성능을 보여주고 있습니다.
4. 해석
모델의 기술 통계량 분석했을 때 각 독립변수의 p-value 값이 유의수준보다 높아 높은 성능을 기대하기 어려웠지만 해당 독립변수들은 분석 목적에 꼭 필요한 것이었고, 모델 자체(전체)에 대한 p-value 값은 낮은 것 등 다른 요인을 고려하여 그대로 진행하였습니다.
변수 간 관계 확인 및 모델 평가를 통해 얻은 사실은 모델 자체의 성능은 좋은 편이나, 독립변수 am(변속기 종류)는 종속변수 vs(엔진)에 유의미한 영향이 미친다고 할 수 없다는 것입니다. 이는 예측값이 mpg(연비)의 영향으로 나왔다고 할 수도 있습니다.
하지만 본 과정에서 사용한 데이터의 크기 자체가 굉장히 작았기 때문에 이 결과를 일반화하기에는 무리가 있습니다. 따라서, 데이터의 양이 작을 때에는 결과 보단 과정에 집중하는 것이 추후 빅데이터를 다룰 때 신중하고 옳은 판단을 할 수 있습니다.
