Dynamic Programming Algorithms

Dynamic Programming

• recursion sometimes repeatedly solves the same subproblems. (recursive Fibonacci)

< Main Idea >

• Reorganize the computation of subproblems so
  not to solve them over and over again.
  - compute the solution for each subproblem just once.
  - cache the computed solution in a table for future reuse

(하나의 문제를 한번만 풀게 하는 알고리즘 -> 재귀의 단점을 극복하기 위함.)

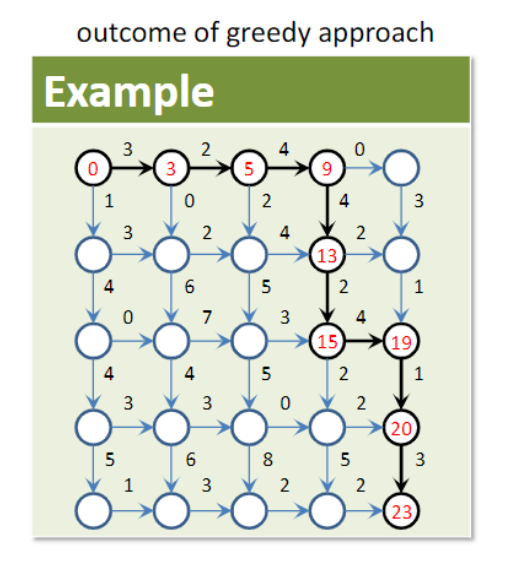
Example: Manhattan tourist problem

• Find route that passes most tourist attractions
  => attraction을 가장 많이 지나는 길 찾기
  
• Graph = (V, E)
  • edges: streets between crossings
  • vertices: streets crossings
  • possible to draw as a regular n x m grid

Directed Graph

• edges point from one vertex to another

• NO directed cycles
  

• Find longest path in DAG, from (0, 0) to (𝑛, 𝑚)

• 이전 계산을 미리 해놓고 저장해놓고 이후 반복 계산 수행을 줄인다.

For general DAGs

• Graph is not a regular grid.

• Each vertex may have arrows to other vertices.

• Order in which to visit vertices.

• When 𝑣 is visited, all its predecessors must have been processed before.

Topological ordering of DAG

• Linear ordering of vertices such that all arrows, which represent dependencies, point forward.

• Arrow from 𝑢 to 𝑣 indicates 𝑢 should come before 𝑣.

• Choose vertex without predecessors.

  • "Remove" vertex and outgoing edges from DAG.
  • Add vertex to ordered list.

• Repeat until no verices left.

DNA sequence alignment

• measure "similarity" between DNA sequences
  

< Hamming Distance >
The number of positions in which the two strings differ.

NOT GOOD for similarity of DNA sequences

• Evolutionary noise( reversal )
• Sequencing and assembly noise

Edit distance

1. Edit distance between two strings

   • Minimum the number of edit operations to transform the first string into the second string.

   • Also known as Levenshtein distance.

2. Edit operations

   • Insertion of a symbol (+)

   • Deletion of a symbol (-)

   • Substitution of a symbol by another (|)

• How to compute(minimum) edit distance?
  • by translating this problem into the Manhattan tourist problem
  • by representing an alignment of two strings as a graph.

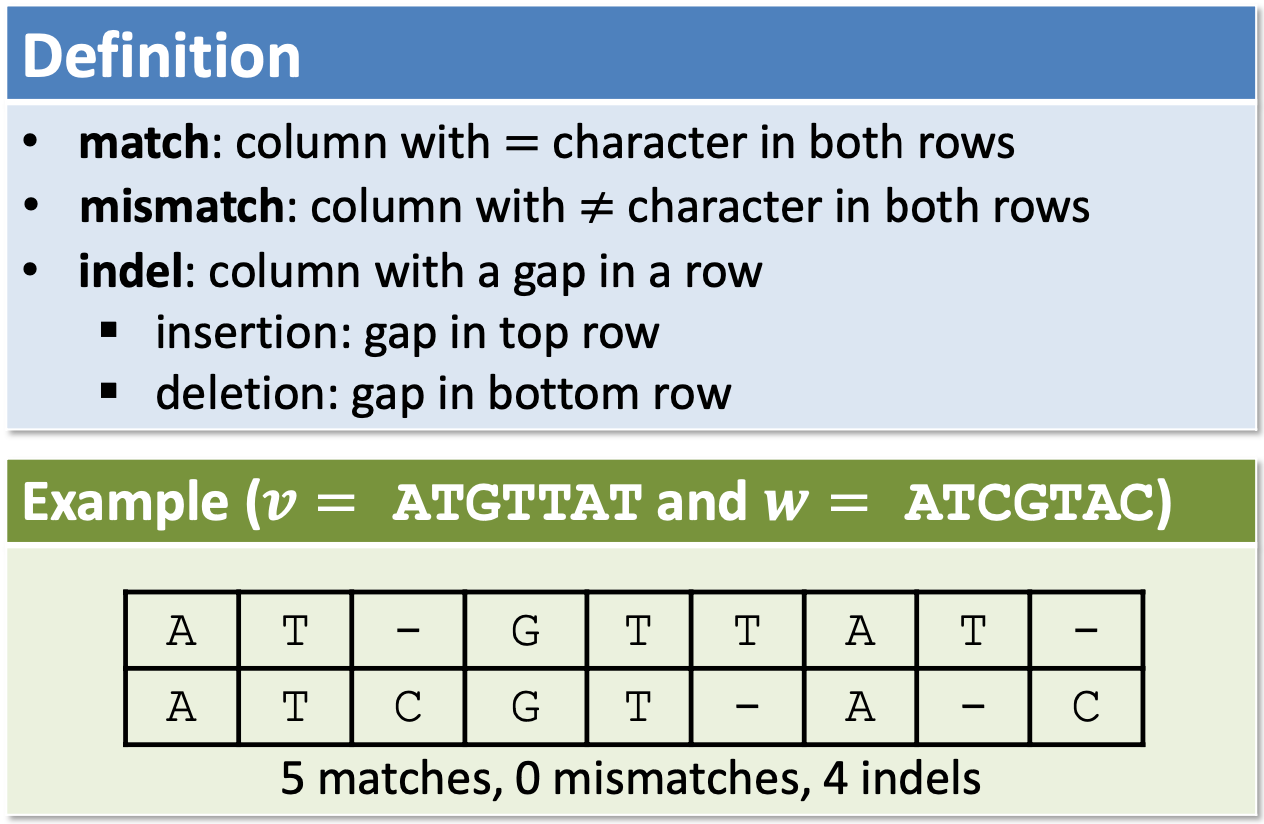
Representing alignments
tring 𝑣 (length 𝑛) and string 𝑤 (length 𝑚)

• first row has characters of 𝑣 in order
• second row has characters of 𝑤 in order
• gaps interspersed in different places

⭐️ NO COLUMN has GAP in both ROWS. ⭐️

1. strings as integer lists

• The number of characters up to position.

2. Integer lists as matrix

   • Combine row representation

3. path represents alignment

Edit Graph

• n x m grid with →, ↓, ↘︎, arrows.
• path in edig graph corresponds to alignment.
• edge on path: column in alignment matrix.

Scoring function

• Used to analyze merit of alignment
  Merit-high merit for alignments with more matches
  

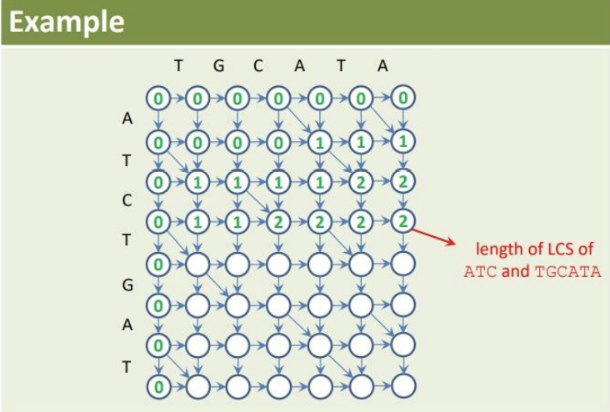
Longest common Subsequences(LCS)

• Find Longest Common Subsequences(LCS)
• Length of LCS = ( A의 길이 + B의 길이 - Edit Distance(A, B)) /
  2
  
• Only insertions and deletions are allowed.
• Substitutions are not allowed.
• ↘ edges for non-matching symbols are removed
  

Example:

1. Weights on edges in edit graph

   • 왼쪽, 아래로 움직이는건 weight 0
   • 대각선 matching symbol만 weight + 1

2. LCS problem is to find longest path in edit graph.

3. Use Dynamic programming
   → So to be able to reuse previous computaion.

→ 이전 값을 계산해놓고, 다이나믹 프로그래밍 maximum값을 선택한다. (Greedy apprach)

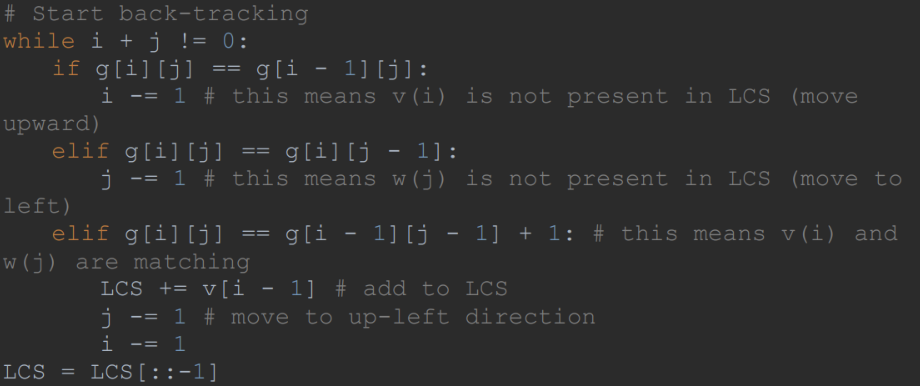
< Backtracking >
LCS 길이를 구했다면, backtracking을 통해 정확한 염기서열을 추적할 수 있다.

• if si,j = si-1,j then bi,j = ↑
• if si,j = si,j-1 then bi,j = ←
• if si,j = si-1,j-1 then bi,j = ↖︎

< Time Complexity >

• Computing s(v,w)
  length of LCS = n*m

• Reconstruction LCS = n + m
  
  Loop가 stop되는 조건이 n+m=0 이므로, 총 while는 n+m 만큼을 연산을 수행하게 된다.

< Space Complexity >

• Dynamic Programming table takes (n*m) memory
• Table with backtracking pointers takes (n*m) memory

Global sequnce alignment

< Scoring System >

• scoring matrix
  • (k+1) * (k+1) matrix
  • with k size of alphabet + gap symbol
  • matrix(x,y) = score of (x,y) in alignment matrix