Graph Algorithms

What is Graph Algorithms?

Graph G = ( V, E )

• set V of n vertices.
• set E of m edges between vertices.

Degree d(V) of vertex v

• The number of vertices connected by edge to V.
• Σd(v) = 2m

  
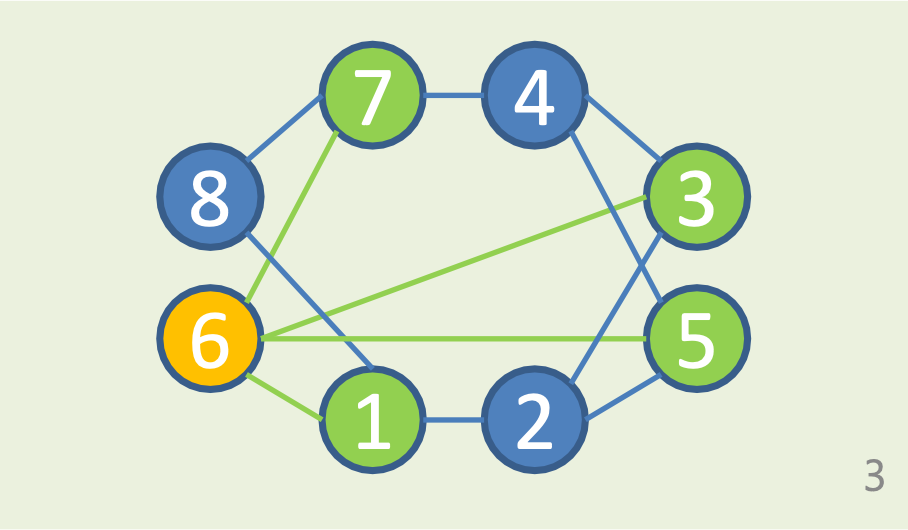
  Edge 기준: 1 → 2와 2 → 1은 서로 같음.
  d(V) 기준: 1 → 2와 2 → 1은 서로 기준(출발점)이 다르기 때문에 개별로 취급!

  즉,Edge는 시작점과 끝나는 점의 순서 상관없이 하나로 취급하기 때문에 총합 d(V)의 1/2!

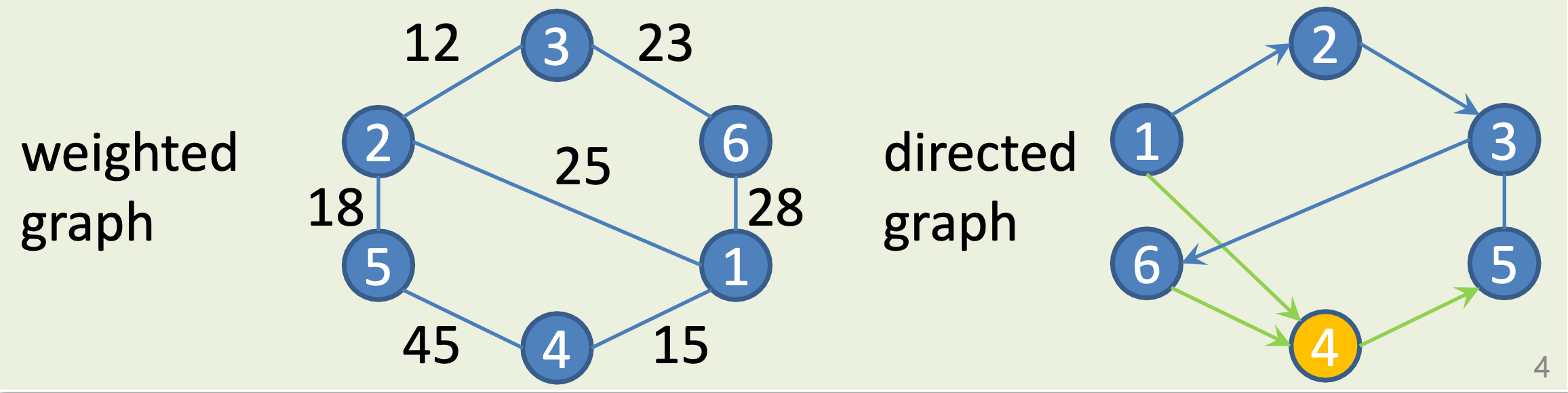
Weighted and Directed Graphs

1. Weighted Graph: edges have weights.

2. Directed graph: arcs point from vertex to other.

• indegree of V = the number of incoming arcs.
• outdegree of V = the number of outgoing arcs.
  

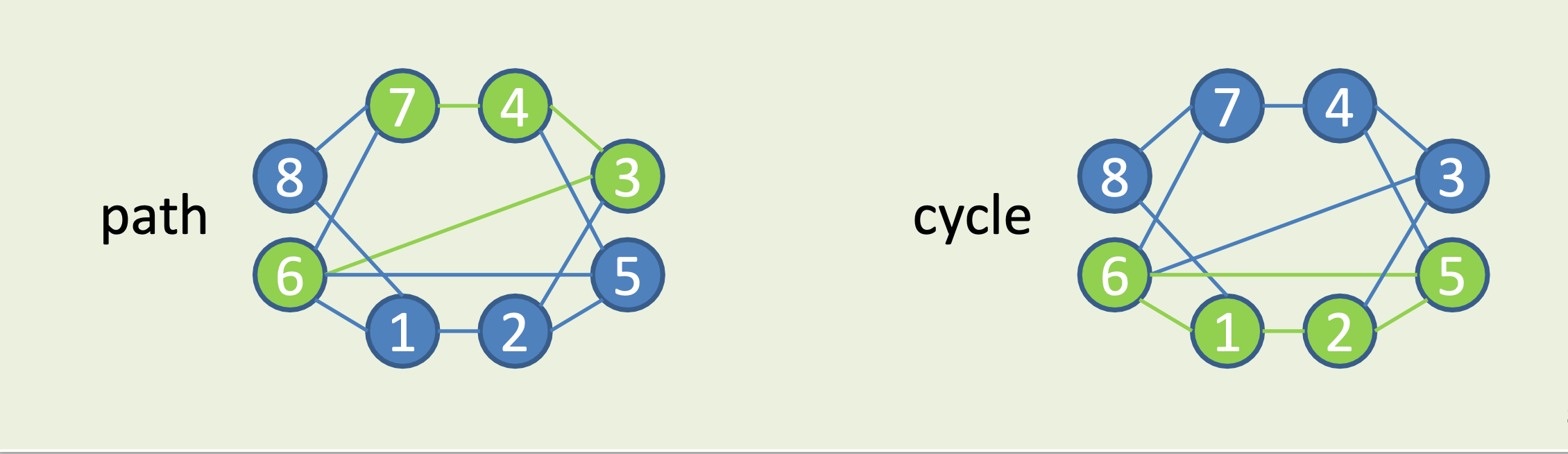
Paths and Cycles

1. Path: continous sequence of edges, no repeated vertices allowed.

2. Cycle: (=closed path) path starting and ending at the same vertex.
   

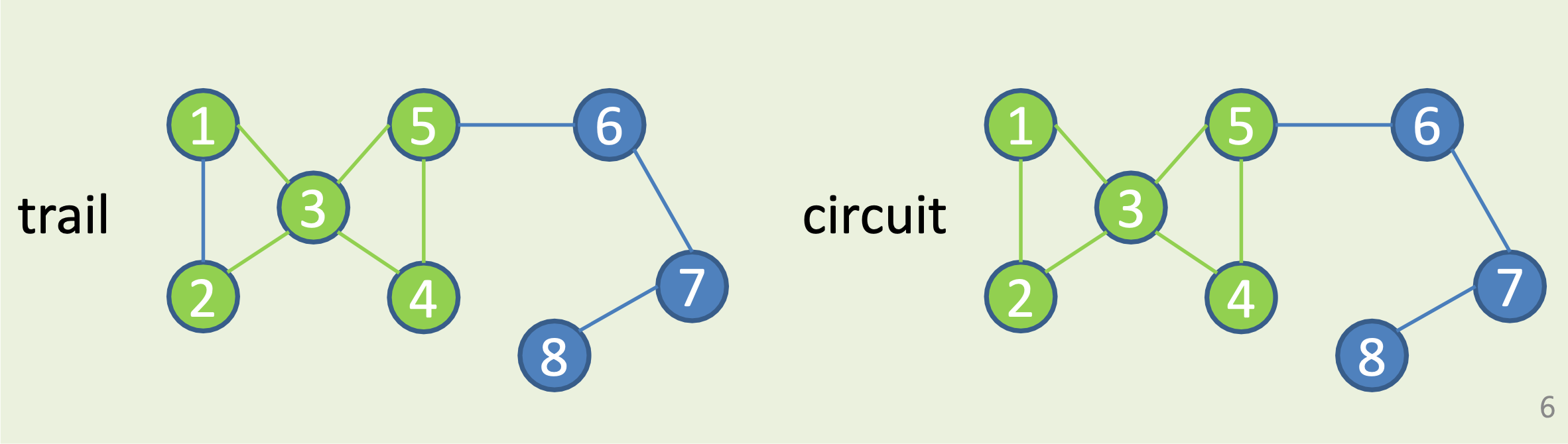
Trails and Circuits

1. Trail: continuous sequence of edges, no repeated edges allowed.

2. Circuit: closed trail = trail starting and ending in same vertex.
   

Connected graphs & complete graphs

1. Connected: Graph 𝐺 exists a path between every pair of vertices.

2. Disconnected: Graph 𝐺 is not connected; 𝐺 can be partitioned into connected components.

3. Complete: Graph 𝐺 is complete if there is an edge between every two vertices.

---

Example: Knight's puzzles and Hamiltonian graphs

1. Knight's Puzzle

Given: WWBB configuration

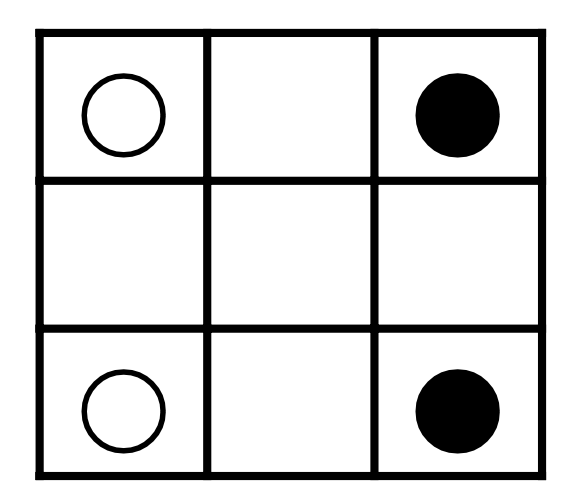
• 3 x 3 chessboard
• 2 white and 2 black knights in corners
• Knights ONLY allows to move
  - 2 rows + 3 columns
  - 3 rows + 2 columns

Question: can knights move from WWBB to BWBW
configuration?
s.t. never two knights on one square

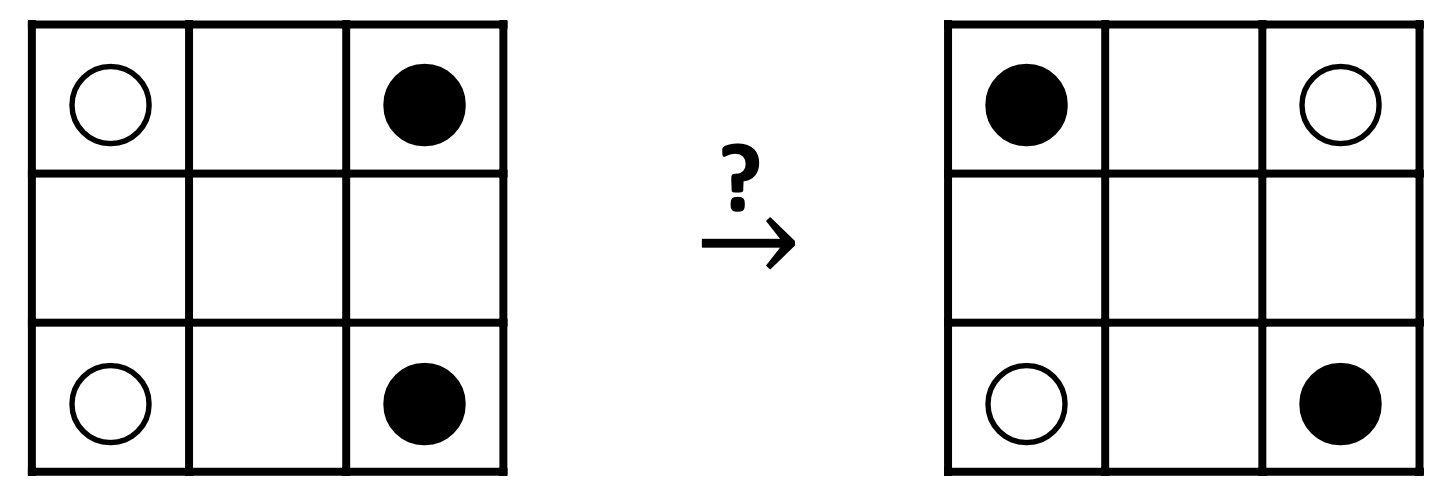
1. Number the Squares
   

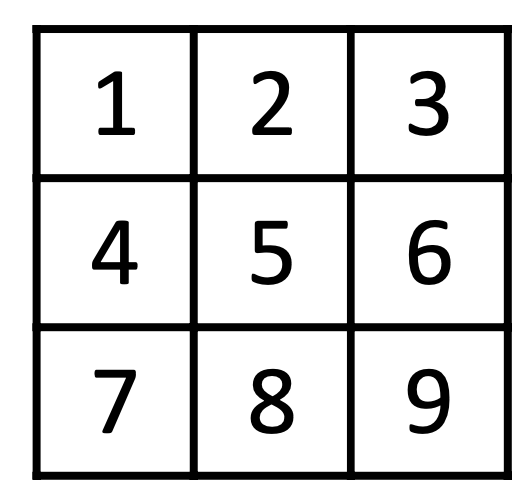
2. Corresponding graph

• vertices are squares.
• edge between vertices if possible to move between squares.
  

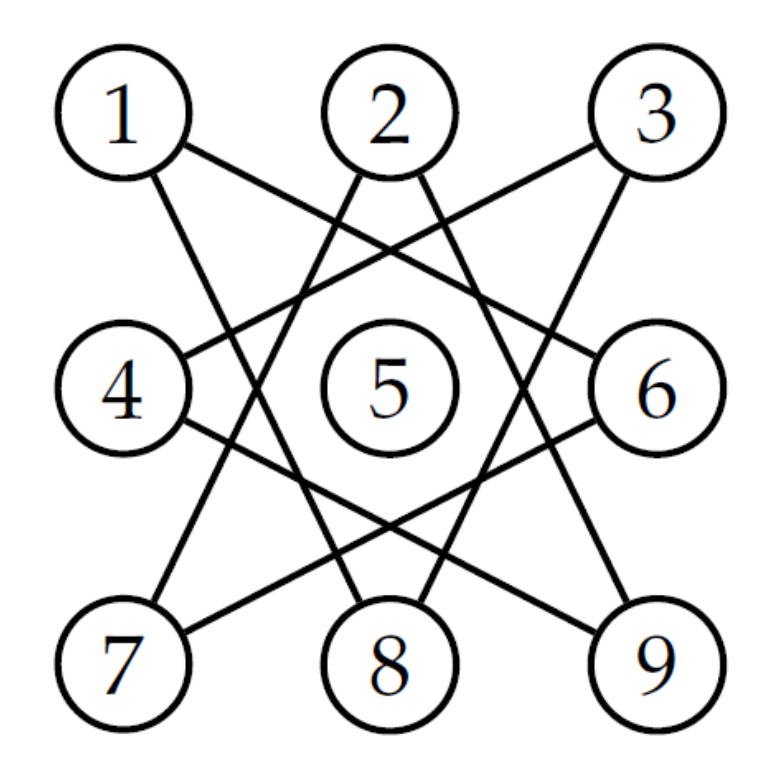
3. Graph Rearranged
   

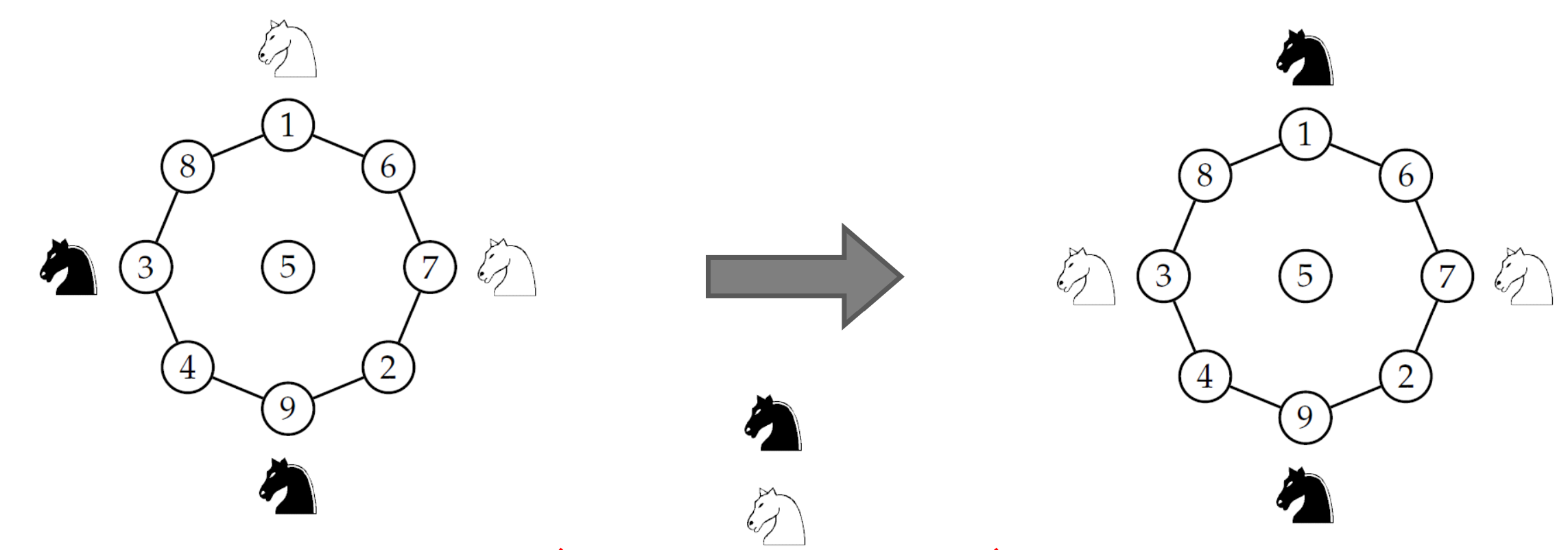
• Knights들은 위의 graph를 기준으로 clockwise or anti-clockwise 방향으로만 움직일 수 있음.

• 따라서, knights cannot move from WWBB to BWBW
  configuration without violating constraint
  (우리가 원하는 결과를 얻으려면, 하나의 자리에 두개의 knight가 있거나, jump해서 자리를 이동해야만 한다.)

2. Hamilton's puzzle: Around the world

• Hamilton's Graph: a closed loop on a graph where every node(VERTEX) is visited exactly only once.

• Is there Hamiltonian algorithm?
  - NO efficient algorithm is known/exist.
  - Intractable problem (다루기 힘든 문제)

Related Problem
→ Traveling Salesman Problem(TSP)

1. in (complete) weighted graph
   • vertices: cities
   • edges: distances
2. find Hamiltonian Cycle of minimum weight

3. Eulerian graphs

Definition of Eulerian Circuit
A circuit which transverses every edge in a graph exactly once.
(즉, 같은 vertex로 돌아와도 상관없음.)

• Hamilton은 every vertex임

Property
Graph is Eulerian if and only if every vertex has an even degree.
(하나의 꼭짓점 당 두개의 꼭짓점만 이어져야 한다.)

STEPS

1. select an arbitrary vertex V.

2. construct an arbitrary circuit by traversing unused edges, til we end up in V again.

3. if the constructed circuit is not Eulerian, then circuit must contain a vertex W that still has untraversed edges.
   

4. use W to construct another circuit using the untraversed edges.

5. combine the two circuits

   • go from V to W
   • go from W back to W
   • go from W back to V

   

---

DNA Sequencing

Shortest superstring problem (SSP)

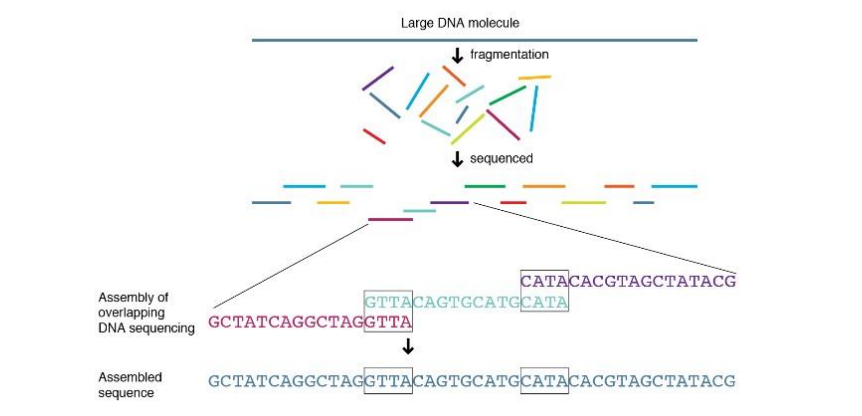
• DNA sequence를 여러조각으로 쪼갠 후(fragmentation) 각 조각들의 염기서열을 분석한 후 다시 assembly하는 과정.

• Overlapping된 염기서열도 존재함.

How to solve

• Define "Overlap" function overlap(Si, Sj)
  → length of longest perfix of Sj that matches with a suffix of Si

• Transform SSP Problem to TSP problem
  → complete directed graph with n verices
  → vertex i is substring Si
  → weight on edge(i, j) is → overlap(Si, Sj)

• TSP = Hamiltonian path problem

• Greedy Approach
  → Repeatedly merge pair of substrings with maximum overlap until one string remains.
  

---

DNA Arrays: sequencing by hybridization(using Hamiltonian path)

• For unknown DNA sequence
• no information about position in DNA sequence
• SSP and SBH very similar as algorithmic problems
• SBH is special case of SSP
  → strings Si have fixed length

(SSP: Shortcut Superstring Problem / SBH: Sequencing By Hybridization)

How to solve

• Overlap of two l-mers p and q
  → p and q overlap(p,q) = l-1
  (= last l-1 chars of p coincide with first l-1 chars of q)

• Given Spectrum(s,l) for unknown s, construct directed graph
  → vertices are l-mers in spectrum(s,l)
  → arc from p to q if p and q overlap
  

• Then one-to-one correspondence between
  → paths that visit every vertex in graph exactly once
  → DNA seqeunces with given spectrum

→ Hamiltonian Path : paths that visit every vertex in graph exactly once.

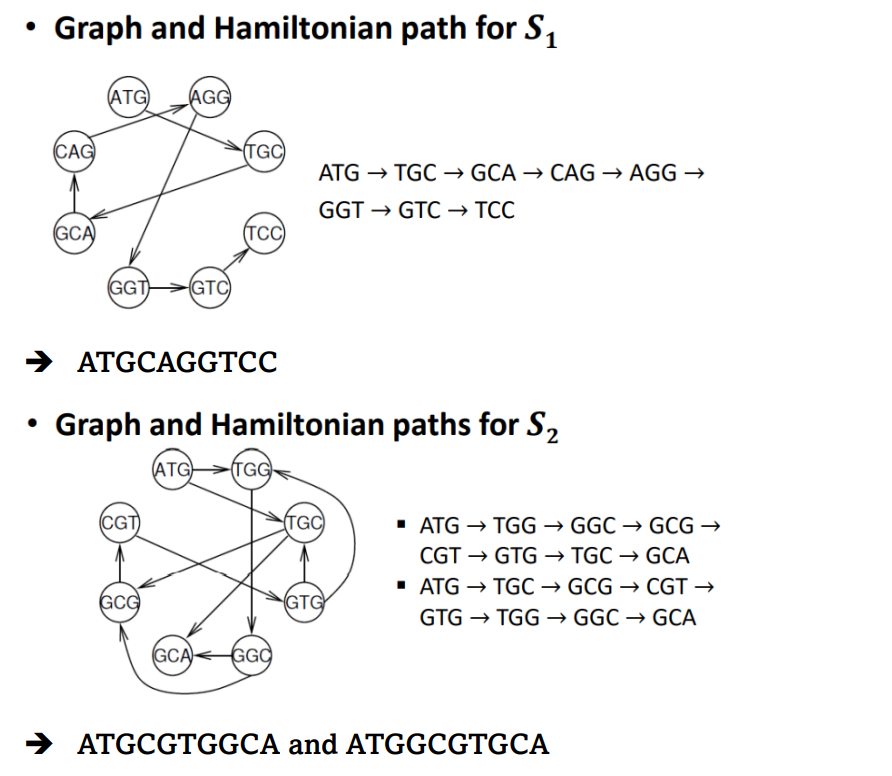
< Example >
1. S1 = { ATG, AGG, TGC, TCC, GTC, GGT, GCA, CAG}
2. S2 = { ATG, TGG, TGC, GTG, GGC, GCA, GCG. CGT}

---

DNA Arrays: sequencing by hybridization(using Eulerian trail)

• construct Graph where EDGES correspond to l-mers
  → instead of vertices(Hamiltonian)
• construct of graph
  - vertices ar all (l-1)-mers
  - arc from p to q if spectrum(s, l) contains l-mer with prefix p and suffix q
  

→ Then, one-to-one correspondence between trails visiting each edge exactly one in graph.

< Example >

---

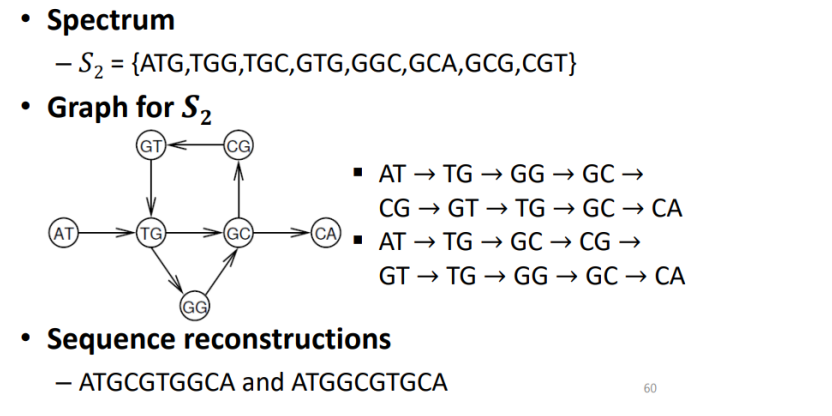
Conclusion

• Use Hamiltonian path when we solve SBH problem
• Not an efficient algorithm
• Not practically useful for large overlap graphs