
Artificial Intelligence
Definition
AI is the field of study that aims at building machines that are as intelligent as people.
→ One way to work towards that goal is through the use of explict programming.
(Python, Java, C++, C, Perl, Bash)
→ Need to specify every detail of particular action in exactly the correct format.
- Explicit Programming

- Machine Learning
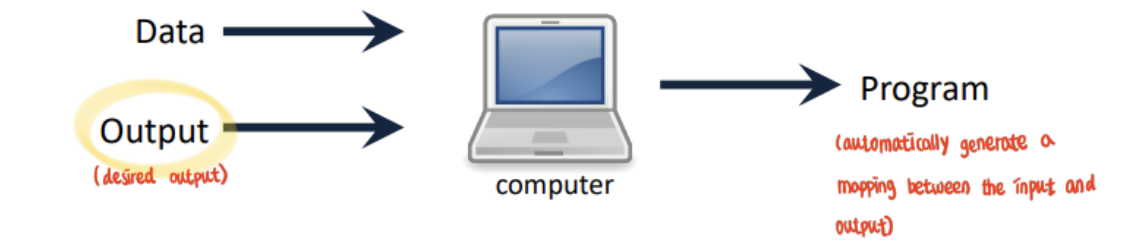
Output = desired output
→ Automatically generate a mapping between the input and output
Machine Learning
Definition
field of study that aims at giving machines the ability to act without being explicitly programmed.
- Example : Virtual Doctor, Web search, Photo tagging, Digital Butler, Spam Detection, self,-driving cars.
Learning Algorithm
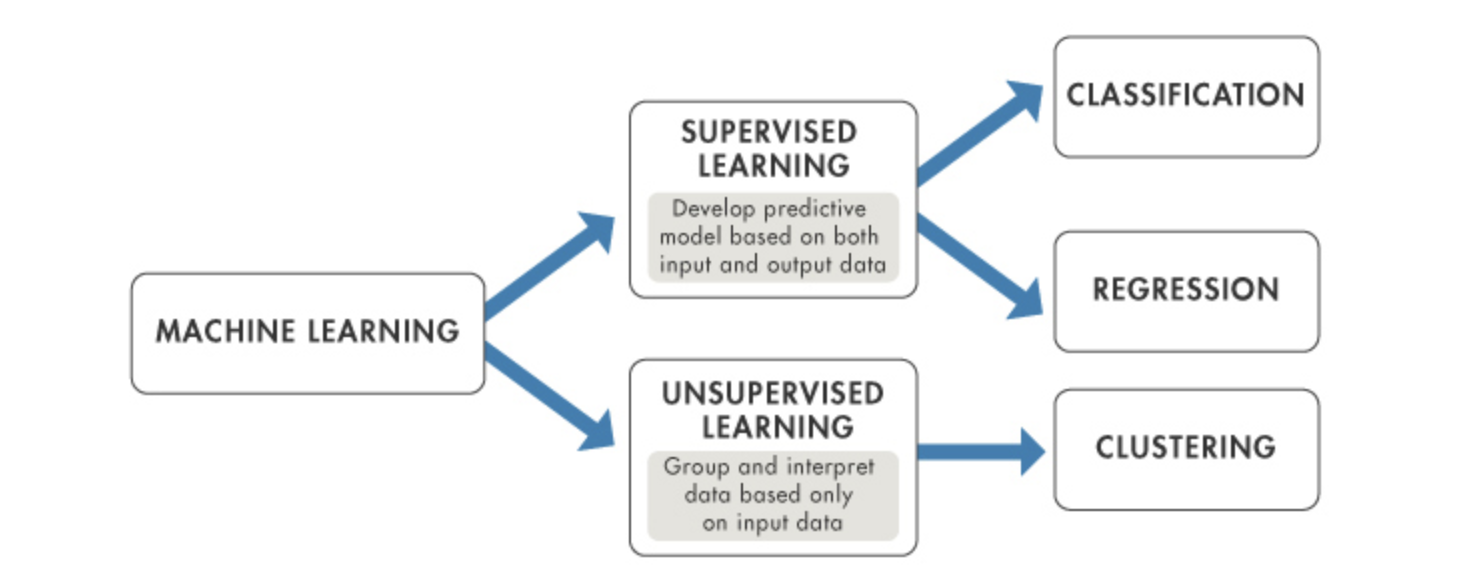
1. Supervised Learning
Learning algorithm gets access to manually labeled examples (help of human access)
< Prediction of House prices based on historical data >
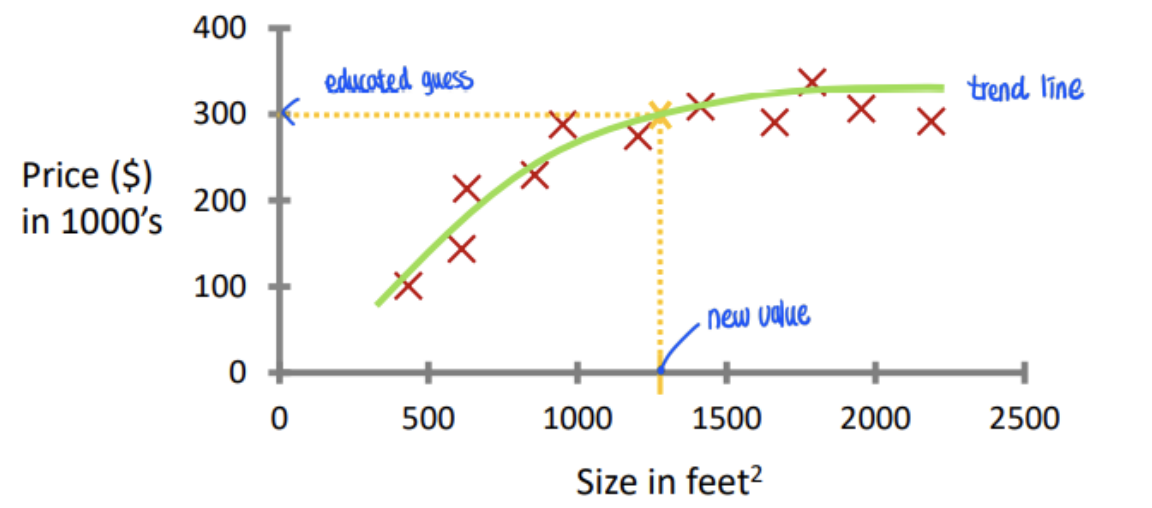
→ Using Regression, Prediction of continous valued output.
< Prediction of the nature of a tumor based on historical data >
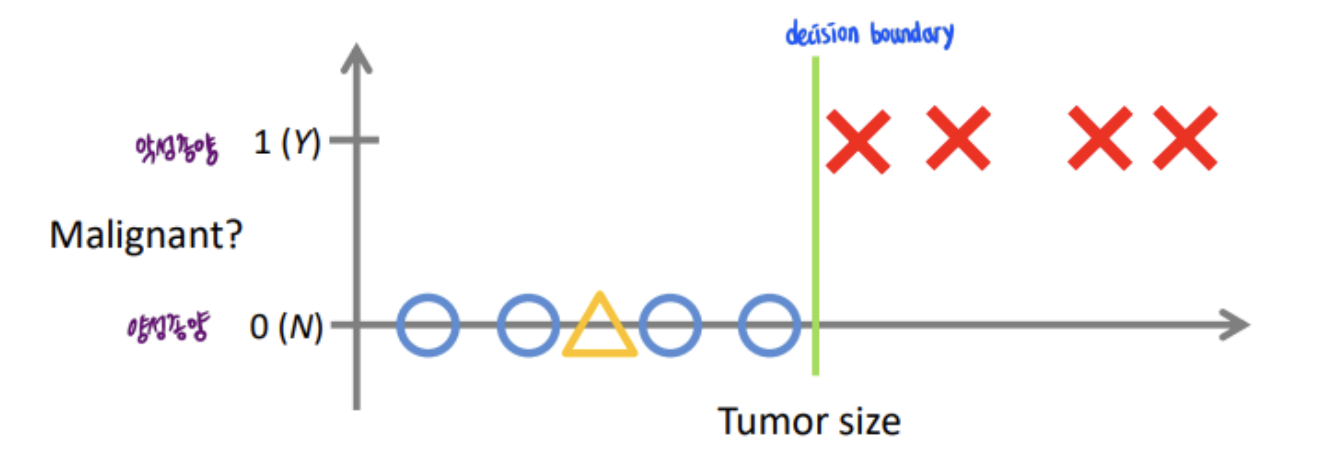
→ Classification : Prediction of discrete-valued output.
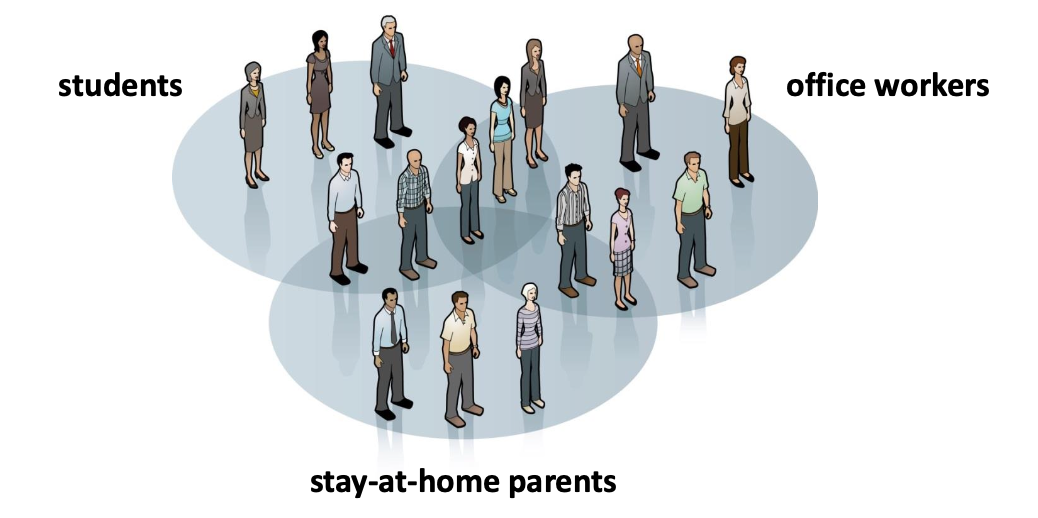
2. Unsupervised Learning
Learning algorithm gets access to non-labeled examples, and needs to find structure and semantics itself, typically through clustering
Problem features
-
attributes that charaterize the problem at hand, used as an input for learning algorithms
-
Examples
- size
- floors
- age
-
Multiple features are typically aggregated(집계된) into a feature vector
Features can be constructed manually or automatically
- Typical Machine Learning Approach
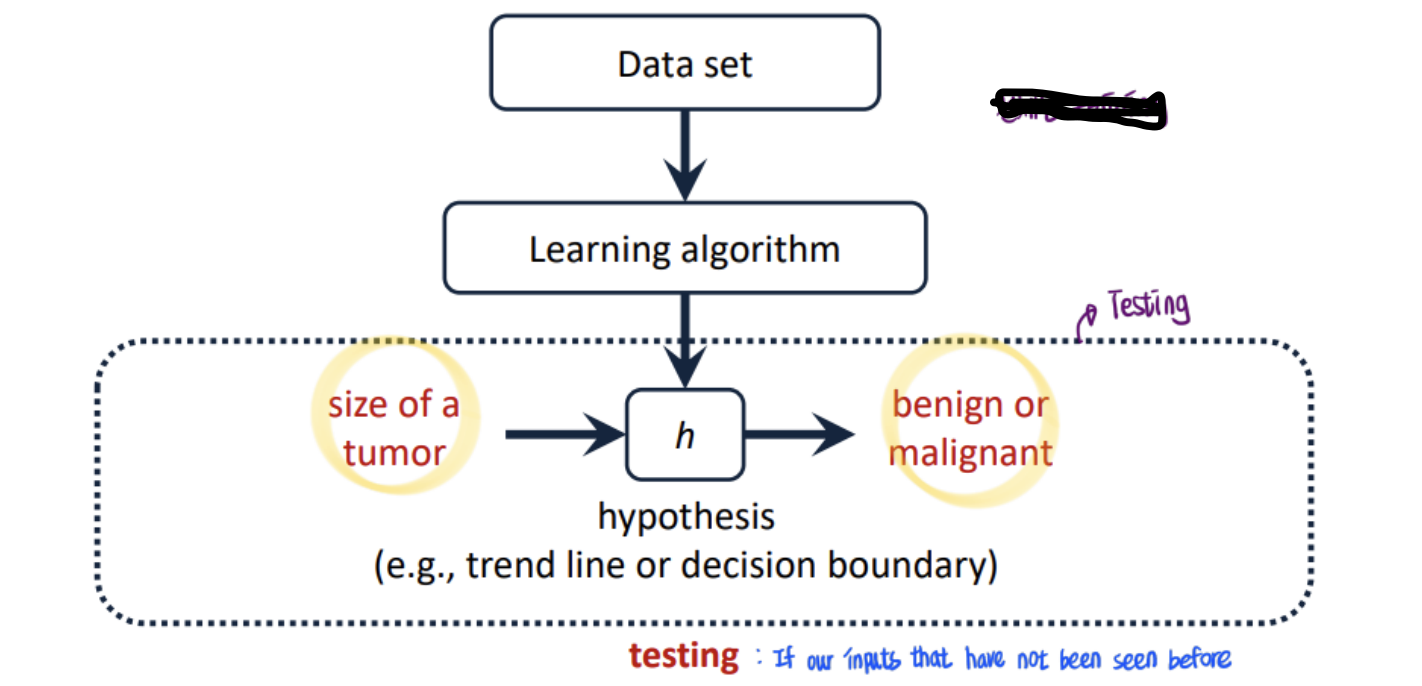
(Supervised Learning → give labeled dataset as data set) - this whole process called 'training'
- Hypothesis(trendline) : Result of training
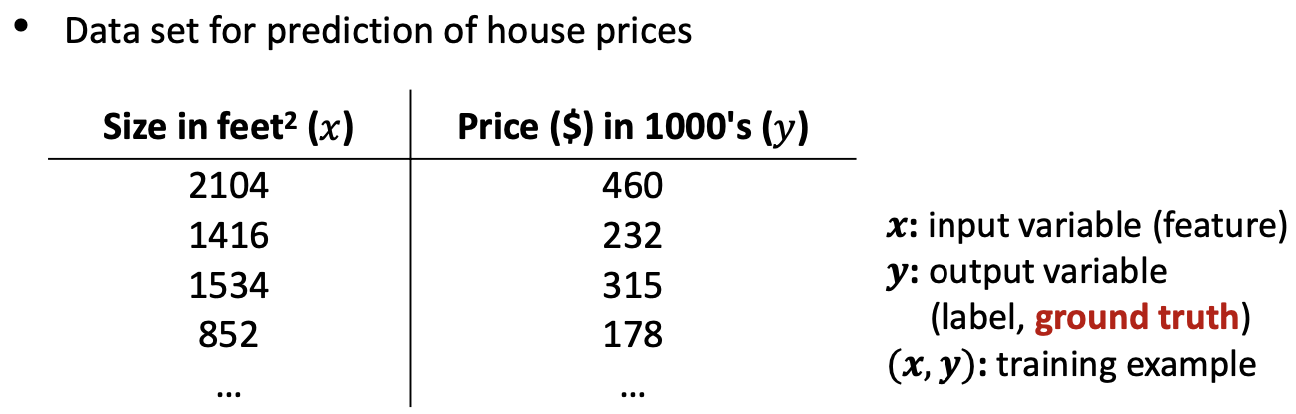
- Testing: using inputs that have not seen before
- Feature : size
- predicted result : estimated~
Hypothesis
1. Univariate(single feature)
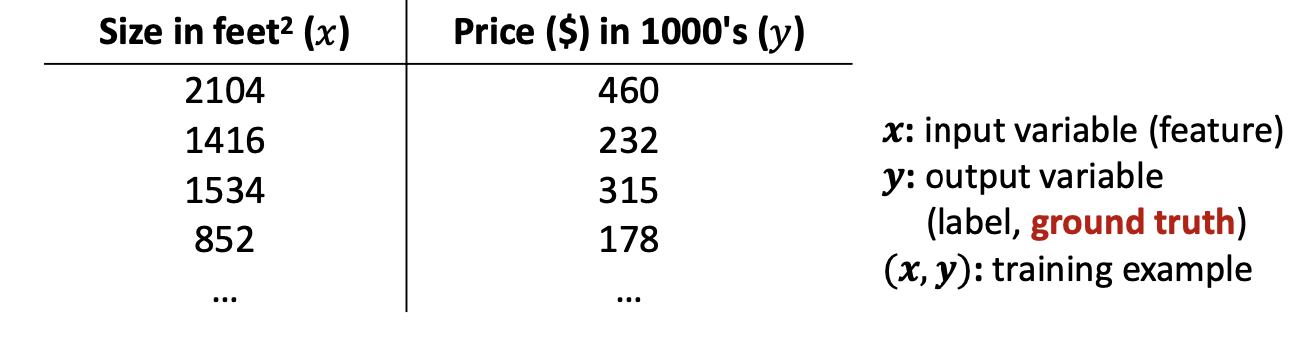
여기서 (x,y)는 hypothesis를 세우기 위한 example이다.
- hypothesis : linear trend-line → parameter: x의 계수
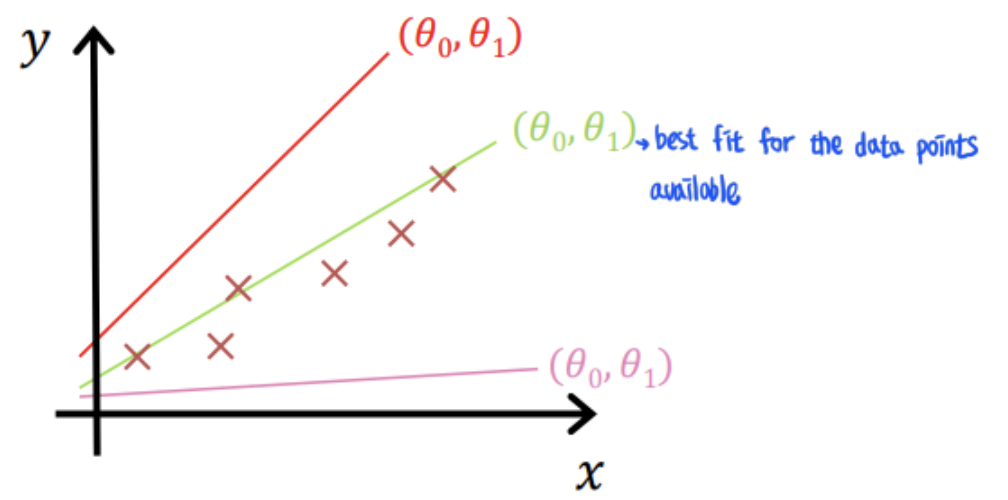
How to choose the 계수 do to have good prediction?
→ Trend line이 training set에 근접하도록 계수(parameter)를 골라야한다.
How to measure closeness with trendline and training set?
→ By using means of a cost or loss function(=prediction error)

Cost function
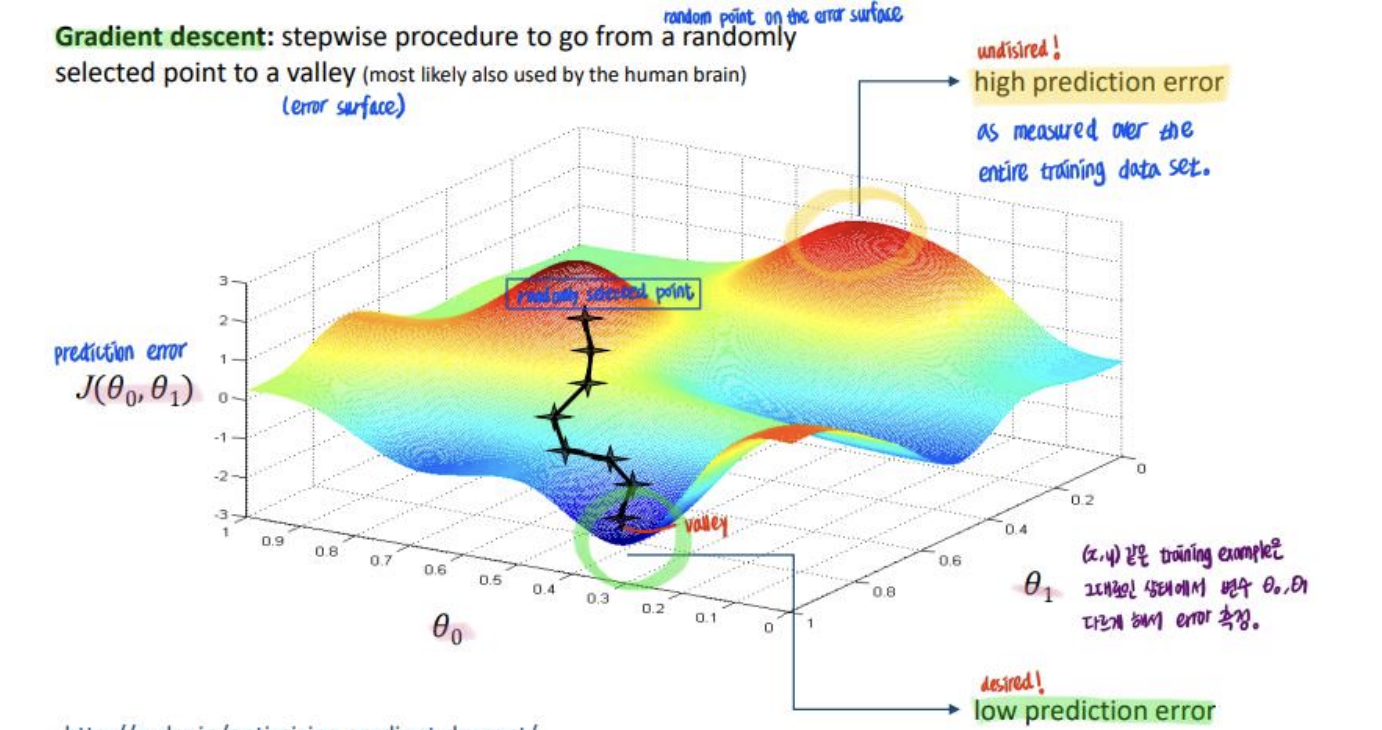
Gradient descent: stepwise approximate procedure to go from a randomly selected point to a valley.
- (x,y) 같은 training example은 그대로인 상태에서 계수들만 다르게 해서 error 측정.
- Parameter을 trendline과 output값들이 가까워지는 걸로 바꿔가면서 추적함
Gradient Descent for Finding Local Minima
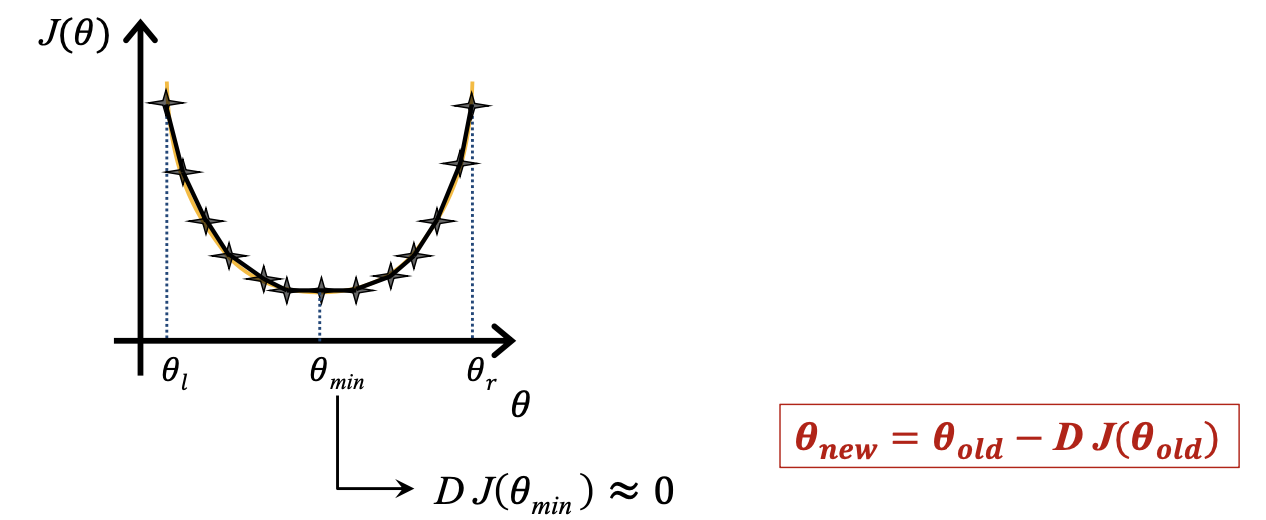
Mathematical property
- decreasing J(⍬): neg. derivative
- increasing J(⍬): pos. derivative
How to find minimum 세타?
- select random ⍬ value
- repeatedly update ⍬ value
Derivative of ⍬minimum almost equals to 0.
Result
- Initial ⍬ to the left of the minimum: neg. derivative → ⍬ moves right.
- Initial ⍬ to the right of the minimum: pos. derivative → ⍬ moves left.
Gradient Descent for Univariate Linear Regression

Gradient descent는 걍 minmum 값을 찾을때까지 계속 iteration.
- Gradient descent에서 미분계수부분이 0이 되는 순간이 → ⍬min = ⍬j 일 때이다.
- ⍺(learning rate)는 여러번 해보면서 사용자가 직접 손봐가면서 찾아가는 변수이다.(보통 이런 변수들을 hyperparameter라고 한다.)
2. Multivariate Linear Regression

Underfitting and Overfitting
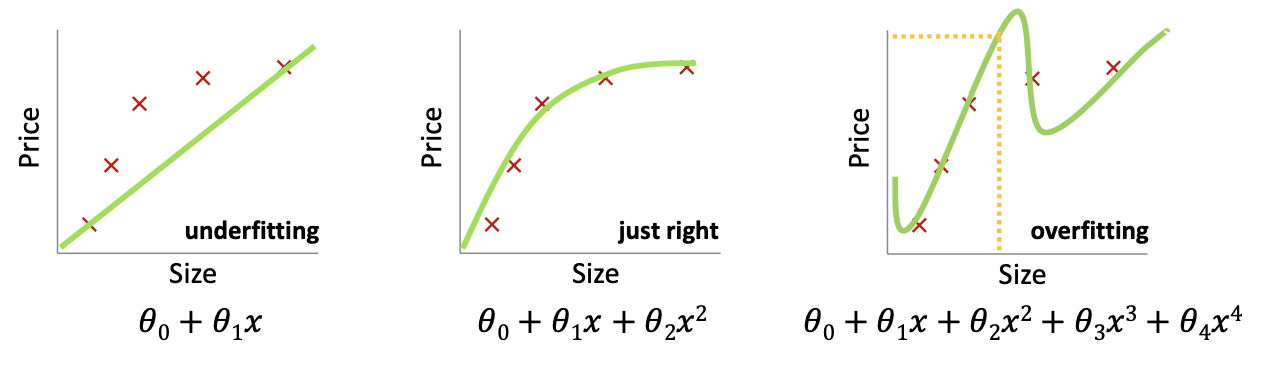
- when we have too many features, the learned hypothesis may fit the training set very well
- but may fail to generalize to new inputs
- may fail to predict representative prices for new inputs.
How to address overfitting
-
reduced the number of features
→ manually or automatically(PCA/SVD) -
Regularization
→ keep all the features, but reduce the magnitudes of 𝜃𝑖
→ that way, each feature can only contribute a bit to predicting 𝑦 -
Small values for parameters
→ "Simpler and Smoother" hypothesis
→ less prone to overfitting
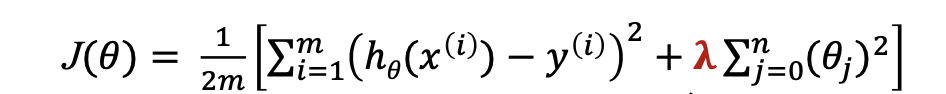
→ Regularization Parameter exist
influences what part to minimize most: prediction error or model complexity.
λ = 0: least-squared regression
λ != 0: ridge regression
기본 선형모델을 사용하다보면 데이터에 매우 적합되어 극단적으로 오르락내리락하는 그래프 발생
→ 선형회귀의 계수 값이 매우 큰, y = 34152 - 24423x + 234234x^2 이런식으로 나타난다. variance가 매우 큰 경우를 막기 위해 계수 자체가 크면 페널티를 주는 ridge regression리다,
