Exhaustive Search Algorithms

What is Exhaustive search

• A technique for problem solving that examines every possible alternative
• Brute force search:
  Only results that meet the requirements while exploring all possible cases.

Examples

1. Change Problem
   • Generate all possible coin combination that add up to the change M
   • Select combination with smallest #coin
2. Finding Passwords
   • Generate all possible combinations of letters and numbers, up to a certain length N

Properties

1. Intuitive approach
2. Gurantees that a solution can be found
3. Not very efficient
   • Exponential Complexity
   • Factorial Complexity
4. Often uses recusion

Improvement

1. Use of Pruning
   → Allows omitting some alternatives
   

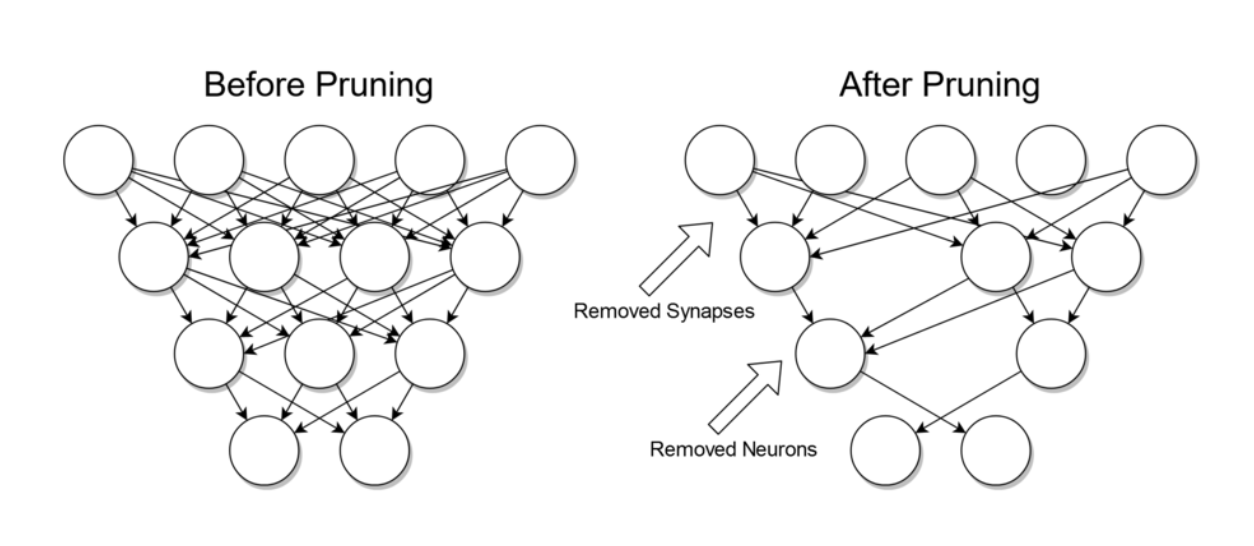
ex ) finding a passward with length N

• omit alternatives with a lengh < N

Exact string matching

• Find occurences of pattern P in text T
• Example: pattern search in biological sequences
  ( Finding origins of replication )

1. Exhaustive Approach

• Try out all possibilities (brute force approach)
  
• Running Time: O(m(n-m+1))
  (alignment: n-m+1 / checks per alignment: m)
  

• Worst case: ⍬(m(n-m+1)) → P does not occur in T
• Best case: ⍬(m) → T starts with P

2. Boyer-Moore-Horspool algorithm

• Improvement upon exhaustive string search by integrating two ideas

  1. Compare P with T from right to left (한 글자씩 비교)
     Shift P from left to right
  2. At character mismatch, shift P over > 1 position
     Results in speed-up of the algorithm by pruning

• Worst case is O(nm) but very fast in practice

< First Idea >

• shift one position to right until match found.

< Second Idea >

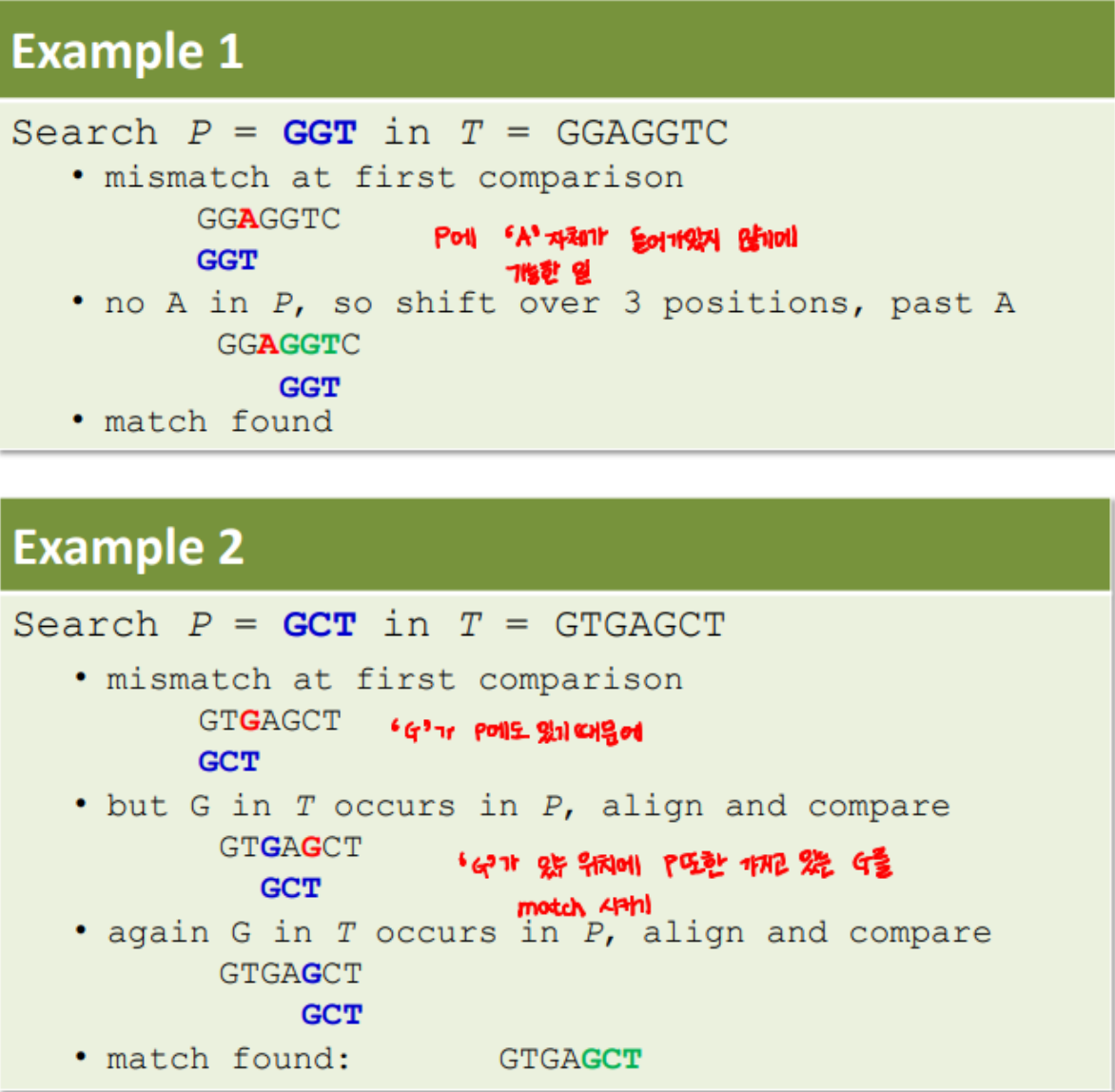
• Then, how to compute the shift distance in practice? (c.f. Example2)

For each character alpha,

Determine the rightmost occurence of alpha in P to the left of P[m-1]

Store distance between rightmost occurence of alpha and P[m-1] as shift distance.

• S → distance between (the rightmost occurence of a particular character) & (the last character of the given pattern P)

• Shift over S[G] = 2 positions, to align G

• Mismatch of A in T and T in P

• Shift over S[C] = 5 positions, past C

• Shift over S[A] = 4 positions, to align A

• Shift over S[T] = 1 positions, to align T

• Shift over S[A] = 4 positions, to align A

• Shift over S[T] = 1 positions, to align T

• Match found!

• m-1-k → Distance between last character of P and rightmost occurance of P[K]
• Perform a shift == PRUNING

3. Rabin-Karp algorithm

• Fingerprinting(Hashing)
  A procedure that maps an arbitrarily large data item to a much shorter bit string(fingerprint)

Simplecheck

• does not consider the full pattern 𝑃
• but only one aspect of 𝑃 → fingerprint or hash

Ideally

• simple check can be performed in θ(1) (≪θ(𝑚))
• simple check eliminates most positions (pruning)

Example

1. Parity check (parity of a bit string)
   • 0 → when the number of '1' bits in the bit string is even
   • 1 → when the number of '1' bits in the bit string is odd
   • search 𝑃 = 0011 in Ƭ = 0001001000
   • 𝑃 has parity 0
   • each Ƭ[i..i+3] has parity 1, except position i = 3 (1001)
   • 7개의 fragment 중 6개의 패턴들이 지워질 수 있는 가능성이 생긴다.

< Time Complexity of Getting Parity>
1. Determining parity of 𝑚 bits costs → θ(𝑚)

• Compute parity of 𝑃 and 𝑇[0..𝑚−1] → θ(𝑚)
• For each position i, cost of determining parity is θ(1) in each step

< Result >
Total Time complexity: θ(𝑚1(n-m+1)) → Effectiveness is not that great

• m : m개의 글자 하나씩 확인해서 1 개수 세기
• 1 : reuse하기 때문에 처음에 parity 계산하고 다음 alignment에선 cost가 1
• n-m+1 : 나올 수 있는 T의 alignment 개수, 비교해야하는 alignment 개수

< Problem >
Too many substrings in 𝑇 share same fingerprint

2. Improved Fingerprint - hashing
   * check whether the hash of the given pattern P is equal to the hash of the current alignment.

< Requirements for fingerprint >
A. Map bit strings of length m on q is differnent with fingerprint ⭐️⭐️⭐️

B. Uniform distribution over q fingerprint → 해시 값이 균일하게 분포되지 않으면 더 많은 해시 충돌이 발생할 수 있다.

C. Easily computed 'in sequence' ( rolling fingerprint )

Rabin-Karp hash function satisfied (A),(B), and (C).

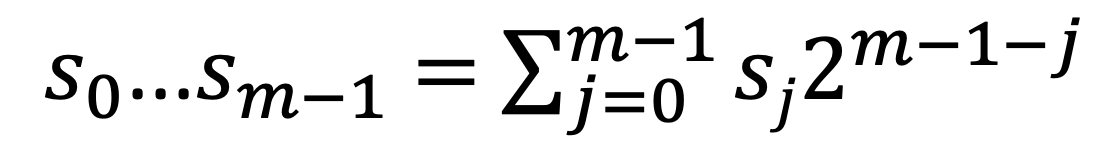
• q selected as a prime number larger than m.
• Keep rest of division by q.
  

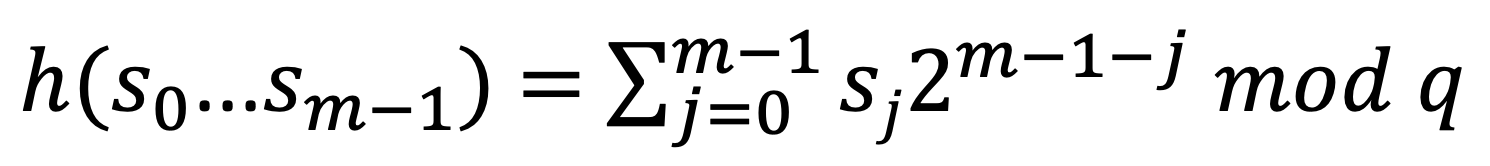
< Formula Following >
⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️⬇️

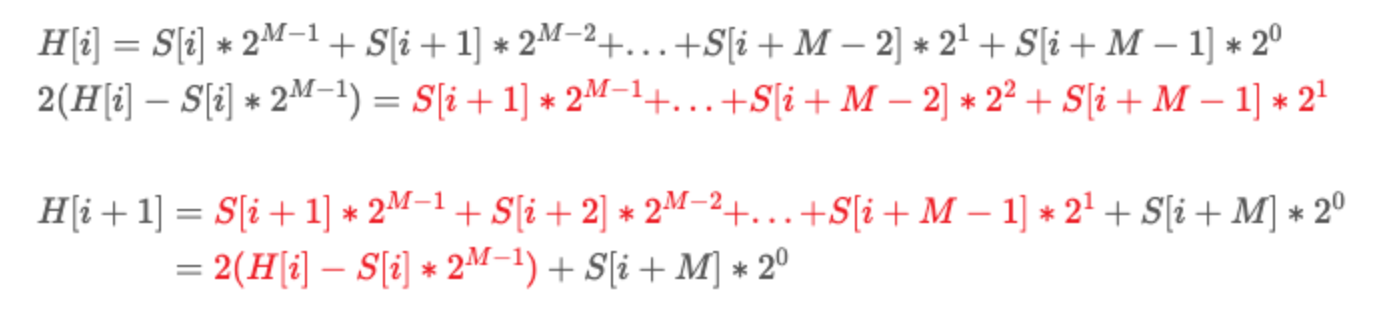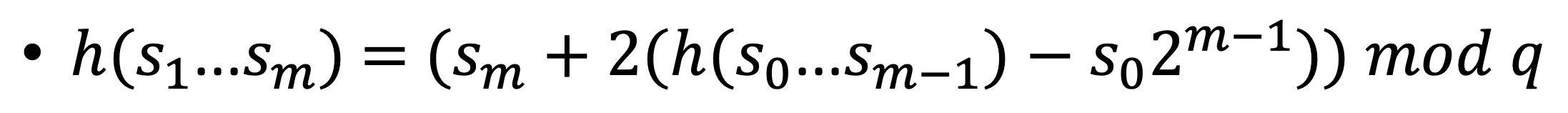
Practical note on string matching

• In python, str.find() ➡️ Based on Boyer-Moore-Horspool