모든 예제 구현이 array-based로 되어있음

1.HEAP

• HEAP은 다음과 같은 특성을 만족하는 Binary Tree이다.

-Shape property: must be a complete binary tree(그래야 ARRAY-BASED로 구현되었을 때 장점을 가짐)

-Order property: 부모는 반드시 자식과 같거나 큰 값을 가진다.(max heap을 일반적으로 그냥 heap으로 퉁쳐서 부름. min heap이면 부모가 제일 작음)

→즉 Binary Search Tree가 아님! BST는 오른쪽 자식이 부모보다 큼

따라서 HEAP 전체에서 가장 큰 값은 루트 노드가 된다.

• HEAP은 complete binary tree이므로(낭비되는 공간도 없고, random access 가능해짐) array로 표현이 가능하다.
• 루트노드를 제거하고 남은 애들로 다시 heap을 만드는 데에 O(logN)밖에 안 걸림 →따라서 Heap Sort는 O(NlogN)이 걸림(각각의 루트들을 제거하고 모아서 큐로 만드므로)
  

---

REHEAPDOWN(for deleteItem) & REHEAPUP(for insertItem)

1. ReheapDown
   • 루트에서 “내려가면서” 비교 연산을 수행함
   • 왼쪽 자식과 오른쪽 자식을 비교하고, 그 중 큰 값이 자기보다 크면 해당 자식 노드와 swap. 그리고 그 subtree에서 다시 ReHeap Down (종료 조건까지 계속 재귀로 ReheapDown하는 것)
   • 삭제 후에 루트에 일단 아무 노드 넣어놓고(보통 마지막 레벨의 가장 마지막 리프 노드) ReheapDown을 반드시 해줘야 함
   • 삭제 후에 루트만 heap을 만족하지 않고, subtree들은 각각 힙을 만족하고 있음. 따라서 루트만 가지고 비교해주면 됨
   • 탈출조건
     • 내려가다가 리프 노드에 도달함
     • 즉 자식 중 루트보다 큰 것이 없음
2. ReheapUp
   • insert를 하면 마지막 레벨에서 가장 좌측의 가장 오른쪽에 새로운 노드가 추가됨
   • 이 때 그 추가된 노드에서부터 “올라가면서” 비교 연산을 수행
   • 만약 얘가 부모노드보다 크면 부모와 swap해주면 됨. 그리고 부모가 더 큰 경우를 만날 때까지 해당 subtree를 계속 재귀로 ReheapUP
   • insert된 그 노드 제외하고는 모두 heap의 성질을 만족하고 있으므로 얘만 비교하면 됨

---

2.Priority Queue

• only the highest-priority element can be accessed at any time
• 기본적으로 함께 저장해야 할 데이터가 2개가 되는 것임 →각 노드 당 2가지 정보를 모두 저장해야 함
  • 우선순위 판단하기 위한 기준(key value)
  • 자체 데이터값
• heap이 만들어지는데 최악도 O(log2(N))을 보장하므로 pq를 구현할 때 보통 heap을 많이 사용함
  • enqueue: items 배열(tree를 나타내는 배열)의 마지막 끝에 아이템을 추가하고 배열(즉 트리)에 대해 ReheapUp,length++
  • dequeue: items 배열(tree를 나타내는 배열)에서 0번째 아이템(루트 노드)를 파라미터를 통해 얻어내고,length- -, 0번째 자리(루트)를 length-1의 아이템으로 일단 채워준 다음, ReheapDown

---

3. Graph (트리보다 상위의 개념)

• Node(vertices) 집합과 노드를 서로 연결하는 edge 집합으로 구성된 데이터 구조
• Formal definition of graphs

• 그래프의 종류
  • directed graph: have a direction, 따라서 각 edge에서 노드의 순서가 매우 중요함!
  • undirected graph: no direction
  • undirected면 directed로 표현됨(상호간 가르키는 거면 undirected이므로. 그 반대는 불가능함)
• 모든 tree는 graph임. tree가 graph에서의 특이한(세분화된) 경우임
  • ex) 루트에서 해당 노드까지 가려면 unique path. 즉, 순환관계 없음, 부모에서 자식으로만 가능(directed)
• Graph Terminology
  • Adjacent nodes: edge에 의해 연결만 되어있다면!! 두 노드들은 adjacent하다고 한다
  • Path: 그래프 상에서 두 노드들을 잇는 노드들의 순서
  • Complete graph: 그래프의 모든 노드들이 서로 다른 노드들과 모두!! 서로 연결되어 있을 때

    • ex) complete directed graph에서 edge의 개수는 N*(N-1) O(N^2)

    • ex)complete undirected graph에서 edge의 개수는 (N*(N-1))/2 O(N^2)

      

  • Weighted Graph: 각 edge들이 value를 가지는 그래프
  • 따라서 각종 성질들을 조합해서 다음과 같이 4가지의 그래프 유형이 만들어짐
    • Directed Weighted Graph
    • Directed Unweighted Graph
    • Undirected Weighted Graph
    • Undirected Unweighted Graph
    • 그리고 이 중에서 Directed Weighted Graph가 제일 넓게 커버/처리할 수 있음
      • 왜냐면 undirected는 상호 연결하면 directed로도 표현가능
      • unweighted는 모두 같은 값을 준다면 weighted로도 표현가능

---

Graph Implementation : Array-based implementation

• Adjacency Matrix[인접행렬]

  • 1D array는 노드들(vertices)을 표현하는 데 사용된다

  • 2D array는 edge들을 표현하는 데 사용된다

  • 즉, 인접행렬이란 노드 번호에 인덱스들을 할당하고 2D배열을 통해 각 edge의 value, 혹은 연결관계를 나타내는 것이다.

    

  • 그런데 상호간 연결이 촘촘하지 않으면(complete graph에 가깝지 않으면) null(zero)값이 너무 많음=⇒ 낭비되는 메모리가 많음

  • 따라서 배열이 아니라! linked list 형태로 만들어보자

• Adjacency List Linked-list implementation
  • 우선 각 노드들을 표현하는 1차원의 배열을 가짐
  • 그리고 각 배열의 칸마다 그 칸에 해당되는 노드의 인접 노드들을 linked list 형태로 연결해줌

• Adjacency Matrix VS Adjacency List

  • Adjacency Matrix

    • dense graph에 좋음 (빈칸이 거의 없으므로 낭비가 없을 거니까)
    • Memory Requirements: O(|v|+|e|)=O(|v|^2) ; 즉 배열의 크기만큼 메모리 필요
    • 배열이라서 random access가 가능함
    • (그래서 알고 싶은 두 노드만 선택하면)두 노드간 연결관계가 빠르게 테스트 될 수 있음

  • Adjacency List
    - good for sparse graph
    - Memory Requirements: O(|v|+|e|)=O(|v|) ; 즉 노드의 수만큼 메모리 필요
    - Vertices adjacent to another vertex can be found quickly(vertex수가 많을 수록 부각됨)

    즉 GRAPH == Adjacency Matrix == Adjacency List 인 거임. 걍 표현 방법만 다르고 같은 거임!

---

Graph Searching

• problem: 그래프의 두 노드 간 경로를 찾음(일반적으로 루트부터 원하는 노드까지)
• methods: DFS(Depth-First-Searching) or BFS(Breadth-First-Search)

1. DFS(Depth-First-Searching)
   • stack을 사용해서(혹은 재귀함수-stack과 밀접한 관련. 재귀함수가 스택구조로 쌓이지만 트리로 구현하는 것처럼) 구현된다
   • 한 노드에서 시작해서, 모든 노드를 가장 깊은 노드까지 방문한 후 형제노드로 갈아탐
   • visit all nodes in a branch to its deepest point before moving up
   • Travel as far as you can down the path
   • 빠르게 모든 경우의 수를 탐색하고자 할 때 사용한다
2. BFS(Breadth-First-Searching)
   • queue를 이용해서 구현된다.
   • 더 깊은 레벨로 이동하기 전에 현재 레벨의 모든 노드들을 방문한다.
   • 두 노드 사이의 최단경로 혹은 임의의 경로를 찾고 싶을 때 사용한다.

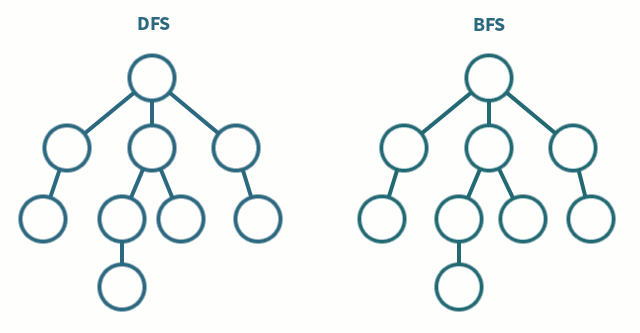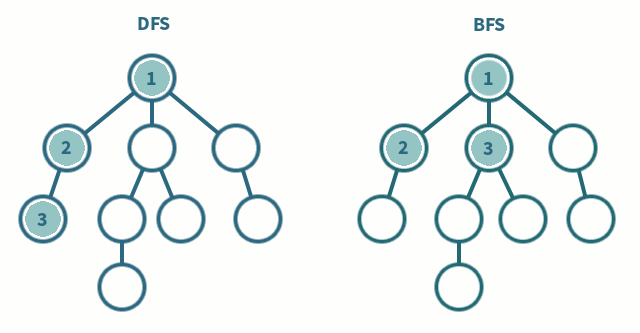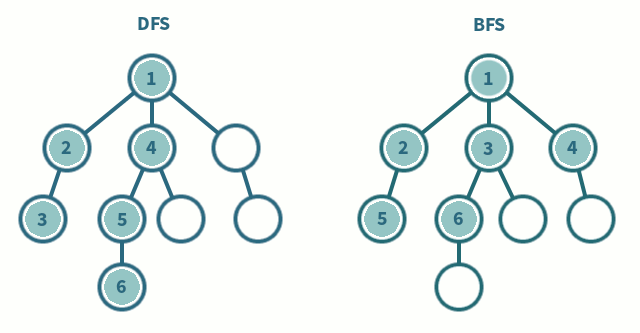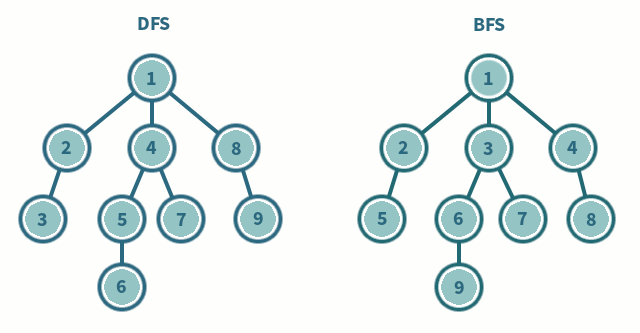
DFS,BFS 과정 및 구현 코드 링크: https://silver-g-0114.tistory.com/35

//위의 링크에서 DFS,BFS의 main에 다음과 같이 되어있는데
//그래프를 Adjacency List로 표현한 것이다
int n, m, start;
	cin >> n >> m >> start;

	vector<int> graph[n+1];
	bool check [n+1];
	fill(check, check+n+1, false);

	for(int i=0; i<m; i++){
		int u,v;
		cin >> u >> v;

		graph[u].push_back(v);
		graph[v].push_back(u);
	}

즉 DFS는 STACK으로 구현되므로

자식2(root의 자식2)(level1)
자식1(root의 자식1)(level1)
부모(root)(level0)

자식2-2(root의 자식2의 자식2)(level2)
자식2-1(root의 자식2의 자식1)(level2)
자식1(root의 자식1) (level1)
부모(root) (level0)

이런 식으로 진행되는 거임

사실 이렇게 스택 구조로 이해하기는 그림을 그리지 않고는 어려움 → 재귀니까 트리구조로 생각하면 훨씬 훨씬 이해하기 쉬움(재귀를 배우면서 느꼈던 것: stack구조는 트리로 생각하면 훨씬 이해 쉽다)

BFS는 큐로 구현되므로

루트(level0)

que.front를 pop하므로

루트의 자식1(level1)	루트의 자식2(level1)	루트의 자식3(level1)

그리고 또 bfs에 들어가면서 front 가 pop 되면서

루트의 자식2(level1)	루트의 자식3(level1)	루트의 자식1의 자식1(level2)	루트의 자식1의 자식2(level2)

---

집합(SETS)

• SET의 속성
  • Sets can not contain duplicates.(집합은 중복이 없다)
  • Sets are not ordered.(집합에는 순서가 없다)
    • →그래서 인덱스 등으로 접근 못 함(random access 불가)
• When implementing SETS, although sets are not ordered, why is SortedList ADT a better choice as the implementation structure for the implicit representation? → 중복체크시 정렬이 되어있으면 확인이 편하므로