알고리즘
문제를 해결하기 위한 여러 동작들의 모임
알고리즘의 3대 조건
-
0개 이상의 input
-
0개 이상의 output
-
유한 시간 안에 끝나야 한다. (유한성)
시간 복잡도 (Time Complexity)
문제를 해결하기 위한 알고리즘이 걸리는 시간과 입력한 함수 관계로, 연산 횟수(시행 횟수) 를 기준으로 한다.
중요한건 실제 걸리는 '시간', 예를 들면 5초, 10초가 걸린다의 시간이 아니라는 것이다.
이 문제를 해결하는데 10초가 걸린다 x
이 문제를 해결하는데 100번의 계산이 필요하다. o
공간 복잡도
문제를 해결하기 위한 알고리즘에 필요한 메모리 공간의 양
총 필요 저장 공간
- 고정 공간 (알고리즘과 무관) : 코드 저장 공간, 단순 변수 및 상수
- 가변 공간 (알고리즘 실행과 연관) : 실행 중 동적으로 필요한 공간
- S(P) = c + Sp(n)
- c : 고정공간- Sp(n)Sp(n): 가변 공간
빅오 표기법을 생각해 볼 때, 고정 공간은 상수이므로 공간 복잡도는 가변 공간에 좌우된다.
Big-O notation
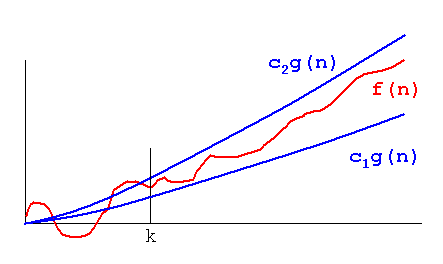
점근 표기법
어떤 임의의 N(커다란 수, k이상)에 대해서, 최소 이 정도 속도는 보장된다는 성능 상한선.
알고리즘 효율성은 값이 클 수록, 즉 그래프가 위로 향할 수록 비효율적임을 의미한다.
빅-오 : 상한선. c2g(n)
빅-세타 : 상한선, 하한선 사이
빅-오메가 : 하한선. 위 그래프의 c1g(n)
다만 최악, 최선의 경우를 나타내는 것이지 알고리즘의 성능이 그렇다는 것은 아니다.
특징
-
상수항 무시 : 입력된 데이터값이 충분히 크다고 가정하기에, 상수한 같은 사소한 부분은 무시한다
ex) O(2N)이 아니라 O(N)로 표기한다 -
영향력 없는 항 무시 : 위 이유와 마찬가지.
ex ) O(N^2 + 2N + 1)이 아니라 O(N^2)만 표기한다.
예시
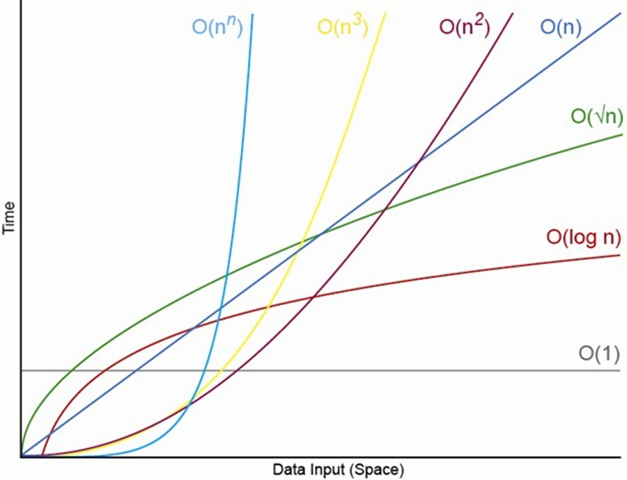
-
O(1) : 입력 자료의 수(n)과 관계없이 일정한 실행 시간을 갖는다. 스택에서 push, pop
-
O(log n) : 초반엔 빠르지만 후반부로 갈 수록 실행 시간이 늘어난다. 이진트리
-
O(n) : 입력 자료의 크기만큼의 실행 시간을 갖는다. for 문
-
O(n log n) : 선형 로그형. 데이터가 2배로 늘 때, 연산 횟수가 2배 조금 넘게 증가한다. 퀵 정렬, 병합 정렬, 힙 정렬
-
O(n^2) : 조합 가능한 모든 쌍을 대상으로 한다. 이중 for 문, 삽입 정렬, 거품 정렬, 선택 정렬
-
O(2^n) : 지수형 빅오. 연산 횟수가 굉장히 증가한다. 피보나치 수열
-
O(c^n) : 최악의 시간 복잡도. 재귀
-
O(n!) : 계승
