알고 넘어가면 좋은 것
1.알고리즘(algorithm)
- 문제를 해결하기 위한 여러 동작들의 모임
- 어떤 기능이 일어나기 위해 내재된/독립된 단계적 명령어들의 집합
1) 좋은 알고리즘의 분석 기준
Correctness : 문제를 해결하는가
Efficiency : 이를 효과적으로 하는가
- 정확성
- 작업량
- 기억 장소 사용량
- 최적성
- 복잡도(빅O 표기법=점근표기법)
2.머신러닝(machine learning)
- 정의되지 않은 데이터를 학습하여 이 경험을 통해 기계가 자동으로 데이터를 학습하고 실행하는 컴퓨터 알고리즘
출처
머신러닝이란 무엇인가?
기계학습
3. 복잡도
점근적 복잡도
- 입력크기가 충분히 클 때, 시간복잡도와 공간복잡도를 분석하는 것.
- 각 알고리즘이 주어진 데이터의 크기를 기준으로 수행시간(연산) 혹은 사용공간이 얼마나 되는지 객관적으로 비교할 수 있는 기준 제시
- O(빅오), Ω(오메가), Θ(세타) 등이 있고, 빅오와 세타표기가 많이 사용된다.
1) 시간복잡도(Time complexity)
- 문제를 해결하는데 걸리는 시간과 입력한 함수 관계로, "연산의 횟수"(시행 횟수)를 센다.
- 상대적으로 불필요한 연산을 제거하여 알고리즘의 분석을 조금 더 간편하게 하는 목적으로 표기하는 방법.
시간복잡도는 '실행시간'으로 하지 않나요?
만약 실행 시간으로 시간복잡도를 계산할 경우, 아래와 같은 단점 발생
- 측정을 위한 완성된 프로그램 필요하다
- 모든 플랫폼에서 동일한 결과를 산출하지 못한다.
-
알고리즘의 성능평가 : 최선,최악,평균 유형(best, worst, average case)
알고리즘 분석시, 평균성능과 최악의 성능이 가장 많이 활용된다. 알고리즘이 복잡해질수록 평균의 경우가 구하기가 어려워져서 최악의 경우로 알고리즘 성능을 파악한다- 최선의 경우(Best Case)
최적의 입력을 한 상태에서 작업을 완료하는데 가장 빠른 시간이 걸리는 것 - 최악의 경우(Worst Case)
최악의 입력을 한 상태에서 작업완료까지 가장 느린 시간 - 평균의 경우(Average Case)
여러가지 다른 경우의 수를 입력하여, 총실행시간을 계산하고 시행횟수로 나눈다.
- 최선의 경우(Best Case)
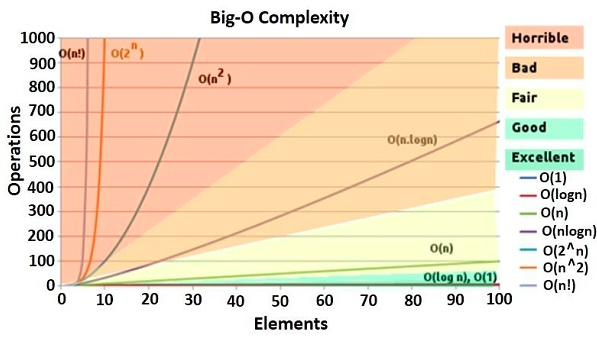
Big-O Notation(빅O표기법)
-
점근적 상한선(Asymptotic upper bound)
-
계수와 낮은 차수의 항을 제외시키는 방법
-
상수는 과감하게 삭제(모두 1이 된다)
-
O(1) : 입력 자료의 수(n)에 관계없이 일정한 실행 시간을 갖는 알고리즘(Constant Time) - 예시 : 배열에서 특정 인덱스 찾기, 해시테이블 추가
-
O(log n) : 초반엔 빠르지만 후반부 갈수록 시간이 증가함 - 예시 : 이진 탐색
-
O(n) : 입력 자료의 크기가 N일경우 N 번만큼의 수행시간을 가진다.(linear) - 예시 : 연결 리스트 순회, 최대값찾기
-
O(n log n) : 선형 로그형, 데이터의 수가 2배로 늘 때, 연산횟수가 2배 조금 넘게 증가한다. - 예시 : 퀵 정렬, 병합정렬 등
-
O(n^2) : 주로 2중 for loop를 사용하여 조합가능한 모든 쌍을 대상으로 하는 경우가 전형적(quadratic) - 예시 : 버블 정렬,삽입 정렬
-
O(n^3) : 3차형(cubic)
-
O(2^n) : 지수형 빅오, '지수적증가'는 무서운 연산횟수 증가를 야기한다. - 예시 :피보나치수열
-
O(c^n) : 최악의 시간 복잡도 - exponential - 예시 : recursion
-
O(n!) : 계승(factorial)
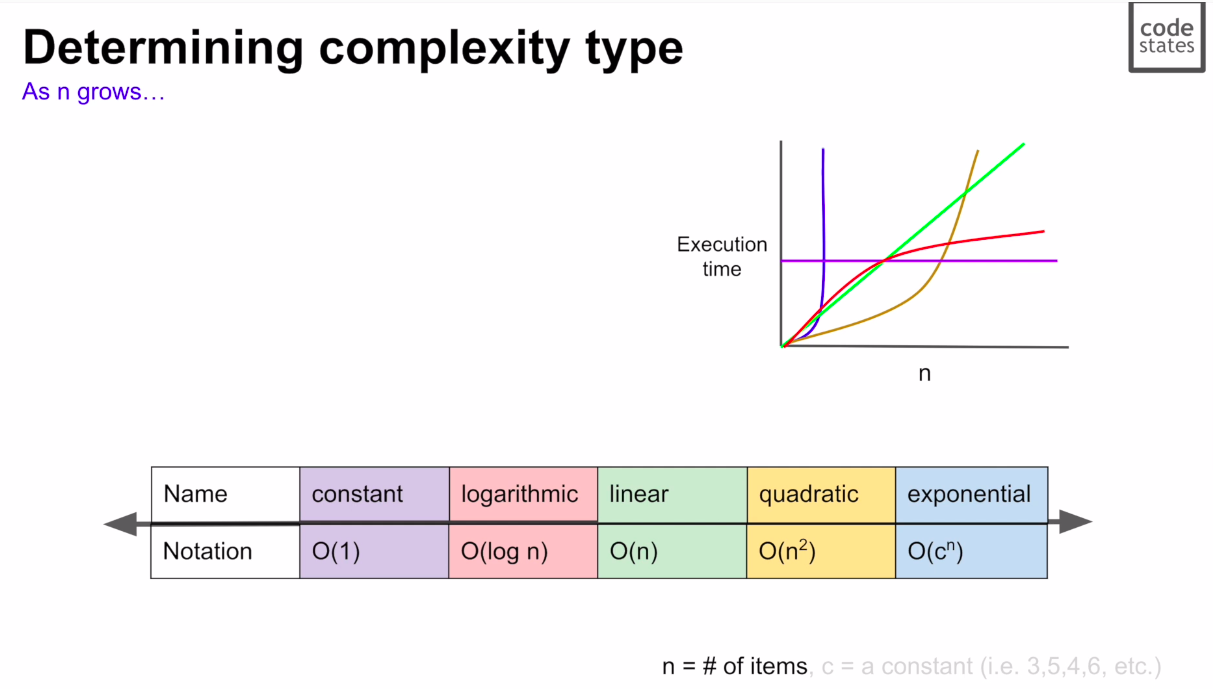
2) 공간복잡도(Space Complexity)
- 프로그램 실행 후, 완료하는데 필요로 하는 자원 공간의 양
- 총 필요 저장공간
- 고정 공간(알고리즘과 무관) : 코드 저장공간, 단순 변수 및 상수
- 가변 공간(알고리즘 실행과 관련) : 실행 중 동적으로 필요한 공간
3) 시간복잡도 vs 공간복잡도
- 시간복잡도는 "얼마나 빠르게 실행되느냐"
- 공간복잡도는 "얼마나 많은 자원이 필요한가?"
- 시간과 공간은 반비례적 경향이 있으므로, 시간 복잡도 위주로 판단한다.
참조사이트
시간복잡도와 공간복잡도(Time Complexity Space Complexity)
[알고리즘] 공간 복잡도
4.자료구조와 시간 복잡도
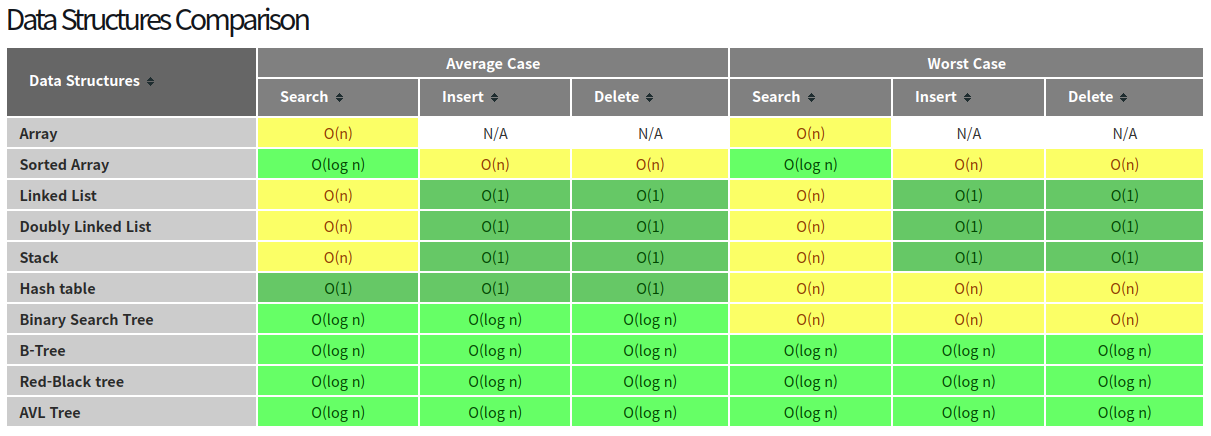
1) 배열(Arrays)
- Lookup(position)/Assign : O(1)
- Insert/Remove/Find(value) : O(n)
2) 연결리스트(Linked list)
- Lookup(position)/Assign/Find(value) : O(n)
- Insert : O(1) → 체크포인트시간으로 내용 보강 - 일반적인 경우는 O(n)
- Remove
- 단일 연결리스트 - head : O(1), middle : O(n)
- 이중 연결리스트 - O(1)
자료구조 사용 시, 고려해야할 장단점(tradeoffs)
각각의 자료구조들은 자기 나름의 장단점을 지니고 있다.
이 자료구조의 장단점을 알아야, 데이터 구조를 사용할 때 조금더 효율적으로 쓸 수 있다.
- 배열 : lookup에 효율적, 추가/삭제에 선형시간복잡도
- 단일연결리스트 : 삽입에 효율적, 룩업과 삭제에 선형
- 이중연결리스트 : 추가/삭제에 효율적, 각 노드마다 이전노드에 대한 정보를 차지하다보니 공간복잡도도 지니고 있다.
3) 트리(Trees)
- Find
- 일반 트리 : O(n)
- 이진 검색 트리 : 왼쪽은 작고, 오른쪽은 크다는 조건이 있으므로 O(log n)
그러나 비균형적인 트리의 경우, 전체 탐색을 진행하기 때문에 O(n)이 시간이 걸린다. = 연결리스트와 다를게 없음. → 최악의 경우를 방지하기 위해, 추가할 때마다 밸런스 조정을 진행한다(3개씩)
정렬된 배열 대신 BST를 사용하는 이유
- 배열은 메모리에서 연속한 메모리(contiguous memory)를 차지한다. 트리는 연속되지 않은 메모리를 차지하고, BST 내에서 진행되는 추가/삭제의 경우 정렬 배열보다는 더 효율적으로 메모리를 사용한다.
자료구조에 대해 자세히 알고 싶다면 이곳 클릭!
그외 참조사이트
위키피디아-시간복잡도
알고리즘과시간복잡도
원문 - 알고리즘 쉽게 이해하기 : 시간 복잡도와 Big-O 표기 → 번역본
stackoverflow
8 time complexities that every programmer should know
