머신러닝 최적화와 경사하강법

최적화와 모형 학습

최적화란?

Loss함수를 정의하고 Loss 함수를 최소화 해주는 모형, 패턴을 찾는 것

Loss함수(손실함수)란?

머신러닝에서 모델이 나타내는 확률 분포와 데이터가 따르는 실제 확률 분포 사이의 차이를 나타내는 함수
즉, 예측값과 실제값 사이의 차이를 나타내는 함수이다

① 회귀 손실함수의 종류

• MAE(Mean Absolute Error)
• MSE(Mean Squared Error)
• RMSE(Root Mean Absolute Error)
• RMSLE(Root Mean Squared Log Error)
• R-Squared(Coefficient of Determination)
• Huber Loss

② 분류 솔실함수의 종류

• Cross-Entropy
• Binary Entropy

Gradient Descent 경사하강법

함수의 기울기(경사)를 구하고, 경사의 반대(하강하는) 방향으로 계속 이동시켜 함수값을 가장 빠르게 하강시켜줄 수 있는 방향으로 반복적으로(iterative) 내려가는 최적화 알고리즘이다

특징

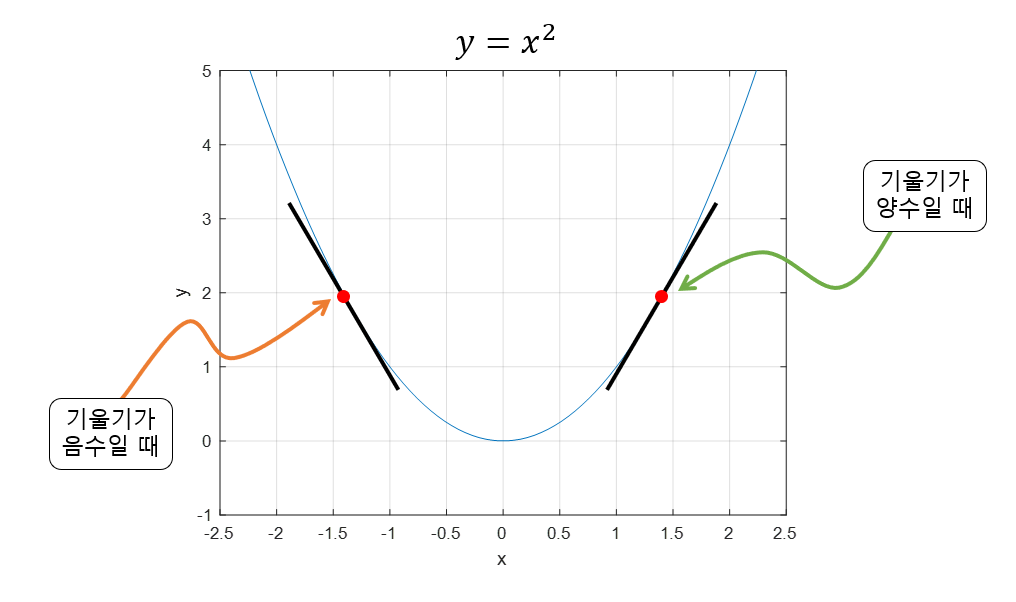
경사하강법은 함수의 기울기(Gradient)를 이용해 함수의 최소값일 때의 x값을 찾기 위한 방법이다
기울기가 양수일 경우 x값이 증가할수록 함수 값도 증가한다
기울기가 음수일 경우 x값이 증가할수록 함수 값은 감소한다
기울기가 가파르다 = 최소값으로부터 거리가 멀다

적절한 크기의 Step Size

적절한 step size 선택은 매우 중요하다. step size가 큰 경우 한 번 이동하는 거리가 커지므로 빠르게 수렴할 수 있지만 과도하게 클 경우 함수값이 계속 커지는, 발산하게 되는 경우가 발생할 수 있다.

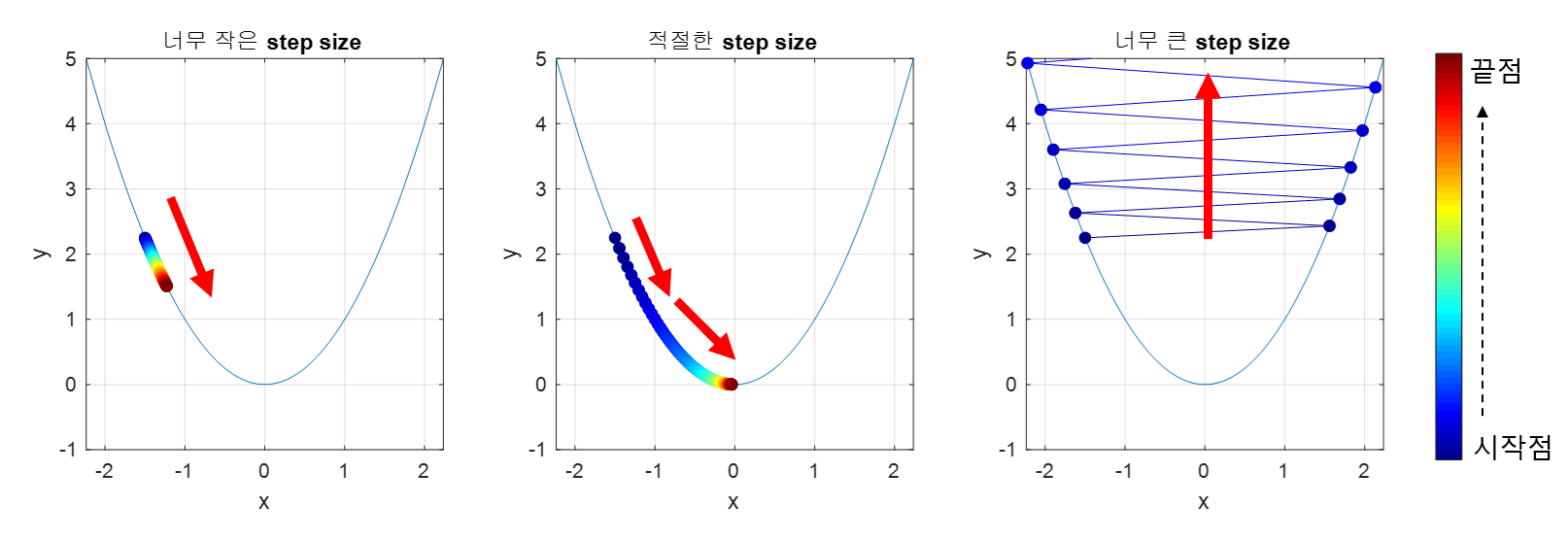
반대로 step size가 너무 작은 경우에는 발산하지는 않지만 최적의 x값을 구하는데 소요되는 시간이 너무 오래 걸리게 된다.

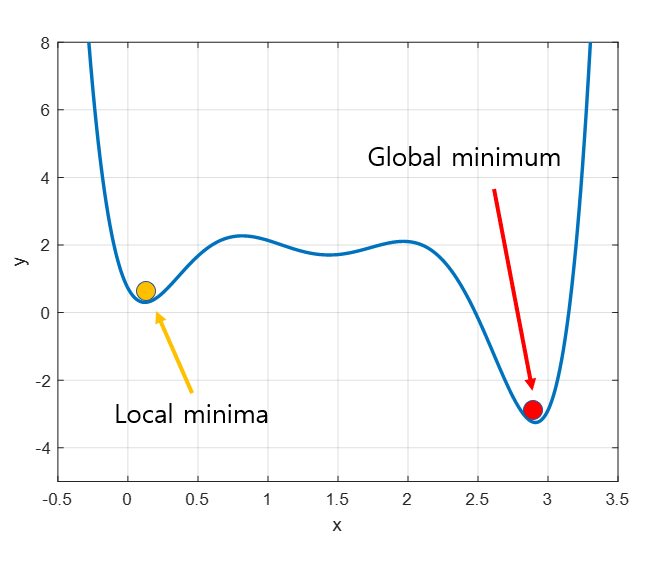
local minima 문제

local minima는 경사하강법에서 알고리즘을 시작하는 위치가 매번 랜덤하기 때문에 발생하는 문제로 local minima 지점을 최적의 값이라고 판단해 빠져나오지 못하는 경우이다