머신러닝의 분류
머신러닝은 인공지능을 구현하는 여러 방법 중 하나로 유용한 함수를 컴퓨터가 학습하는 것이다.
머신러닝은 상황(Task)에 따라 크게 3가지로 분류가 가능하다
1. Supervised Learning (지도 학습)
지도 학습은 이러한 input이 들어오면 이런 output이 나와야 한다는 것을 알려주는 것이다
- Classification 분류
- Regression 회귀
2. Un Supervised Learning (비지도 학습)
컴퓨터 스스로 데이터에 있는 속성들, 특징들을 추출해내는 학습 방법이다
- Clustering 군집화
- Anomaly Detection 이상치 탐지
3. Reinforcement Learning (강화 학습)
정확히 디렉션은 주지 않지만 해당 액션에 대해 리워드를 정보로 줌으로써 학습하는 방법이다
- Markov Decision
- Process
- DQN
- A3C
위 세가지 머신러닝의 분류 중 지도 학습,
그리고 지도 학습 중에서도 분류에 대해 알아보겠다.
1. Supervised Learning (지도 학습)
-
지도 학습은 학습데이터로부터 함수 F를 찾는 방법론이다
(X : 독립변수, 입력변수 / y : 종속변수, 출력변수) -
종속변수 Y가 범주형이면 Classification,
연속형이면 Regression으로 분류한다
0) Bias-Variance Tradeoff
모든 모델은 복잡도를 통제할 수 있는 하이퍼파라미터를 갖고 있다
가장 좋은 성능을 낼 수 있는 모델을 학습하기 위해 최적의 하이퍼파라미터를 결정해야 한다
- 모형의 오차 = Bias(치우침) + Variance(분산)
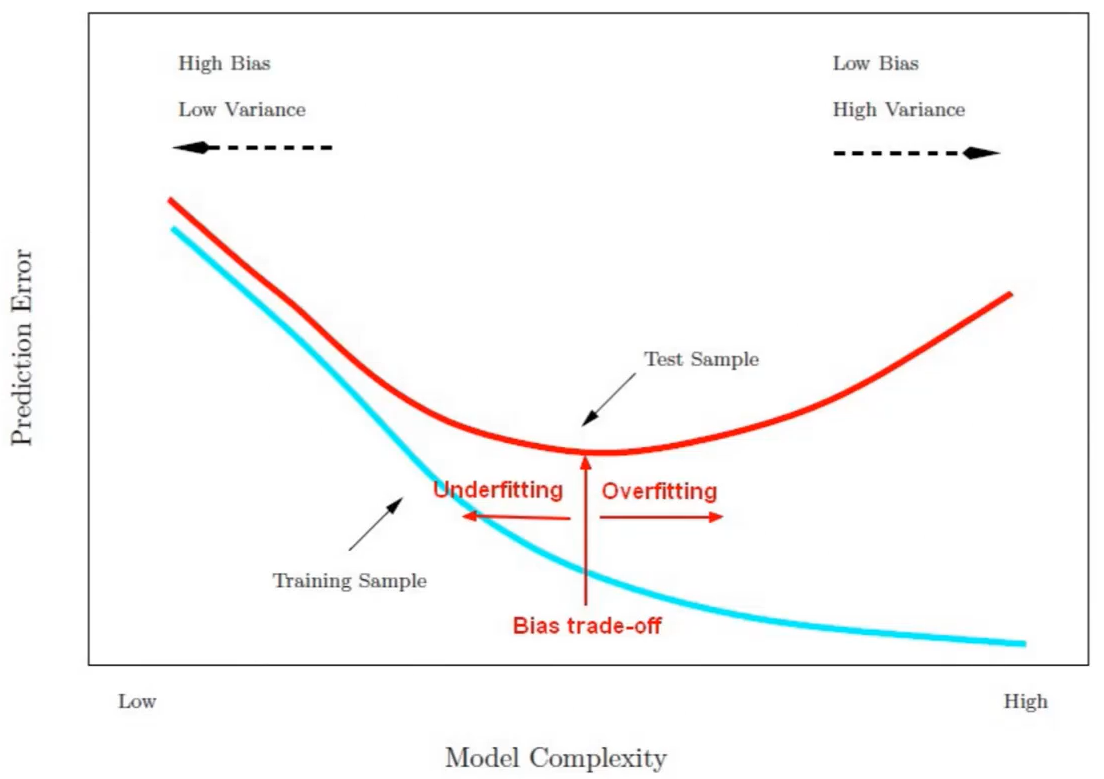
- 모델의 복잡도 ⬆ : Bias ⬇, Variance ⬆ - 복잡도가 너무 높으면 과대적합(overfitting)
- 모델의 복잡도 ⬇ : Bias ⬆, Variance ⬇ - 복잡도가 너무 낮으면 과소적합(underfitting)
1-1) Classification 예시
-
범주형 종속변수 : Class, Label
-
분류 문제 예시
제품이 불량인지 양품인지 분류
고객이 이탈고객인지 잔류고객인지 분류
카드 거래가 정상적인지 사기인지 분류 -
Classification Models
특정 모델이 모든 경우에 대해 항상 좋은 성능을 낸다고 보장할 수 없음
문제상황에 따라 적합한 모델을 선택해야 함
1-2) K-Nearest Neighbors (KNN)
- 간단하지만 널리 활용이 될 만큼 성능이 꽤 괜찮은 모형
“두 관측치의 거리가 가까우면 Y(target or label)도 비슷하다” - K개의 주변 관측치의 Class에 대한 majority voting(다수결)
= 주위 관측치를 보고 가장 다수에 속하는 클래스로 분류해주는 것 - 거리에 기반한 Distance-based model, 개별 instance들에 대해 특성을 공유할 것이라는 가정을 기반에 두기 때문에 instance-based learning 라고 표현하기도 한다
k값에 따라 관측치의 결과값이 달라질 수 있다
K의 영향
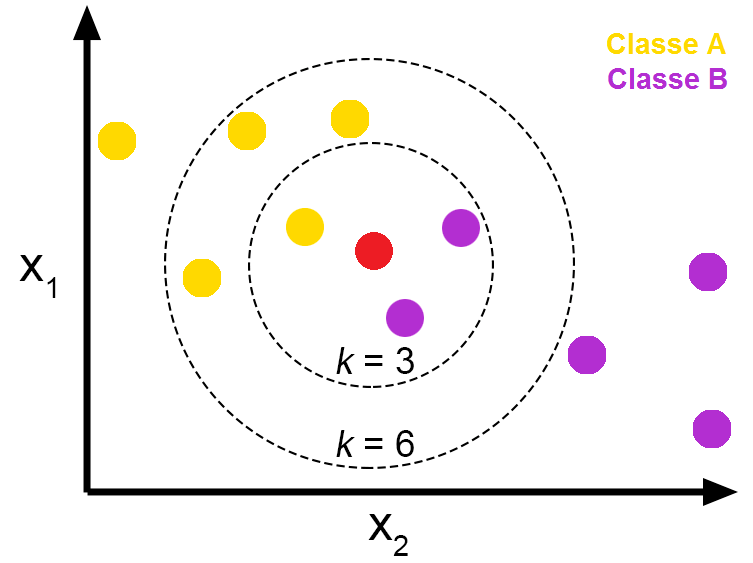
- 위 그림처럼 k에 따라서 분류 결과가 달라진다 = k는 하이퍼파라미터라는 의미
수치형 변수
- 두 점 사이 거리를 계산하여 가까운 순으로 k에 포함시킨다
- 두 관측치 사이의 거리를 측정할 수 있는 방법
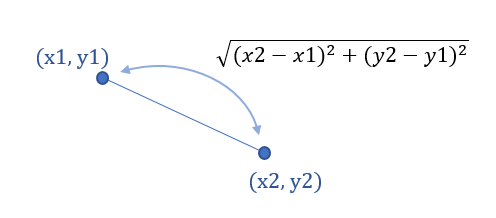
범주형 변수는 Dummy Variable로 변환하여 거리 계산 (원핫인코딩과 같은 방법)
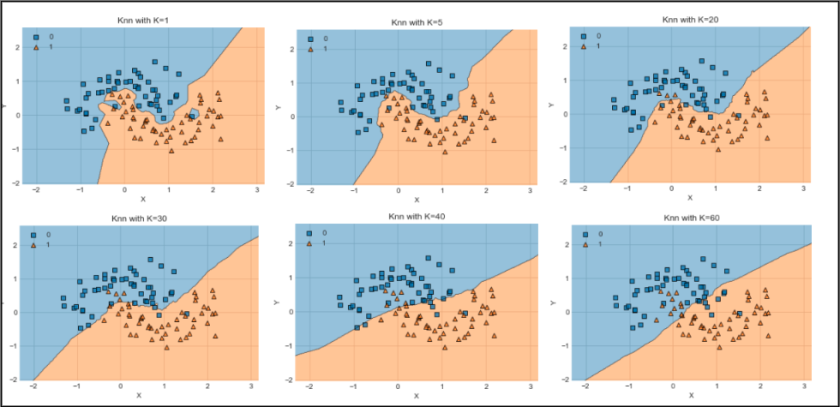
위 그림처럼 K가 클수록 Underfitting / K가 작을수록 Overfitting의 가능성이 있다
1-3) Logistic Regression 다중선형회귀분석
y가 범주형 변수, Classification 태스크에 대해서 해결하는 선형 모형을 Logistic Regression이라고 부른다
범주형 반응변수
- 이진변수(반응변수 값이 0 or 1)
- 멀티변수(반응변수 값이 1 or 2 or 3 이상)
※ 이때는 일반회귀분석과는 다른 방식으로 접근해야 될 필요성이 있다
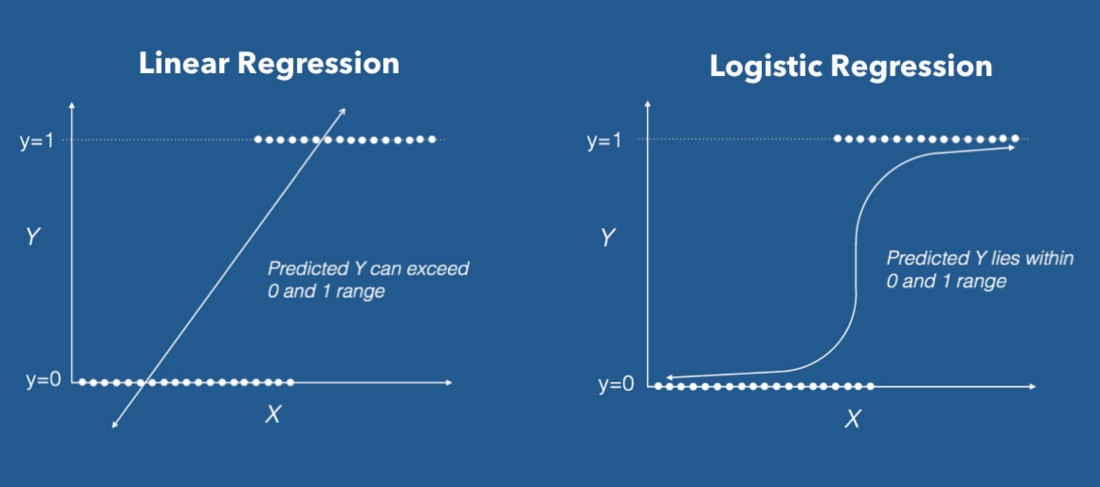
로지스틱 회쉬분석의 필요성
-
로지스틱 회귀분석의 목적
이진형의 형태를 갖는 종속변수에 대해 회귀식의 형태로 모형을 추정하는 것이다 -
왜 회귀식으로 표현해야 하는가?
회귀식으로 표현될 경우 변수의 통계적 유의성 분석 및
종속변수에 미치는 영향력 등을 알 수 있다 -
로지스틱 회귀분석의 특징
1) 종속변수 Y를 그대로 사용하는 것이 아니라 Y에 대한로짓함수(logit function)를 회귀식의 종속변수로 사용한다
2) 로짓함수는 설명변수의 선형결합으로 표현된다
3) 로짓함수의 값은 종속변수에 대한 성공확률로 역산될 수 있어 분류 문제에 적용이 가능하다
Cross-Entropy Loss
-
정의 : 실제값과 어떤 클래스(o or 1 혹은 그 이상 여러개의 클래스가 있을 수 있다)에 속하는 확률값을 cross로 곱해서 모두 더한다음 앞에 마이너스(-)값을 취해준 것
-
목적 : 이것에 따라서 분류가 잘 됐는지 안 됐는지 측정할 수 있다
※ 이 Loss를 minimize 해주게 되면 실제 클래스로 분류될 확률이 최대화가 된다
